20. 판다스 활용: 기초 통계

주요 내용

Series와 DataFrame 객체를로부터 기초 통계 자료를 추출하는 방식을 다룬다.

• 합, 평균, 표준편차

• 상관관계, 공분산

• 중복값 처리

기본 설정

pandas 라이브러리는 보통 pd 라는 별칭으로 사용된다.

import pandas as pd
import numpy as np

랜덤 시드, 어레이 내부에 사용되는 부동소수점 정확도, 도표 크기 지정 옵션 등은 이전과 동일하다.

np.random.seed(12345)
np.set_printoptions(precision=4, suppress=True)

import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))

Series와 DataFrame을 표로 보여줄 때 사용되는 행의 수를 20으로 지정한다. 기본 값은 60이다.

pd.options.display.max_rows # 원래 60이 기본.

60

기본값을 20으로 변경한다.

pd.set_option("display.max_rows", 20)

20.1. 데이터 탐색

데이터 탐색을 위한 주요 메서드를 살펴 본다.

• head()

• tail()

• info()

설명을 위해 아래 데이터프레임을 이용한다.

dict = {'state': ['Ohio', 'Ohio', 'Ohio', 'Nevada', 'Nevada', 'Nevada', 'NY', 'NY', 'NY'],
         'year': [str(num) for num in [2000, 2001, 2002, 2001, 2002, 2003, 2002, 2003, 2004]],
         'pop': [1.5, 1.7, 3.6, 2.4, 2.9, 3.2, 8.3, 8.4, 8.5],
         'debt':np.linspace(0, 1, 9)}

frame = pd.DataFrame(dict, columns=['year', 'state', 'pop', 'debt'],
                      index=['one', 'two', 'three', 'four',
                             'five', 'six', 'seven', 'eight', 'nine'])
frame

	year	state	pop	debt
one	2000	Ohio	1.5	0.000
two	2001	Ohio	1.7	0.125
three	2002	Ohio	3.6	0.250
four	2001	Nevada	2.4	0.375
five	2002	Nevada	2.9	0.500
six	2003	Nevada	3.2	0.625
seven	2002	NY	8.3	0.750
eight	2003	NY	8.4	0.875
nine	2004	NY	8.5	1.000

head() 메서드

head() 메서드는 지정된 크기만큼의 행을 보여준다. 인자를 지정하지 않으면 처음 5개의 행을 보여준다.

frame.head(3)

	year	state	pop	debt
one	2000	Ohio	1.5	0.000
two	2001	Ohio	1.7	0.125
three	2002	Ohio	3.6	0.250

frame.head()

	year	state	pop	debt
one	2000	Ohio	1.5	0.000
two	2001	Ohio	1.7	0.125
three	2002	Ohio	3.6	0.250
four	2001	Nevada	2.4	0.375
five	2002	Nevada	2.9	0.500

tail() 메서드

tail() 메서드는 지정된 크기만큼의 행을 뒤에서부터 보여준다. 인자를 지정하지 않으면 뒤에서부터 5개의 행을 보여준다.

frame.tail(3)

	year	state	pop	debt
seven	2002	NY	8.3	0.750
eight	2003	NY	8.4	0.875
nine	2004	NY	8.5	1.000

frame.tail()

	year	state	pop	debt
five	2002	Nevada	2.9	0.500
six	2003	Nevada	3.2	0.625
seven	2002	NY	8.3	0.750
eight	2003	NY	8.4	0.875
nine	2004	NY	8.5	1.000

info() 메서드

열(columns) 별로 결측치가 아닌 항목의 수와 자료형을 확인해준다.

• 9 non-null: 결측치가 아닌 항목이 9개 있음을 의미함.

• object: 일반적으로 문자열 자료형을 가리킴.

frame.info()

<class 'pandas.core.frame.DataFrame'>
Index: 9 entries, one to nine
Data columns (total 4 columns):
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   year    9 non-null      object 
 1   state   9 non-null      object 
 2   pop     9 non-null      float64
 3   debt    9 non-null      float64
dtypes: float64(2), object(2)
memory usage: 360.0+ bytes

20.2. 합, 평균, 표준편차

기초 통계에서 사용되는 주요 메서드들의 활용법을 살펴본다.

• sum()

• mean()

• std()

• idxmax()/idxmin()

• cumsum()

• describe()

기본적으로 열 단위로 작동하며, 결측치는 행 또는 열의 모든 값이 결측치가 아니라면 기본적으로 무시된다. 행 단위로 작동하게 하려면 축을 axis=1 또는 axis='columns로 지정하고, 결측치를 무시하지 않으려면 skipna=False로 지정한다.

df = pd.DataFrame([[1.4, np.nan], [7.1, -4.5],
                   [np.nan, np.nan], [0.75, -1.3]],
                  index=['a', 'b', 'c', 'd'],
                  columns=['one', 'two'])
df

	one	two
a	1.40	NaN
b	7.10	-4.5
c	NaN	NaN
d	0.75	-1.3

• sum() 메서드: 행/열 단위 합 계산

df.sum()

one    9.25
two   -5.80
dtype: float64

결측치를 무시하지 않으면, 결측치가 포함된 행/렬에 대한 계산은 하지 않는다.

df.sum(skipna=False)

one   NaN
two   NaN
dtype: float64

df.sum(axis='columns')

a    1.40
b    2.60
c    0.00
d   -0.55
dtype: float64

시리즈는 하나의 열을 갖는 데이터프레임처럼 작동한다.

df['one']

a    1.40
b    7.10
c     NaN
d    0.75
Name: one, dtype: float64

df['one'].sum()

9.25

• mean() 메서드: 평균값 계산

df.mean()

one    3.083333
two   -2.900000
dtype: float64

df.mean(axis='columns')

a    1.400
b    1.300
c      NaN
d   -0.275
dtype: float64

결측치를 무시하지 않으면, 결측치가 포함된 행/렬에 대한 계산은 하지 않는다.

df.mean(skipna=False)

one   NaN
two   NaN
dtype: float64

df.mean(axis='columns', skipna=False)

a      NaN
b    1.300
c      NaN
d   -0.275
dtype: float64

시리즈의 경우도 동일하게 작동한다.

df['one'].mean()

3.0833333333333335

df['one'].mean(skipna=False)

nan

• std() 메서드: 표준편차 계산

df.std()

one    3.493685
two    2.262742
dtype: float64

df.std(axis='columns')

a         NaN
b    8.202439
c         NaN
d    1.449569
dtype: float64

df.std(skipna=False)

one   NaN
two   NaN
dtype: float64

df.std(axis='columns', skipna=False)

a         NaN
b    8.202439
c         NaN
d    1.449569
dtype: float64

• idxmax()/idxmin(): 최댓값/최솟값을 갖는 인덱스 확인

아래 코드는 열별 최댓값을 갖는 인덱스를 찾아준다.

df.idxmax()

one    b
two    d
dtype: object

• cumsum(): 누적 합 계산

df.cumsum()

	one	two
a	1.40	NaN
b	8.50	-4.5
c	NaN	NaN
d	9.25	-5.8

df.cumsum(skipna=False)

	one	two
a	1.4	NaN
b	8.5	NaN
c	NaN	NaN
d	NaN	NaN

• describe(): 요약 통계 보여주기

수치형 데이터의 경우 평균값, 표준편차, 사분위수 등의 통계 정보를 요약해서 보여준다.

df.describe()

	one	two
count	3.000000	2.000000
mean	3.083333	-2.900000
std	3.493685	2.262742
min	0.750000	-4.500000
25%	1.075000	-3.700000
50%	1.400000	-2.900000
75%	4.250000	-2.100000
max	7.100000	-1.300000

20.3. 상관관계와 공분산

금융 사이트에서 구한 4 개 회사의 주가(price)와 거래량(volume)을 담고 있는 두 개의 데이터를 이용하여 상관계수와 공분산을 계산해본다. 이를 위해 먼저 바이너리 파일 두 개를 다운로드해서 지정된 하위 디렉토리에 저장한다.

• 파일 저장 디렉토리 지정 및 생성

from pathlib import Path

data_path = Path() / "examples"

data_path.mkdir(parents=True, exist_ok=True)

• 특정 서버에서 파일 다운로드 함수

import requests

# 파일 서버 기본 주소
base_url = "https://raw.githubusercontent.com/codingalzi/datapy/master/jupyter-book/examples/"
    
def myWget(filename):
    # 다운로드 대상 파일 경로
    file_url = base_url + filename
    
    # 저장 경로와 파일명
    target_path = data_path / filename

    data = requests.get(file_url)
    
    with open(target_path, 'wb') as f:
        f.write(data.content)

두 개의 픽클 파일 다운로드한다.

• pkl 파일: 판다스에서 제공하는 객체를 to_pickle() 메서드를 이용하여 컴퓨터에 파일로 저장할 때 사용되는 바이너리 파일.

myWget("yahoo_price.pkl")

myWget("yahoo_volume.pkl")

다운로드한 두 개의 데이터를 불러온다.

• read_pickle(): 저장된 pkl 파일을 파이썬으로 불러오는 함수

아래 코드는 일별 주가 데이터를 불러온다. 2010년 1월 4일부터 2016년 10월 21일까지의 데이터 1714개를 담고 있다.

price = pd.read_pickle('examples/yahoo_price.pkl')
price

	AAPL	GOOG	IBM	MSFT
Date
2010-01-04	27.990226	313.062468	113.304536	25.884104
2010-01-05	28.038618	311.683844	111.935822	25.892466
2010-01-06	27.592626	303.826685	111.208683	25.733566
2010-01-07	27.541619	296.753749	110.823732	25.465944
2010-01-08	27.724725	300.709808	111.935822	25.641571
...	...	...	...	...
2016-10-17	117.550003	779.960022	154.770004	57.220001
2016-10-18	117.470001	795.260010	150.720001	57.660000
2016-10-19	117.120003	801.500000	151.259995	57.529999
2016-10-20	117.059998	796.969971	151.520004	57.250000
2016-10-21	116.599998	799.369995	149.630005	59.660000

1714 rows × 4 columns

아래 코드는 동일 회사, 동일 날짜의 1일 거래량(volume) 담고 있는 데이터를 불러온다.

volume = pd.read_pickle('examples/yahoo_volume.pkl')
volume

	AAPL	GOOG	IBM	MSFT
Date
2010-01-04	123432400	3927000	6155300	38409100
2010-01-05	150476200	6031900	6841400	49749600
2010-01-06	138040000	7987100	5605300	58182400
2010-01-07	119282800	12876600	5840600	50559700
2010-01-08	111902700	9483900	4197200	51197400
...	...	...	...	...
2016-10-17	23624900	1089500	5890400	23830000
2016-10-18	24553500	1995600	12770600	19149500
2016-10-19	20034600	116600	4632900	22878400
2016-10-20	24125800	1734200	4023100	49455600
2016-10-21	22384800	1260500	4401900	79974200

1714 rows × 4 columns

주가의 일단위 변화율을 알아보기 위해 퍼센트 변화율을 확인해보자.

참고: 증권분야에서 return은 이익율을 의미한다.

returns = price.pct_change()
returns.tail()

	AAPL	GOOG	IBM	MSFT
Date
2016-10-17	-0.000680	0.001837	0.002072	-0.003483
2016-10-18	-0.000681	0.019616	-0.026168	0.007690
2016-10-19	-0.002979	0.007846	0.003583	-0.002255
2016-10-20	-0.000512	-0.005652	0.001719	-0.004867
2016-10-21	-0.003930	0.003011	-0.012474	0.042096

corr()/cov() 메서드

상관계수와 공분산 모두 두 확률변수 사이의 선형관계를 보여주며 차이점은 다음과 같다.

• 공분산: 두 확률변수 \(X, Y\) 사이의 선형관계를 계량화 함. 양수/음수 여부에 따라 양 또는 음의 선형관계이며, 절댓값이 클 수록 강한 선형관계임. 다만, 사용되는 확률변수의 척도(scale)에 많은 영향을 받음. 따라서 보통 정규화한 값인 상관계수를 사용함.

\[\begin{split} \begin{align*} Cov(X, Y) & = E((X-\mu_X)(Y-\mu_Y))\\[2ex] \mu_X & = E(X) = \dfrac{\sum X}{n}\\[1.5ex] \mu_Y & = E(Y) = \dfrac{\sum Y}{n} \end{align*} \end{split}\]

• 상관계수: 두 확률변수 사이의 선형관계를 -1과 1 사이의 값으로 표현. 양수/음수 여부에 따라 양 또는 음의 선형관계이며, 절댓값이 1에 가까울 수록 강한 선형관계임.

\[\begin{split} \begin{align*} \rho & = \frac{Cov(X, Y)}{\sigma_X\cdot \sigma_Y}\\[2ex] \sigma_X & = \sqrt{Var(X)}\\[1.5ex] \sigma_X & = \sqrt{Var(X)}\\[1.5ex] Var(X) & = \dfrac{\sum (X-\mu_X)^2}{n}\\[1.5ex] Var(Y) & = \dfrac{\sum (X-\mu_Y)^2}{n} \end{align*} \end{split}\]

‘MSFT’와 ‘IBM’ 사이의 상관계수는 다음과 같다.

returns['MSFT'].corr(returns['IBM'])

0.49976361144151144

‘MSFT’와 ‘IBM’ 사이의 공분산은 다음과 같다.

returns['MSFT'].cov(returns['IBM'])

8.870655479703546e-05

전체 회사를 대상으로 하는 상관계수와 공분산을 계산할 수도 있다.

returns.corr()

	AAPL	GOOG	IBM	MSFT
AAPL	1.000000	0.407919	0.386817	0.389695
GOOG	0.407919	1.000000	0.405099	0.465919
IBM	0.386817	0.405099	1.000000	0.499764
MSFT	0.389695	0.465919	0.499764	1.000000

returns.cov()

	AAPL	GOOG	IBM	MSFT
AAPL	0.000277	0.000107	0.000078	0.000095
GOOG	0.000107	0.000251	0.000078	0.000108
IBM	0.000078	0.000078	0.000146	0.000089
MSFT	0.000095	0.000108	0.000089	0.000215

20.4. 중복과 빈도

unique() 메서드

시리즈에서 사용된 값을 중복 없이 확인하려면 unique() 메서드를 이용한다. set() 함수와 유사하게 작동하며, 넘파이 어레이를 반환한다.

obj = pd.Series(['c', 'a', 'd', 'a', 'a', 'b', 'b', 'c', 'c'])
obj

0    c
1    a
2    d
3    a
4    a
5    b
6    b
7    c
8    c
dtype: object

uniques = obj.unique()
uniques

array(['c', 'a', 'd', 'b'], dtype=object)

value_counts() 메서드

값들의 빈도수를 확인하기 위해 사용한다.

obj.value_counts()

c    3
a    3
b    2
d    1
Name: count, dtype: int64

20.5. 실전 예제: 붓꽃 데이터셋 분석

아래 링크에 아이리스(붓꽃) 데이터(iris.data)가 저장되어 있다.

url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'

iris.data 파일에는 아래 형식의 데이터가 150개 들어 있다.

5.1,3.5,1.4,0.2,Iris-setosa
4.9,3.0,1.4,0.2,Iris-setosa
4.7,3.2,1.3,0.2,Iris-setosa
4.6,3.1,1.5,0.2,Iris-setosa
5.0,3.6,1.4,0.2,Iris-setosa
...

포함된 데이터 특성들 사이의 구분자, 즉 열 구분자는 쉼표가 사용되었으며 각 열의 라벨은 지정되어 있지 않다. 따라서 판다스의 read_csv() 함수의 인자를 아래처럼 지정해서 해당 파일을 데이터프레임으로 불러온다.

iris = pd.read_csv(url, sep=',', header=None)
iris

	0	1	2	3	4
0	5.1	3.5	1.4	0.2	Iris-setosa
1	4.9	3.0	1.4	0.2	Iris-setosa
2	4.7	3.2	1.3	0.2	Iris-setosa
3	4.6	3.1	1.5	0.2	Iris-setosa
4	5.0	3.6	1.4	0.2	Iris-setosa
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	Iris-virginica
146	6.3	2.5	5.0	1.9	Iris-virginica
147	6.5	3.0	5.2	2.0	Iris-virginica
148	6.2	3.4	5.4	2.3	Iris-virginica
149	5.9	3.0	5.1	1.8	Iris-virginica

150 rows × 5 columns

하나의 데이터에 사용된 값들은 하나의 아이리스(붓꽃)에 대한 꽃잎, 꽃받침과 관련된 특성(features)과 품종을 나타내며, 보다 구체적으로 아래 순서를 따른다.

꽃받침 길이, 꽃받침 너비, 꽃잎 길이, 꽃잎 너비, 품종

열 라벨을 언급한대로 수정한다.

columns = ['꽃받침길이', '꽃받침너비', '꽃잎길이', '꽃잎너비', '품종']

열 라벨의 영문명은 다음과 같다.

columns_eng = ['Sepal length', 'Sepal width', 'Petal length', 'Petal width', 'Variety']

열 라벨을 한글명으로 지정해보자.

iris.columns = columns
iris

	꽃받침길이	꽃받침너비	꽃잎길이	꽃잎너비	품종
0	5.1	3.5	1.4	0.2	Iris-setosa
1	4.9	3.0	1.4	0.2	Iris-setosa
2	4.7	3.2	1.3	0.2	Iris-setosa
3	4.6	3.1	1.5	0.2	Iris-setosa
4	5.0	3.6	1.4	0.2	Iris-setosa
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	Iris-virginica
146	6.3	2.5	5.0	1.9	Iris-virginica
147	6.5	3.0	5.2	2.0	Iris-virginica
148	6.2	3.4	5.4	2.3	Iris-virginica
149	5.9	3.0	5.1	1.8	Iris-virginica

150 rows × 5 columns

포함된 5개의 특성(열)별 정보는 다음과 같다.

iris.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 150 entries, 0 to 149
Data columns (total 5 columns):
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   꽃받침길이   150 non-null    float64
 1   꽃받침너비   150 non-null    float64
 2   꽃잎길이    150 non-null    float64
 3   꽃잎너비    150 non-null    float64
 4   품종      150 non-null    object 
dtypes: float64(4), object(1)
memory usage: 6.0+ KB

수치형 특성들의 간략한 통계 정보는 다음과 같다. 즉 품종 특성은 제외된다.

iris.describe()

	꽃받침길이	꽃받침너비	꽃잎길이	꽃잎너비
count	150.000000	150.000000	150.000000	150.000000
mean	5.843333	3.054000	3.758667	1.198667
std	0.828066	0.433594	1.764420	0.763161
min	4.300000	2.000000	1.000000	0.100000
25%	5.100000	2.800000	1.600000	0.300000
50%	5.800000	3.000000	4.350000	1.300000
75%	6.400000	3.300000	5.100000	1.800000
max	7.900000	4.400000	6.900000	2.500000

수치형 특성 각각의 의미는 아래 사진에서 확인할 수 있다.

품종 확인

품종은 다음과 같이 확인된다.

varieties = iris.품종.unique()
varieties

array(['Iris-setosa', 'Iris-versicolor', 'Iris-virginica'], dtype=object)

150개의 데이터는 아래 세 개의 품종으로 구분된다.

'Iris-setosa', 'Iris-versicolor', 'Iris-virginica'

품종별로 각각 50개의 데이터 샘플이 포함되어 있다.

iris.품종.value_counts()

품종
Iris-setosa        50
Iris-versicolor    50
Iris-virginica     50
Name: count, dtype: int64

품종명을 단순화시키기 위해 유니버설 함수를 정의한다.

shortening = np.vectorize(lambda x: x.replace('Iris-', '').capitalize())

shortening() 함수는 Iris- 접두사를 제거한 후에 대문자로 시작하는 품종명을 생성한다.

varieties = shortening(varieties)
varieties

array(['Setosa', 'Versicolor', 'Virginica'], dtype='<U10')

품종을 문자열이 아닌 0, 1, 2로 구분하면 데이터프레임을 보다 유용하게 활용할 수 있다. 이를 위해 아래 사전을 이용한다.

varieties_dict = {item[1]:item[0] for item in enumerate(iris.품종.unique())}
varieties_dict

{'Iris-setosa': 0, 'Iris-versicolor': 1, 'Iris-virginica': 2}

map() 메서드를 이용하여 품종을 0, 1, 2로 변환한다.

iris.loc[:, '품종'] = iris.품종.map(lambda x: varieties_dict[x])

iris

	꽃받침길이	꽃받침너비	꽃잎길이	꽃잎너비	품종
0	5.1	3.5	1.4	0.2	0
1	4.9	3.0	1.4	0.2	0
2	4.7	3.2	1.3	0.2	0
3	4.6	3.1	1.5	0.2	0
4	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	2
146	6.3	2.5	5.0	1.9	2
147	6.5	3.0	5.2	2.0	2
148	6.2	3.4	5.4	2.3	2
149	5.9	3.0	5.1	1.8	2

150 rows × 5 columns

산점도

아래 코드는 꽃받침의 길이와 너비를 이용한 산점도를 그린다.

import matplotlib.pyplot as plt

scatter = plt.scatter(iris.iloc[:, 0], iris.iloc[:, 1], c=iris.iloc[:, 4])
plt.xlabel(columns_eng[0])
plt.ylabel(columns_eng[1])

handles, colors = scatter.legend_elements()

plt.legend(handles, colors)
plt.show()

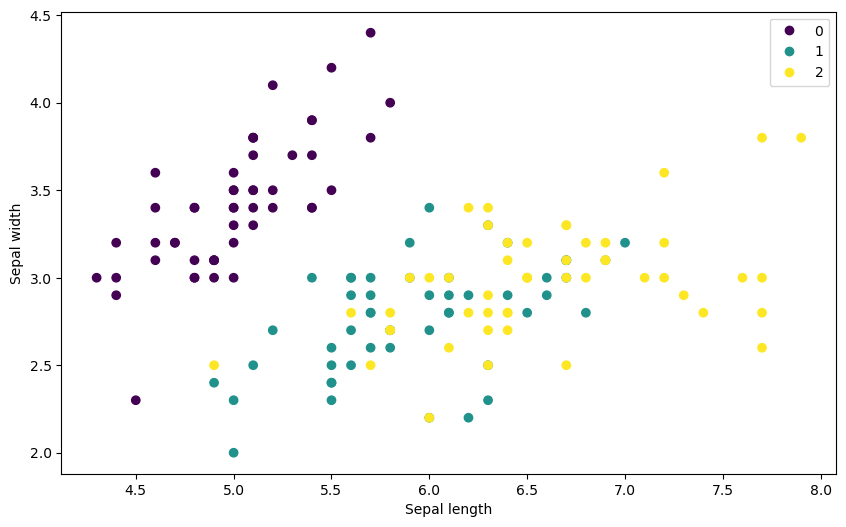
범례에 사용되는 라벨을 숫자가 아닌 품종명으로 변경하려면 다음과 같이 varieties를 이용한다.

import matplotlib.pyplot as plt

scatter = plt.scatter(iris.iloc[:, 0], iris.iloc[:, 1], c=iris.iloc[:, 4])
plt.xlabel(columns_eng[0])
plt.ylabel(columns_eng[1])

handles, _ = scatter.legend_elements()

plt.legend(handles, varieties)
plt.show()

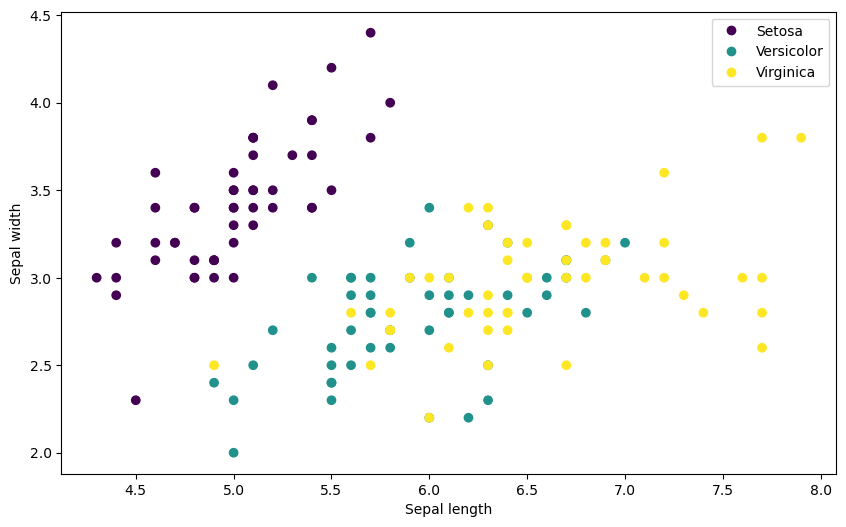
반면에 아래 코드는 꽃잎의 길이와 너비를 이용한 산점도를 그린다.

import matplotlib.pyplot as plt

scatter = plt.scatter(iris.iloc[:, 2], iris.iloc[:, 3], c=iris.iloc[:, 4])
plt.xlabel(columns_eng[2])
plt.ylabel(columns_eng[3])

handles, _ = scatter.legend_elements()

plt.legend(handles, varieties)
plt.show()

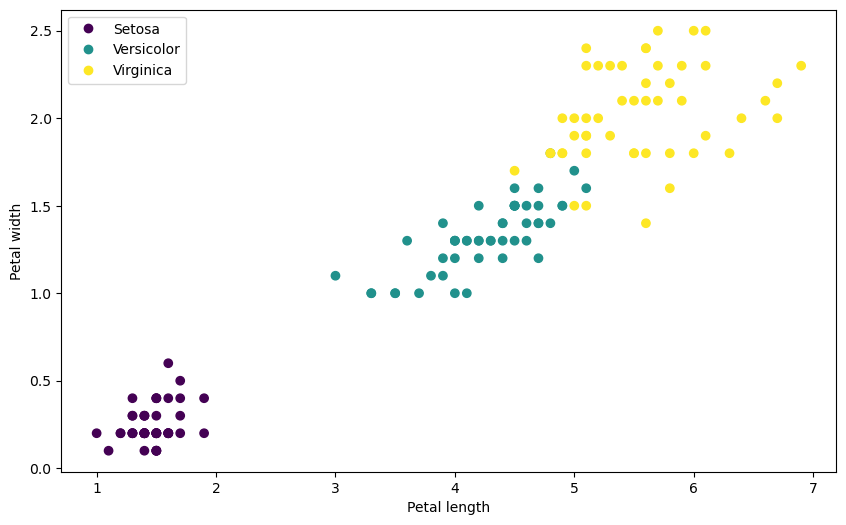
예제 1

꽃받침 길이(0번 열)와 꽃잎 길이(2번 열) 사이의 피어슨 상관계수를 계산하라.

답:

데이터프레임의 corr() 메서드는 모든 특성들 사이의 피어슨 상관계수로 이루어진 데이터프레임을 반환환다.

iris_corr = iris.iloc[:, :4].corr()
iris_corr

	꽃받침길이	꽃받침너비	꽃잎길이	꽃잎너비
꽃받침길이	1.000000	-0.109369	0.871754	0.817954
꽃받침너비	-0.109369	1.000000	-0.420516	-0.356544
꽃잎길이	0.871754	-0.420516	1.000000	0.962757
꽃잎너비	0.817954	-0.356544	0.962757	1.000000

따라서 ‘꽃받침길이’와 다른 특성들 사이의 상관계수를 역순으로 정렬하면 다음과 같다.

iris_corr['꽃받침길이'].sort_values(ascending=False)

꽃받침길이    1.000000
꽃잎길이     0.871754
꽃잎너비     0.817954
꽃받침너비   -0.109369
Name: 꽃받침길이, dtype: float64

따라서 ‘꽃받침길이’와 ‘꽃잎길이’ 사이의 상관계수가 가장 높다.

예제 2

버시컬러 품종에 해당하는 데이터만 iris로부터 추출하라.

답:

버시컬러 품종은 1에 해당하기에 다음 부울 마스크를 이용한다.

mask = iris.iloc[:, -1] == 1
mask

0      False
1      False
2      False
3      False
4      False
       ...  
145    False
146    False
147    False
148    False
149    False
Name: 품종, Length: 150, dtype: bool

iris_versicolor = iris[mask]
iris_versicolor

	꽃받침길이	꽃받침너비	꽃잎길이	꽃잎너비	품종
50	7.0	3.2	4.7	1.4	1
51	6.4	3.2	4.5	1.5	1
52	6.9	3.1	4.9	1.5	1
53	5.5	2.3	4.0	1.3	1
54	6.5	2.8	4.6	1.5	1
...	...	...	...	...	...
95	5.7	3.0	4.2	1.2	1
96	5.7	2.9	4.2	1.3	1
97	6.2	2.9	4.3	1.3	1
98	5.1	2.5	3.0	1.1	1
99	5.7	2.8	4.1	1.3	1

50 rows × 5 columns

예제 3

각 특성별 평균값, 중위수, 표준편차를 구하라.

답:

수치형 데이터의 평균값, 중위수, 표준편차는 describe() 메서드로 확인된다. 중위수는 50% 라벨의 행에 위치한다.

iris.describe()

	꽃받침길이	꽃받침너비	꽃잎길이	꽃잎너비
count	150.000000	150.000000	150.000000	150.000000
mean	5.843333	3.054000	3.758667	1.198667
std	0.828066	0.433594	1.764420	0.763161
min	4.300000	2.000000	1.000000	0.100000
25%	5.100000	2.800000	1.600000	0.300000
50%	5.800000	3.000000	4.350000	1.300000
75%	6.400000	3.300000	5.100000	1.800000
max	7.900000	4.400000	6.900000	2.500000

예제 4

세 개의 품종 각각에 대해 꽃받침너비(1번 열)의 평균값을 계산하여 아래 모양의
시리즈(Series)를 가리키는 iris_mean_sepal_width 변수를 선언하라.

Iris-setosa	3.418
Iris-versicolor	2.770
Iris-virginica	2.974

답:

아래 코드는 품종별로 꽃받침너비의 평균값을 계산해서 리스트에 추가한다.

iris_mean_sepal_width = []

for variety in range(3):
    mask = iris.iloc[:, 4] == variety
    mean_0 = iris[mask]['꽃받침너비'].mean()
    iris_mean_sepal_width.append(mean_0)

시리즈 생성을 위해 index와 name 키워드를 인자를 지정한다.

iris_mean_sepal_width = pd.Series(iris_mean_sepal_width, index=varieties, name='평균꽃받침너비')
iris_mean_sepal_width

Setosa        3.418
Versicolor    2.770
Virginica     2.974
Name: 평균꽃받침너비, dtype: float64

예제 5

iris에 포함된 모든 수치형 특성을 정규화normalization를 이용하여 모두 0과 1사이의 값으로 변환하라.

힌트: 정규화에 대한 설명은 정규화/표준화을 참고하라.

답:

수치형 특성만을 가리키는 iris_features를 선언한다.

iris_features = iris.iloc[:, :4]
iris_features

	꽃받침길이	꽃받침너비	꽃잎길이	꽃잎너비
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2
4	5.0	3.6	1.4	0.2
...	...	...	...	...
145	6.7	3.0	5.2	2.3
146	6.3	2.5	5.0	1.9
147	6.5	3.0	5.2	2.0
148	6.2	3.4	5.4	2.3
149	5.9	3.0	5.1	1.8

150 rows × 4 columns

아니면 다음과 같이 drop() 메서드를 이용할 수도 있다.

iris_features = iris.drop('품종', axis=1)
iris_features

	꽃받침길이	꽃받침너비	꽃잎길이	꽃잎너비
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2
4	5.0	3.6	1.4	0.2
...	...	...	...	...
145	6.7	3.0	5.2	2.3
146	6.3	2.5	5.0	1.9
147	6.5	3.0	5.2	2.0
148	6.2	3.4	5.4	2.3
149	5.9	3.0	5.1	1.8

150 rows × 4 columns

min(), max() 등의 데이터프레임 메서드는 기본적으로 축을 0으로 지정해서 열 단위로 작동한다.

iris_features.min()

꽃받침길이    4.3
꽃받침너비    2.0
꽃잎길이     1.0
꽃잎너비     0.1
dtype: float64

iris_features.min(axis=0)

꽃받침길이    4.3
꽃받침너비    2.0
꽃잎길이     1.0
꽃잎너비     0.1
dtype: float64

사칙연산을 활용하여 열별로 정규화된 데이터프레임을 다음과 같이 생성한다.

iris_normalized = (iris_features - iris_features.min())/(iris_features.max() - iris_features.min())

iris_normalized

	꽃받침길이	꽃받침너비	꽃잎길이	꽃잎너비
0	0.222222	0.625000	0.067797	0.041667
1	0.166667	0.416667	0.067797	0.041667
2	0.111111	0.500000	0.050847	0.041667
3	0.083333	0.458333	0.084746	0.041667
4	0.194444	0.666667	0.067797	0.041667
...	...	...	...	...
145	0.666667	0.416667	0.711864	0.916667
146	0.555556	0.208333	0.677966	0.750000
147	0.611111	0.416667	0.711864	0.791667
148	0.527778	0.583333	0.745763	0.916667
149	0.444444	0.416667	0.694915	0.708333

150 rows × 4 columns

예제 6

iris에 사용된 모든 값을 특성 별로 표준화standardization하라.

힌트: 표준화에 대한 설명은 정규화/표준화을 참고하라.

답:

mean(), std() 메서드 또한 열별로 계산된다.

iris_features.mean()

꽃받침길이    5.843333
꽃받침너비    3.054000
꽃잎길이     3.758667
꽃잎너비     1.198667
dtype: float64

iris_features.std()

꽃받침길이    0.828066
꽃받침너비    0.433594
꽃잎길이     1.764420
꽃잎너비     0.763161
dtype: float64

사칙연산을 활용하여 열별로 표준화된 데이터프레임을 다음과 같이 생성한다.

iris_standardized = (iris_features - iris_features.mean()) / iris_features.std()

iris_standardized[:5]

	꽃받침길이	꽃받침너비	꽃잎길이	꽃잎너비
0	-0.897674	1.028611	-1.336794	-1.308593
1	-1.139200	-0.124540	-1.336794	-1.308593
2	-1.380727	0.336720	-1.393470	-1.308593
3	-1.501490	0.106090	-1.280118	-1.308593
4	-1.018437	1.259242	-1.336794	-1.308593

20.6. 연습문제

참고: (실습) 판다스 활용: 통계 기초