캘리포니아 주택 가격

30. 캘리포니아 주택 가격#

넘파이와 판다스 기본 설정

import numpy as np
import pandas as pd

np.set_printoptions(precision=6, suppress=True)
PREVIOUS_MAX_ROWS = pd.options.display.max_rows # 원래 60이 기본.
pd.options.display.max_rows = 20

import matplotlib.pyplot as plt

30.1. 캘리포니아 데이터셋#

1990년대 초에 캘리포니아 주를 20640 개 구역으로 쪼갠 후 구역별로 통계 자료를 조사한 데이터셋이다.

구역별로 다음 10개 내용을 조사했다.

특성	의미
`'longitude'`	위도
`'latitude'`	경도
`'housing_median_age'`	건축물 중위연령
`'total_rooms'`	방의 총 개수
`'total_bedrooms'`	침실 총 개수
`'population'`	인구
`'households'`	가구수
`'median_income'`	중위소득
`'median_house_value'`	주택 중위가격
`'ocean_proximity'`	해안 근접도

30.1.1. 캘리포니아 데이터셋 다운로드#

아래 주소에 tgz 압축 파일로 저장되어 있다. 해당 파일을 다운로드해서 특정 폴더에 저장한 후에 압축을 풀면 csv 파일이 생성되며, 이를 데이터프레임으로 불러온다.

아래 load_housing_data() 함수가 이 과정을 모두 처리한다.

from pathlib import Path
import pandas as pd
import tarfile
import urllib.request

def load_housing_data():
    tarball_path = Path("datasets/housing.tgz")                      # 파일 저장 경로. 파일명 함께 지정.
    if not tarball_path.is_file():                                   # 아직 다운로드하지 않은 경우
        Path("datasets").mkdir(parents=True, exist_ok=True)          # 폴더 생성
        url = "https://github.com/ageron/data/raw/main/housing.tgz"  # 파일 다운로드
        urllib.request.urlretrieve(url, tarball_path)
        with tarfile.open(tarball_path) as housing_tarball:          # tgz 파일 압축 풀기
            housing_tarball.extractall(path="datasets")
    return pd.read_csv(Path("datasets/housing/housing.csv"))         # 압축 풀린 csv 파일 불러오기

데이터셋 다운로드 후 데이터프레임으로 적재한다.

housing = load_housing_data()

30.1.2. 데이터셋 기본 정보 확인#

총 20640개의 데이터 샘플이 포함되며, 10개의 특성(열)을 포함한다.

housing.shape

(20640, 10)

housing

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value	ocean_proximity
0	-122.23	37.88	41.0	880.0	129.0	322.0	126.0	8.3252	452600.0	NEAR BAY
1	-122.22	37.86	21.0	7099.0	1106.0	2401.0	1138.0	8.3014	358500.0	NEAR BAY
2	-122.24	37.85	52.0	1467.0	190.0	496.0	177.0	7.2574	352100.0	NEAR BAY
3	-122.25	37.85	52.0	1274.0	235.0	558.0	219.0	5.6431	341300.0	NEAR BAY
4	-122.25	37.85	52.0	1627.0	280.0	565.0	259.0	3.8462	342200.0	NEAR BAY
...	...	...	...	...	...	...	...	...	...	...
20635	-121.09	39.48	25.0	1665.0	374.0	845.0	330.0	1.5603	78100.0	INLAND
20636	-121.21	39.49	18.0	697.0	150.0	356.0	114.0	2.5568	77100.0	INLAND
20637	-121.22	39.43	17.0	2254.0	485.0	1007.0	433.0	1.7000	92300.0	INLAND
20638	-121.32	39.43	18.0	1860.0	409.0	741.0	349.0	1.8672	84700.0	INLAND
20639	-121.24	39.37	16.0	2785.0	616.0	1387.0	530.0	2.3886	89400.0	INLAND

20640 rows × 10 columns

10개 특성의 이름은 다음과 같다.

housing.columns

Index(['longitude', 'latitude', 'housing_median_age', 'total_rooms',
       'total_bedrooms', 'population', 'households', 'median_income',
       'median_house_value', 'ocean_proximity'],
      dtype='object')

info() 메서드를 이용하여 데이터셋 전체에 대한 기본 정보를 확인한다.

'total_bedrooms' 특성: 207개의 결측치 포함
'ocean_proximity' 특성: 수치형 데이터 아님

housing.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 10 columns):
 #   Column              Non-Null Count  Dtype  
---  ------              --------------  -----  
 0   longitude           20640 non-null  float64
 1   latitude            20640 non-null  float64
 2   housing_median_age  20640 non-null  float64
 3   total_rooms         20640 non-null  float64
 4   total_bedrooms      20433 non-null  float64
 5   population          20640 non-null  float64
 6   households          20640 non-null  float64
 7   median_income       20640 non-null  float64
 8   median_house_value  20640 non-null  float64
 9   ocean_proximity     20640 non-null  object 
dtypes: float64(9), object(1)
memory usage: 1.6+ MB

'ocean_proximity' 특성은 구역별로 5개의 범주로 구분된 해안 근접도를 나타낸다.

해안근접도	의미
Near Bay	샌프란시스코의 Bay Area 근처 구역
<1H OCEAN	바다로부터 1시간 이내 거리
INLAND	내륙
NEAR OCEAN	해안가
ISLAND	섬

housing["ocean_proximity"].unique()

array(['NEAR BAY', '<1H OCEAN', 'INLAND', 'NEAR OCEAN', 'ISLAND'],
      dtype=object)

해안 근접도별 구역 수는 다음과 같다.

housing["ocean_proximity"].value_counts()

<1H OCEAN     9136
INLAND        6551
NEAR OCEAN    2658
NEAR BAY      2290
ISLAND           5
Name: ocean_proximity, dtype: int64

30.2. 데이터 특성 살펴보기#

30.2.1. 위치 정보 시각화#

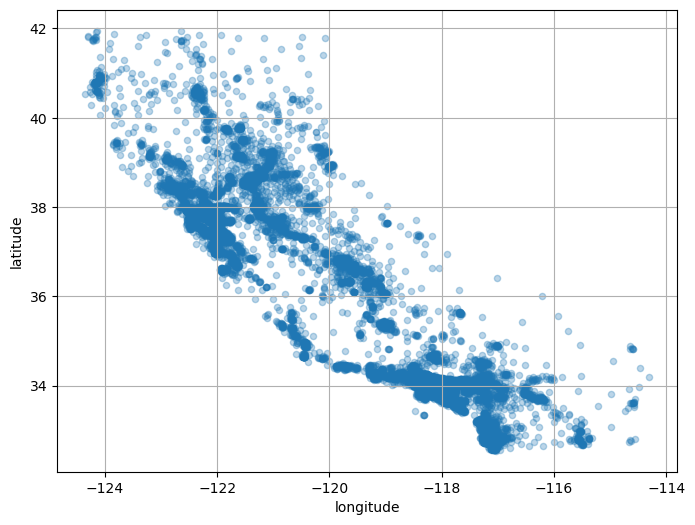
경도와 위도 정보를 이용해서 구역의 분포를 살펴본다.

housing.plot(kind="scatter", x="longitude", y="latitude", grid=True, alpha=0.3, figsize=(8, 6))
plt.show()

_images/8c9690f0d3afdadd6a8b52a32c2c1ad6767a8d6ea3ae6c21ff33ea785def5d0b.png

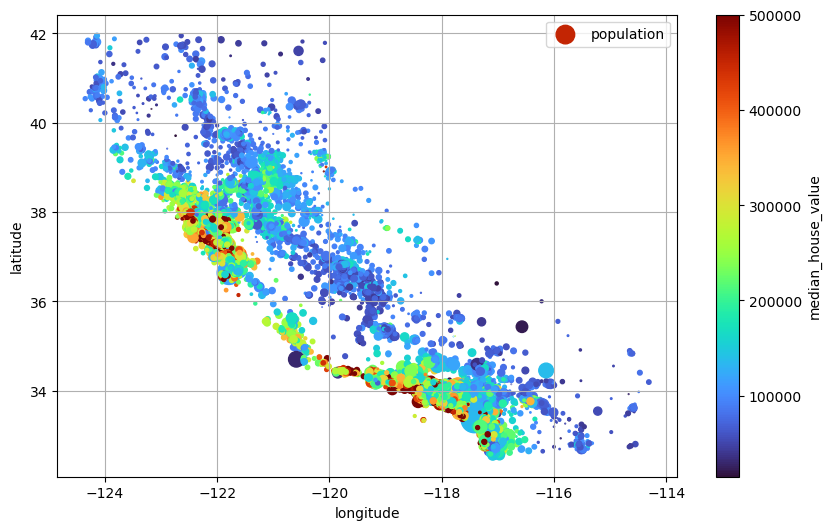
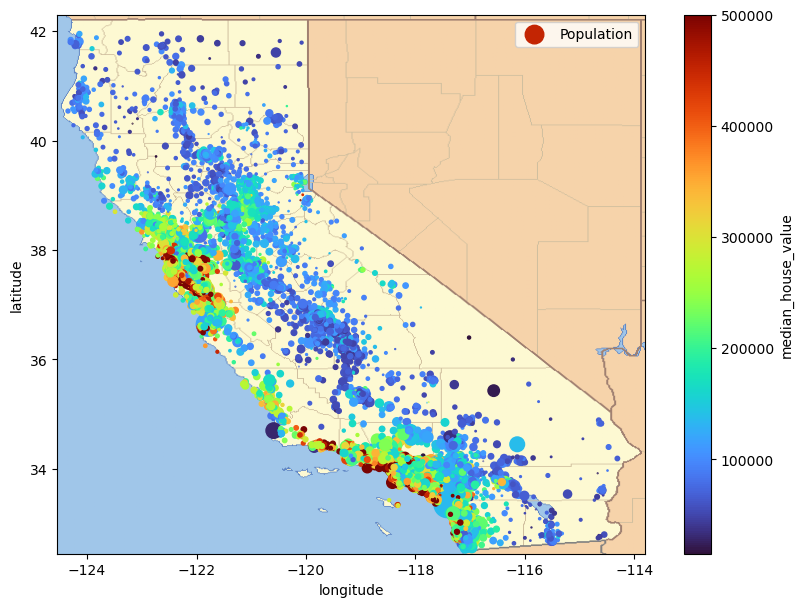
주택 중위가격을 색상으로 활용하면 다른 정보를 준다.

s=housing["population"] / 100: 구역별 인구수에 비례해서 원의 크기 지정
c="median_house_value": 주택 중위가격을 색상 지정에 이용
cmap="turbo": colormap 지정

housing.plot(kind="scatter", 
             x="longitude", 
             y="latitude", 
             grid=True,
             s=housing["population"] / 100, label="population",
             c="median_house_value", 
             cmap="turbo", 
             colorbar=True,
             figsize=(10, 6))
plt.show()

_images/de7782da4dfe47eb501bb4621f77e4fb09cc87acd4e1ff31f5494b72d976ea1e.png

캘리포니아 실제 지도위에 그래프를 그린다.

# 캘리포니아 지도 다운로드

IMAGES_PATH = Path() / "images"  # 이미지 저장 경로
filename = "california.png"      # 이미지 파일명
if not (IMAGES_PATH / filename).is_file():  # 이미지 파일이 없으면 다운로드 후 저장
    homl3_root = "https://github.com/ageron/handson-ml3/raw/main/"
    url = homl3_root + "images/end_to_end_project/" + filename
    print("Downloading", filename)
    urllib.request.urlretrieve(url, IMAGES_PATH / filename)

# 위도/경도를 이용한 구역별 인구 산포도
housing.plot(kind="scatter", 
                     x="longitude", 
                     y="latitude",
                     s=housing["population"] / 100, label="Population",
                     c="median_house_value", 
                     cmap="turbo", 
                     colorbar=True,
                     figsize=(10, 7))

# 다운로드된 캘리포티아 지도 표시
california_img = plt.imread(IMAGES_PATH / filename)
axis = -124.55, -113.8, 32.45, 42.3                # x축, y축 눈금
plt.axis(axis)
plt.imshow(california_img, extent=axis)

plt.show()

_images/b030662dbfe62b148c6600862e7baeed2fa1138a20229367c19d51758210cfb1.png

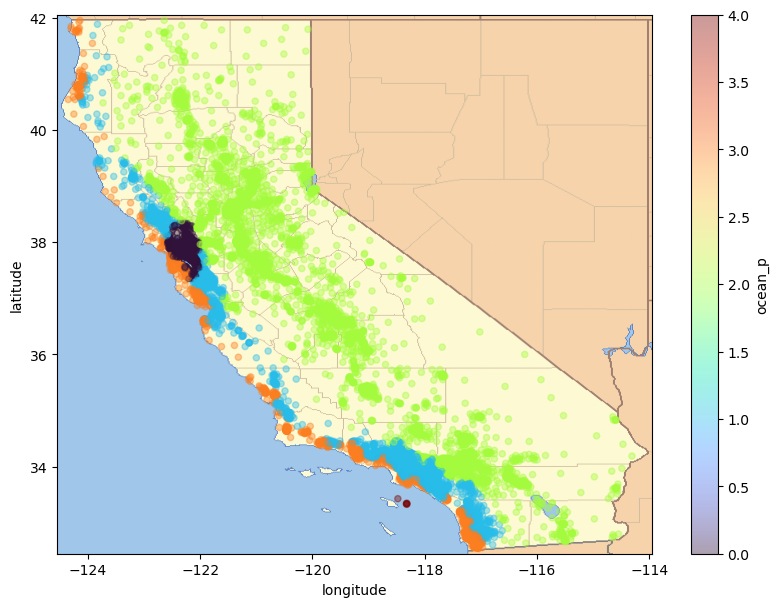
30.2.2. 해안 근접도 시각화#

해안 근접도에 따른 구역의 위치를 지도에 확인한다. 이를 위해 해안 근접도 특성을 정수화 한다. 이유는 데이터프레임의 항목별로 색깔을 지정하려면 숫자로 값을 변환해야 하기 때문이다.

해안 근접도	숫자
Near Bay	0
<1H Ocean	1
INLAND	2
Near Ocean	3
ISLAND	4

pd.factorize() 함수는 범주형 데이터를 수치형 데이터로 변환한다. 반환값은 변환된 숫자로 구성된 넘파이 어레이와 변환에 사용된 순서대로의 범주형 데이터로 구성된 인덱스로 구성된 튜플이다.

pd.factorize(housing["ocean_proximity"])

(array([0, 0, 0, ..., 2, 2, 2], dtype=int64),
 Index(['NEAR BAY', '<1H OCEAN', 'INLAND', 'NEAR OCEAN', 'ISLAND'], dtype='object'))

해안 근접도가 수치형 데이터로 변환된 값으로 구성된 'ocean_p' 특성을 추가한다. 이를 위해 앞서 설명한 대로 pd.factorize() 함수의 반환값의 첫째 항목을 이용한다.

housing["ocean_p"] = pd.factorize(housing["ocean_proximity"])[0]

이제 해안 근접도를 색상으로 지정하고 산점도를 캘리포니아 지도와 함께 그리면 해안 근접도의 의미가 보다 분명해진다.

# 위도/경도를 이용한 구역별 인구 산포도
housing.plot(kind="scatter", 
                     x="longitude", 
                     y="latitude",
                     c="ocean_p", 
                     cmap="turbo", 
                     colorbar=True,
                     alpha=0.4,        # 투명도 조절
                     figsize=(10, 7))

# 다운로드된 캘리포티아 지도
california_img = plt.imread(IMAGES_PATH / filename)
axis = -124.55, -113.95, 32.45, 42.05  # x축, y축 눈금
plt.axis(axis)
plt.imshow(california_img, extent=axis)

plt.show()

_images/17d8687a334d67af9652f588a21511be3934d3b098d33e6939b0c78c70e879aa.png

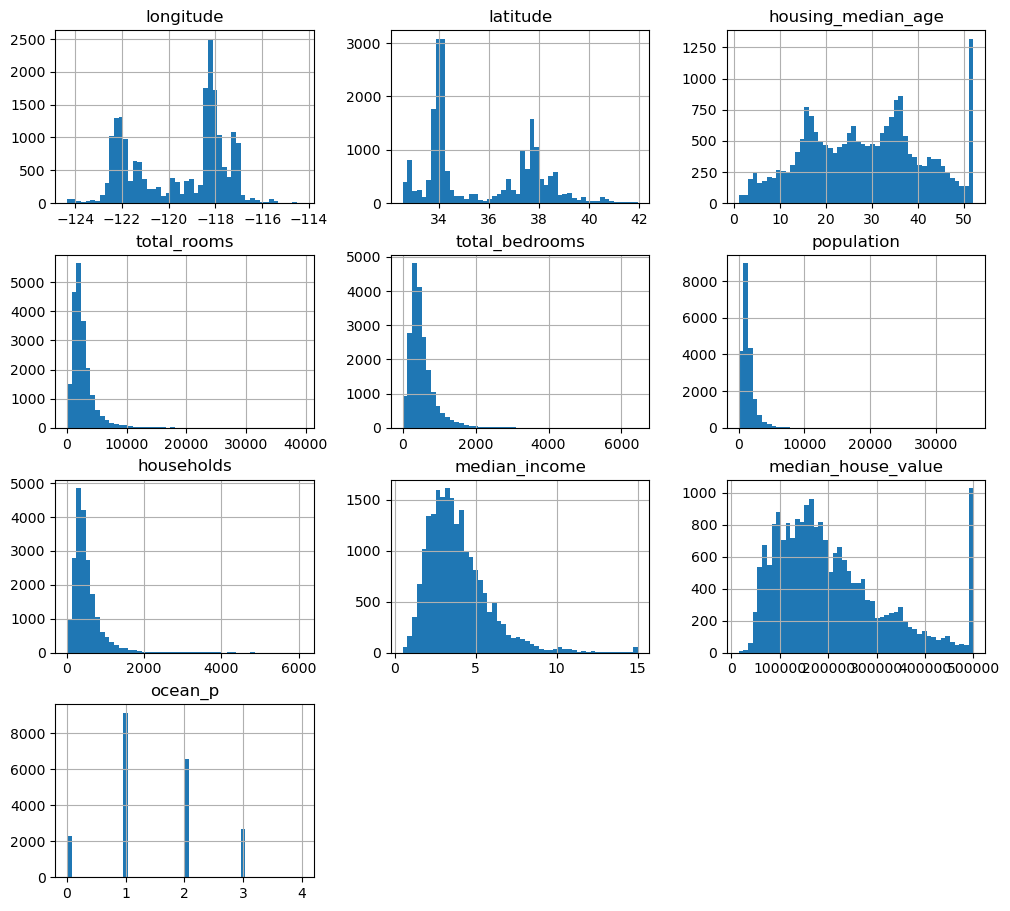
30.2.3. 특성별 히스토그램#

hist() 메서드는 수치형 특성(라벨)에 대해 히스토그램을 그린다. 여기서는 해안 근접도를 수치화한 특성을 포함해서 10개의 특성에 대한 히스토그램을 그린다. 해안 근접도 히스토그램을 통해 1번, 즉 해안으로부터 1시간 이내에 위치한 구역이 가장 많음을 알 수 있다.

housing.hist(bins=50, figsize=(12, 11))
plt.show()

_images/8047372e4762c5b2173f313f11b3512ae762bf582c3f72b0db2dbeb169311e70.png

30.2.4. 중위소득 구간 나누기#

'median_income' 특성의 히스토그램은 다음과 같다.

중위소득을 구간의 크기를 1.5 정도로 총 5개 구간으로 쪼개 후 각 구간에 대해 1, 2, 3, 4, 5의 라벨을 사용한다.

구간	라벨
1.5 이하	1
(1.5, 3.0]	2
(3.0. 4.5]	3
(4.5, 6.0]	4
6.0 초과	5

bins=[0., 1.5, 3.0, 4.5, 6., np.inf]

housing_income_cat = pd.cut(housing["median_income"],
                            bins=bins,
                            labels=[1, 2, 3, 4, 5])

housing_income_cat

      5
      5
      5
      4
      3
        ..
  2
  2
  2
  2
  2
Name: median_income, Length: 20640, dtype: category
Categories (5, int64): [1 < 2 < 3 < 4 < 5]

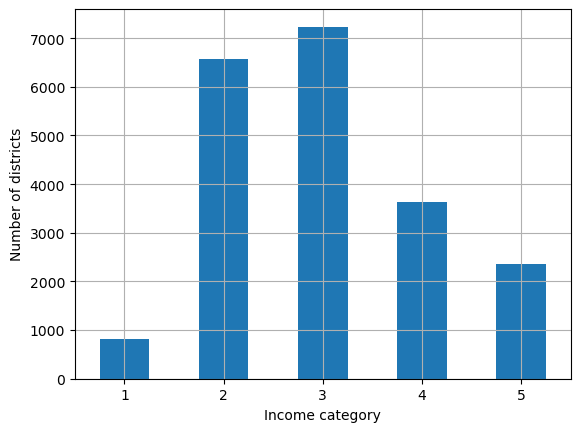
중위소득 구간별 구역의 수를 확인하고 인덱스를 기준으로 정렬한다.

housing_income_cat_sorted_index = housing_income_cat.value_counts().sort_index()
housing_income_cat_sorted_index

   822
  6581
  7236
  3639
  2362
Name: median_income, dtype: int64

중위소득 구간별 구역의 수를 막대그래프로 그린다.

housing_income_cat_sorted_index.plot(kind='bar', rot=0, grid=True)
plt.xlabel("Income category")
plt.ylabel("Number of districts")
plt.show()

_images/a26465bfe4bc1e26f46c86d5c21d19b5736fa400b764baaa3bcd15415791b143.png

30.2.5. 특성별 상관관계#

수치형 특성들 사이의 상관관계를 계산한다.

corr_matrix = housing.corr(numeric_only=True)
corr_matrix

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value	ocean_p
longitude	1.000000	-0.924664	-0.108197	0.044568	0.069608	0.099773	0.055310	-0.015176	-0.045967	0.180381
latitude	-0.924664	1.000000	0.011173	-0.036100	-0.066983	-0.108785	-0.071035	-0.079809	-0.144160	-0.067586
housing_median_age	-0.108197	0.011173	1.000000	-0.361262	-0.320451	-0.296244	-0.302916	-0.119034	0.105623	-0.204882
total_rooms	0.044568	-0.036100	-0.361262	1.000000	0.930380	0.857126	0.918484	0.198050	0.134153	0.014818
total_bedrooms	0.069608	-0.066983	-0.320451	0.930380	1.000000	0.877747	0.979728	-0.007723	0.049686	0.004081
population	0.099773	-0.108785	-0.296244	0.857126	0.877747	1.000000	0.907222	0.004834	-0.024650	-0.008511
households	0.055310	-0.071035	-0.302916	0.918484	0.979728	0.907222	1.000000	0.013033	0.065843	-0.016911
median_income	-0.015176	-0.079809	-0.119034	0.198050	-0.007723	0.004834	0.013033	1.000000	0.688075	-0.129135
median_house_value	-0.045967	-0.144160	0.105623	0.134153	0.049686	-0.024650	0.065843	0.688075	1.000000	-0.210600
ocean_p	0.180381	-0.067586	-0.204882	0.014818	0.004081	-0.008511	-0.016911	-0.129135	-0.210600	1.000000

주택 중위가격과 기타 특성들 사이의 상관관계는 다음과 같다. 또한 상관관계가 높은 순서대로 정렬한다.

corr_matrix["median_house_value"].sort_values(ascending=False)

median_house_value    1.000000
median_income         0.688075
total_rooms           0.134153
housing_median_age    0.105623
households            0.065843
total_bedrooms        0.049686
population           -0.024650
longitude            -0.045967
latitude             -0.144160
ocean_p              -0.210600
Name: median_house_value, dtype: float64

주택 중위가격과 중위소득 사이의 상관관계가 가장 높다. 반면에 건축물 중위연령은 주택 중위가격이나 중위소득과 별 상관이 없어 보인다. 이런 사실을 세 특성들 사이의 일대일 산점도를 그려 확인할 수 있다. 여러 특성들 사이의 일대일 산점도를 함 전에 그리는 pd.plotting.scatter_matrix() 함수를 이용한다. 자신과의 상관관계는 전혀 중요하지 않기에 대각선상은 각 특성의 히스토그램이 그려진다.

from pandas.plotting import scatter_matrix

attributes = ["median_house_value", "median_income", "housing_median_age"]
scatter_matrix(housing[attributes], figsize=(10, 6))
plt.show()

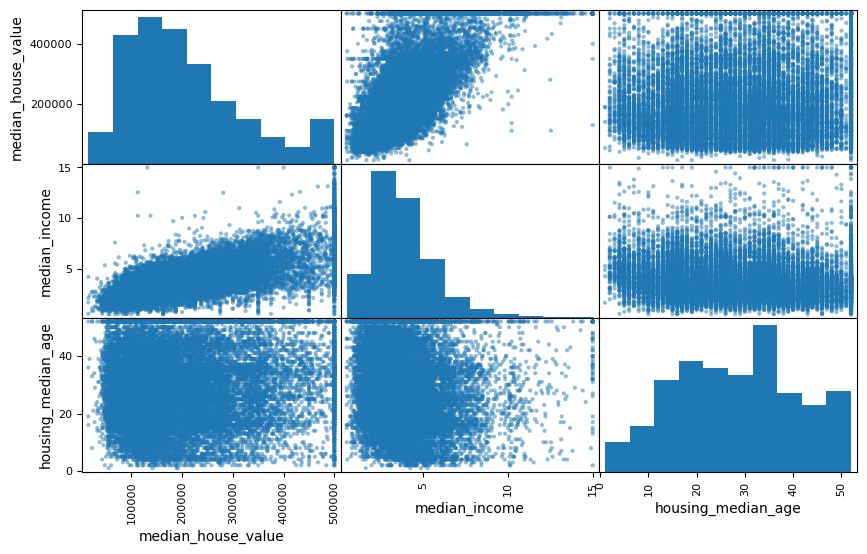
_images/1b99f986ae7d36a36c0eb1d02fbb32a541775e0372a8d80c6e6a377a8b18c68c.png

30.3. 데이터 전처리#

30.3.1. 이상치 처리#

중위소득과 주택 중위가격 사이의 상관관계만 따로 확대해서 보면 다음과 같다.

housing.plot(kind="scatter", 
             x="median_income", 
             y="median_house_value",
             alpha=0.5, 
             grid=True)
plt.show()

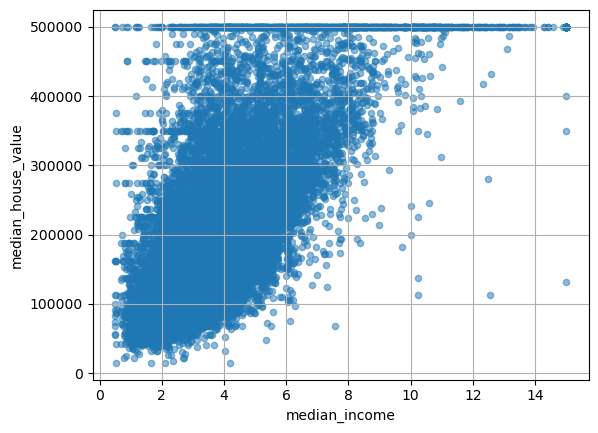
_images/702a9b8232b9ca7f19cc97e200aa1b49d56b6406908f170bb906f848b5d791be.png

주택 중위가격이 50만 달러에 해당하는 데이터가 좀 이상하다. 그림에서 보여지듯이 칼로 자른 듯한 데이터는 현실에서는 존재하지 않는다. 아마도 50만 달러 이상은 모두 50만 달러로 자른 것 같다.

이런 경우엔 해당 데이터들을 이상치로 간주해서 삭제하는 게 좋다. value_counts() 메서드를 이용하여 확인하면 정확히 50만1달러 샘플이 965개 있다 따라서, 50만 달러를 초과하는 주택은 50만1달러로 통일한 것으로 보인다.

housing.median_house_value.value_counts()

500001.0    965
137500.0    122
162500.0    117
112500.0    103
187500.0     93
           ... 
41000.0       1
328200.0      1
300500.0      1
487500.0      1
47000.0       1
Name: median_house_value, Length: 3842, dtype: int64

주택 중위소득이 50만1달러인 샘플은 제외한다.

mask = housing.median_house_value != 500001
housing = housing[mask].copy()

50만1달러 주택은 모두 제외시켰다. 이제 가장 비싼 주택 중위가격은 50만 달러다.

housing.median_house_value.describe()

count     19675.000000
mean     192477.921017
std       97711.509613
min       14999.000000
25%      116600.000000
50%      173800.000000
75%      248200.000000
max      500000.000000
Name: median_house_value, dtype: float64

산점도를 다시 그리면 이상한 선이 더 이상 보이지 않는다.

housing.plot(kind="scatter", 
             x="median_income", 
             y="median_house_value",
             alpha=0.5, 
             grid=True)
plt.show()

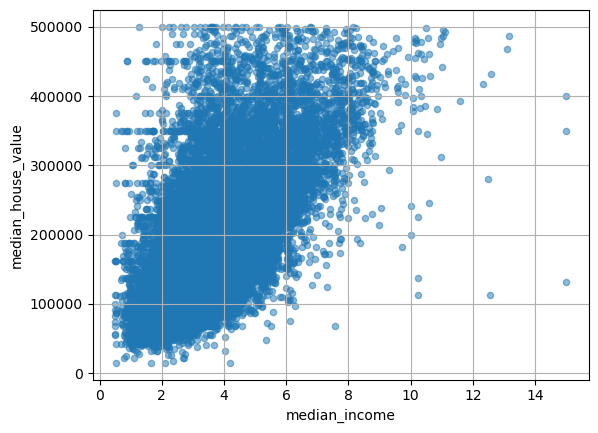
_images/05873834a9e0799d48916bc026ca9a0b8381ebcca624cca53b87f9a0a8a972f5.png

30.3.2. 결측치 처리#

total_bedrooms 특성(라벨)에 결측치가 200개 있다. 원래 207개 이지만 앞서 50만1달러 주택 중위가격 데이터를 삭제했기 때문에 200개로 줄었다.

housing.isnull().sum()

longitude               0
latitude                0
housing_median_age      0
total_rooms             0
total_bedrooms        200
population              0
households              0
median_income           0
median_house_value      0
ocean_proximity         0
ocean_p                 0
dtype: int64

결측치를 포함한 데이터 샘플을 다음과 같이 확인한다.

mask = housing.isnull().any(axis=1)
housing[mask]

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value	ocean_proximity	ocean_p
182	-118.27	34.04	13.0	1784.0	NaN	2158.0	682.0	1.7038	118100.0	<1H OCEAN	1
327	-117.65	34.04	15.0	3393.0	NaN	2039.0	611.0	3.9336	151000.0	INLAND	2
366	-122.50	37.75	44.0	1819.0	NaN	1137.0	354.0	3.4919	271800.0	NEAR OCEAN	3
477	-117.99	34.14	30.0	2346.0	NaN	1988.0	474.0	2.5625	153000.0	INLAND	2
495	-114.59	34.83	41.0	812.0	NaN	375.0	158.0	1.7083	48500.0	INLAND	2
...	...	...	...	...	...	...	...	...	...	...	...
19880	-118.23	33.94	36.0	1110.0	NaN	1417.0	302.0	2.3333	92100.0	<1H OCEAN	1
19952	-119.19	34.20	18.0	3620.0	NaN	3171.0	779.0	3.3409	220500.0	NEAR OCEAN	3
20088	-119.73	36.83	8.0	3602.0	NaN	1959.0	580.0	5.3478	138800.0	INLAND	2
20325	-118.88	34.17	15.0	4260.0	NaN	1701.0	669.0	5.1033	410700.0	<1H OCEAN	1
20345	-122.22	38.15	7.0	5129.0	NaN	2824.0	738.0	5.5138	171100.0	NEAR BAY	0

200 rows × 11 columns

데이터 샘플 수는 200개로 다시 한 번 확인된다.

housing[mask].shape

(200, 11)

결측치를 포함한 데이터 샘플은 삭제하거나 아니면 다른 값으로 채운다. 여기서는 해당 열의 중위수로 채우는 방식을 이용한다. 아래 코드는 'total_bedrooms' 열의 중위수로 결측치를 채운다.

median = housing["total_bedrooms"].median()
housing["total_bedrooms"].fillna(median, inplace=True)

결측치가 모두 중위수로 변환된 것을 확인할 수 있다.

housing[mask]

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value	ocean_proximity	ocean_p
182	-118.27	34.04	13.0	1784.0	436.0	2158.0	682.0	1.7038	118100.0	<1H OCEAN	1
327	-117.65	34.04	15.0	3393.0	436.0	2039.0	611.0	3.9336	151000.0	INLAND	2
366	-122.50	37.75	44.0	1819.0	436.0	1137.0	354.0	3.4919	271800.0	NEAR OCEAN	3
477	-117.99	34.14	30.0	2346.0	436.0	1988.0	474.0	2.5625	153000.0	INLAND	2
495	-114.59	34.83	41.0	812.0	436.0	375.0	158.0	1.7083	48500.0	INLAND	2
...	...	...	...	...	...	...	...	...	...	...	...
19880	-118.23	33.94	36.0	1110.0	436.0	1417.0	302.0	2.3333	92100.0	<1H OCEAN	1
19952	-119.19	34.20	18.0	3620.0	436.0	3171.0	779.0	3.3409	220500.0	NEAR OCEAN	3
20088	-119.73	36.83	8.0	3602.0	436.0	1959.0	580.0	5.3478	138800.0	INLAND	2
20325	-118.88	34.17	15.0	4260.0	436.0	1701.0	669.0	5.1033	410700.0	<1H OCEAN	1
20345	-122.22	38.15	7.0	5129.0	436.0	2824.0	738.0	5.5138	171100.0	NEAR BAY	0

200 rows × 11 columns

이제 데이터셋에 결측치가 하나도 없다.

housing.isnull().sum()

longitude             0
latitude              0
housing_median_age    0
total_rooms           0
total_bedrooms        0
population            0
households            0
median_income         0
median_house_value    0
ocean_proximity       0
ocean_p               0
dtype: int64

30.3.3. 데이터 스케일링#

데이터 스케일링은 수치형 특성에 포함된 데이터의 크기(scale)를 조정하는 기법을 가리킨다. 데이터분석 분야에서 가장 많이 활용되는 스케일링 기법은 다음 세가지다.

표준화
정규화
로그 변환

30.3.3.1. 표준화#

표준화는 특성(열)별로 평균값은 0, 표준편차는 1이 되도록 값들을 변환시키는 기법이다. 즉, 아래 식에서 처럼 원래의 값 \(x\)에서 해당 데이터셋의 평균값(\(\mu\))을 뺀 다음에 해당 데이터셋의 표준편차(\(\sigma\))로 나눈다.

\[z = \frac{x - \mu}{\sigma}\]

변환된 값 \(z\)로 구성된 데이터셋의 평균값은 0, 표준편차는 1이 되어 표준정규분포에 가까운 데이터 분포를 갖는다. 각 특성의 평균값과 표준편차를 먼저 계산하기 위해 해안 근접도 특성을 제외한 모든 특성이 수치형 특성이기에 제외한다.

housing_numerical = housing.drop(["ocean_proximity", "ocean_p"], axis=1)
housing_numerical

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value
0	-122.23	37.88	41.0	880.0	129.0	322.0	126.0	8.3252	452600.0
1	-122.22	37.86	21.0	7099.0	1106.0	2401.0	1138.0	8.3014	358500.0
2	-122.24	37.85	52.0	1467.0	190.0	496.0	177.0	7.2574	352100.0
3	-122.25	37.85	52.0	1274.0	235.0	558.0	219.0	5.6431	341300.0
4	-122.25	37.85	52.0	1627.0	280.0	565.0	259.0	3.8462	342200.0
...	...	...	...	...	...	...	...	...	...
20635	-121.09	39.48	25.0	1665.0	374.0	845.0	330.0	1.5603	78100.0
20636	-121.21	39.49	18.0	697.0	150.0	356.0	114.0	2.5568	77100.0
20637	-121.22	39.43	17.0	2254.0	485.0	1007.0	433.0	1.7000	92300.0
20638	-121.32	39.43	18.0	1860.0	409.0	741.0	349.0	1.8672	84700.0
20639	-121.24	39.37	16.0	2785.0	616.0	1387.0	530.0	2.3886	89400.0

19675 rows × 9 columns

특성별 평균값

mean_df = housing_numerical.mean()
mean_df

longitude               -119.563192
latitude                  35.651780
housing_median_age        28.386277
total_rooms             2619.763659
total_bedrooms           538.592173
population              1440.812198
households               501.186023
median_income              3.676717
median_house_value    192477.921017
dtype: float64

특성별 표준편차

std_df = housing_numerical.std()
std_df

longitude                 2.006108
latitude                  2.149802
housing_median_age       12.509113
total_rooms            2181.348207
total_bedrooms          420.389237
population             1143.648725
households              383.264636
median_income             1.570272
median_house_value    97711.509613
dtype: float64

수치형 특성의 표준화는 이제 매우 간단하게 계산된다.

housing_standardized = housing_numerical.sub(mean_df, axis=1).div(std_df, axis=1)
housing_standardized

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value
0	-1.329344	1.036477	1.008363	-0.797563	-0.974317	-0.978283	-0.978922	2.960305	2.662144
1	-1.324359	1.027174	-0.590472	2.053426	1.349720	0.839583	1.661552	2.945148	1.699105
2	-1.334329	1.022522	1.887722	-0.528464	-0.829213	-0.826138	-0.845854	2.280295	1.633606
3	-1.339313	1.022522	1.887722	-0.616941	-0.722169	-0.771926	-0.736269	1.252257	1.523076
4	-1.339313	1.022522	1.887722	-0.455115	-0.615126	-0.765805	-0.631903	0.107932	1.532287
...	...	...	...	...	...	...	...	...	...
20635	-0.761079	1.780732	-0.270705	-0.437694	-0.391523	-0.520975	-0.446652	-1.347803	-1.170568
20636	-0.820897	1.785383	-0.830297	-0.881457	-0.924363	-0.948554	-1.010232	-0.713200	-1.180802
20637	-0.825881	1.757474	-0.910239	-0.167678	-0.127482	-0.379323	-0.177908	-1.258838	-1.025242
20638	-0.875729	1.757474	-0.830297	-0.348300	-0.308267	-0.611912	-0.397078	-1.152359	-1.103022
20639	-0.835851	1.729564	-0.990180	0.075750	0.184134	-0.047053	0.075180	-0.820315	-1.054921

19675 rows × 9 columns

변환된 데이터들의 분포를 확인하면 실제로 특성별로 평균값은 거의 0, 표준편차는 거의 1로 확인된다.

housing_standardized.describe().loc[["mean", "std"]]

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value
mean	-1.261100e-15	-2.065720e-16	-9.154896e-17	7.493653e-17	1.305521e-16	-1.950155e-17	2.907176e-17	2.329352e-17	-9.823005e-17
std	1.000000e+00	1.000000e+00	1.000000e+00	1.000000e+00	1.000000e+00	1.000000e+00	1.000000e+00	1.000000e+00	1.000000e+00

30.3.3.2. 정규화#

정규화는 특성별로 최소값은 0, 최대값은 1로 만들며 아래 공식을 이용한다.

\[z = \frac{x-\min}{\max-\min}\]

\(\max\)와 \(\min\)은 각각 특성별 최대값과 최소값을 가리킨다. 그러면 \(x=\min\)일 때 \(z=0\)이 되고, \(x=\max\)일 때 \(z=1\)이 된다.

특성별 최대값

max_df = housing_numerical.max()
max_df

longitude               -114.3100
latitude                  41.9500
housing_median_age        52.0000
total_rooms            39320.0000
total_bedrooms          6445.0000
population             35682.0000
households              6082.0000
median_income             15.0001
median_house_value    500000.0000
dtype: float64

특성별 최소값

min_df = housing_numerical.min()
min_df

longitude              -124.3500
latitude                 32.5400
housing_median_age        1.0000
total_rooms               2.0000
total_bedrooms            2.0000
population                3.0000
households                2.0000
median_income             0.4999
median_house_value    14999.0000
dtype: float64

수치형 특성의 정규화는 다음과 같다.

housing_normalized = housing_numerical.sub(min_df, axis=1).div(max_df - min_df, axis=1)
housing_normalized

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value
0	0.211155	0.567481	0.784314	0.022331	0.019711	0.008941	0.020395	0.539668	0.902268
1	0.212151	0.565356	0.392157	0.180503	0.171349	0.067210	0.186842	0.538027	0.708248
2	0.210159	0.564293	1.000000	0.037260	0.029179	0.013818	0.028783	0.466028	0.695052
3	0.209163	0.564293	1.000000	0.032352	0.036163	0.015555	0.035691	0.354699	0.672784
4	0.209163	0.564293	1.000000	0.041330	0.043148	0.015752	0.042270	0.230776	0.674640
...	...	...	...	...	...	...	...	...	...
20635	0.324701	0.737513	0.470588	0.042296	0.057737	0.023599	0.053947	0.073130	0.130105
20636	0.312749	0.738576	0.333333	0.017676	0.022971	0.009894	0.018421	0.141853	0.128043
20637	0.311753	0.732200	0.313725	0.057277	0.074965	0.028140	0.070888	0.082764	0.159383
20638	0.301793	0.732200	0.333333	0.047256	0.063169	0.020684	0.057072	0.094295	0.143713
20639	0.309761	0.725824	0.294118	0.070782	0.095297	0.038790	0.086842	0.130253	0.153404

19675 rows × 9 columns

실제로 특성별 최소값은 0, 최대값은 1이다.

housing_normalized.describe().loc[["min", "max"]]

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value
min	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
max	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0

30.3.3.3. 로그 변환#

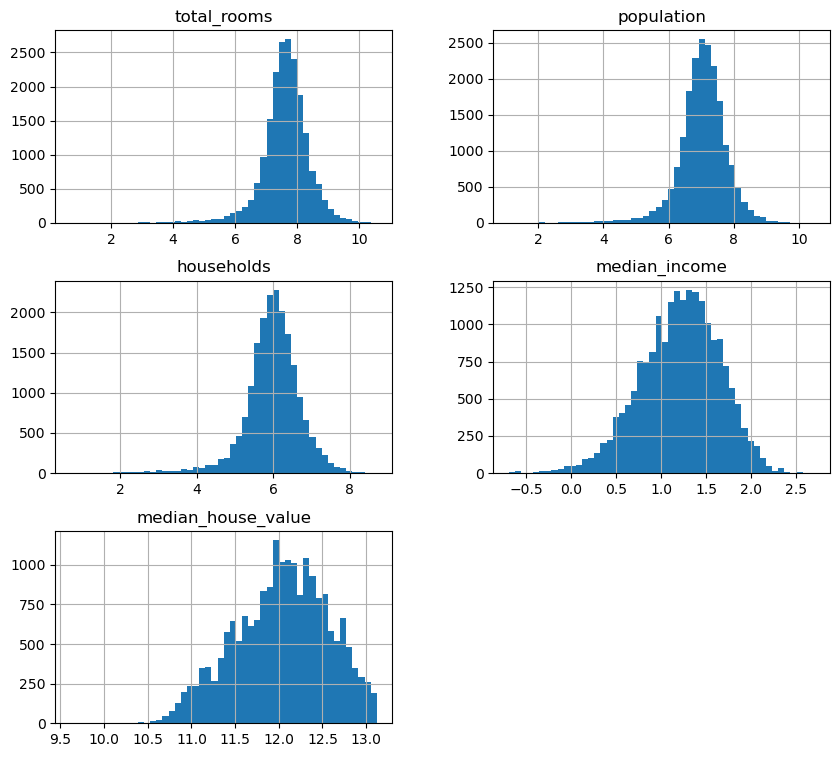
다음 다섯 개 특성의 히스토그램을 보면 데이터의 분포가 정규분포를 따르지 않는다.

housing_numerical[["total_rooms", "population","households", "median_income", "median_house_value"]].hist(bins=50, figsize=(10, 9))
plt.show()

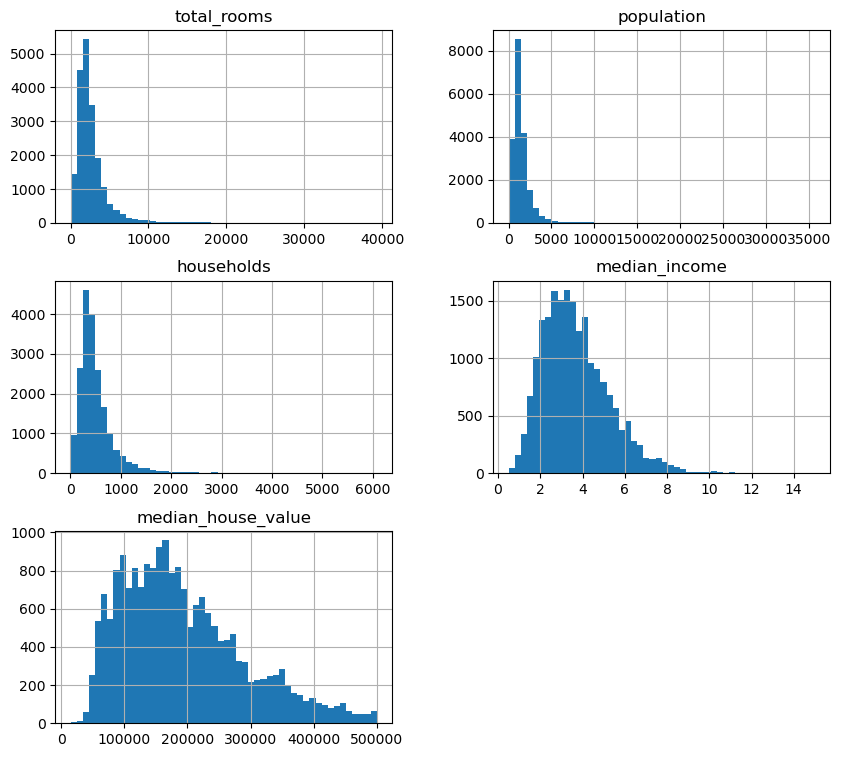
_images/deccf7ac9f8966f7766517cb5f8501a891c00f6ed73b06028fbd41f580055e4b.png

이런 경우 모든 값들에 대해 로그 함수를 적용하여 변환하면 보다 정규분포에 가까운 히스토그램을 얻는다. 이렇게 모든 값에 np.log() 함수를 적용해서 데이터를 변환하는 기법이 로그 변환이다.

housing_log_transfomred = housing_numerical[["total_rooms", "population","households", "median_income", "median_house_value"]].apply(np.log)
housing_log_transfomred

	total_rooms	population	households	median_income	median_house_value
0	6.779922	5.774552	4.836282	2.119287	13.022764
1	8.867709	7.783641	7.037028	2.116424	12.789684
2	7.290975	6.206576	5.176150	1.982022	12.771671
3	7.149917	6.324359	5.389072	1.730434	12.740517
4	7.394493	6.336826	5.556828	1.347086	12.743151
...	...	...	...	...	...
20635	7.417580	6.739337	5.799093	0.444878	11.265745
20636	6.546785	5.874931	4.736198	0.938756	11.252859
20637	7.720462	6.914731	6.070738	0.530628	11.432799
20638	7.528332	6.608001	5.855072	0.624440	11.346871
20639	7.932003	7.234898	6.272877	0.870707	11.400876

19675 rows × 5 columns

변환된 특성들의 히스토그램을 보면 보다 정규분포에 가까워졌다.

housing_log_transfomred.hist(bins=50, figsize=(10, 9))
plt.show()

_images/ac6d534f03dc6bdf622a5bf4d41490a1c7def0a36f169f5166156d994fe14f42.png

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value
min	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
max	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value
min	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
max	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0

캘리포니아 주택 가격

Contents

30. 캘리포니아 주택 가격#

30.1. 캘리포니아 데이터셋#

30.1.1. 캘리포니아 데이터셋 다운로드#

30.1.2. 데이터셋 기본 정보 확인#

30.2. 데이터 특성 살펴보기#

30.2.1. 위치 정보 시각화#

30.2.2. 해안 근접도 시각화#

30.2.3. 특성별 히스토그램#

30.2.4. 중위소득 구간 나누기#

30.2.5. 특성별 상관관계#

30.3. 데이터 전처리#

30.3.1. 이상치 처리#

30.3.2. 결측치 처리#

30.3.3. 데이터 스케일링#

30.3.3.1. 표준화#

30.3.3.2. 정규화#

30.3.3.3. 로그 변환#

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	median_house_value
min	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
max	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0