10. 선형대수 기초#
참고
여기서 사용하는 코드는 조엘 그루스(Joel Grus)의 밑바닥부터 시작하는 데이터 과학 4장에 사용된 소스코드의 일부를 기반으로 작성되었다.
주요 내용
선형대수의 주요 개념인 벡터와 행렬을 각각 1차원과 2차원 리스트로 구현하여 실용적으로 사용하는 과정을 살펴본다.
특히 벡터와 행렬의 연산 등을 모두 리스트를 이용하여 구현한다.
이를 위해 조건제시법을 많이 활용한다.
앞으로 넘파이 어레이에서 배울 numpy.array 자료형이 제공하는 다양한 기능에 대한 보다 깊은 이해에
도움될 것으로 기대한다.
10.1. 벡터#
벡터는 유한 개의 값으로 구성된다. 보통 수를 항목으로 사용하며, 항목의 수를 벡터의 차원dimension이라 부른다. 벡터는 수학, 통계, 물리 등 과학 분야에서 많이 사용되며, 최근에 컴퓨터 데이터 분석이 발전하면서 벡터의 활용도 매우 높아졌다.
2차원 평면 공간에서 방향과 크기를 표현하는 2차원 벡터:
[x, y]
사람들의 키, 몸무게, 나이로 이루어진 3차원 벡터:
[키, 몸무게, 나이]
네 번의 시험 점수로 이루어진 4차원 벡터:
[1차점수, 2차점수, 3차점수, 4차점수]
10.1.1. 리스트와 벡터#
리스트를 이용하여 벡터를 구현할 수 있다.
x축, y축 좌표로 구성된 2차원 벡터
# [x좌표, y좌표]
twoDVector1 = [3, 1]
twoDVector2 = [-2, 5]
키, 몸무게, 나이로 구성된 3차원 벡터
# [키, 몸무게, 나이]
height_weight_age1 = [70, 170, 50]
height_weight_age2 = [66, 163, 50]
1차부터 4차까지의 시험 점수로 구성된 4차원 벡터
# [1차점수, 2차점수, 3차점수, 4차점수]
grades1 = [95, 80, 75, 62]
grades2 = [85, 82, 79, 82]
10.1.2. 벡터 항목별 연산#
벡터 항목별 덧셈
두 벡터의 항목별 덧셈은 같은 위치에 있는 항목끼기 더한 결과로 이루어진 벡터를 생성한다.
차원이 같은 두 벡터의 항목별 덧셈을 실행하는 함수는 다음과 같다.
def addV(u, v):
assert len(u) == len(v) # 두 벡터의 길이가 같은 경우만 취급
return [u_i + v_i for u_i, v_i in zip(u, v)]
addV(twoDVector1, twoDVector2)
[1, 6]
addV(height_weight_age1, height_weight_age2)
[136, 333, 100]
addV(grades1, grades2)
[180, 162, 154, 144]
벡터 리스트의 합
동일한 차원의 임의의 개수의 벡터를 항목별로 더하는 함수를 다음과 같이 정의할 수 있다.
함수의 본문에 사용된 all() 함수는 리스트, 튜플 등에 포함된 모든 항목이 참인 경우에만
참을 반환한다.
def vector_sum(vectors):
"""
vectors: 동일한 차원의 벡터들의 리스트
반환값: 각 항목의 합으로 이루어진 동일한 차원의 벡터
"""
# 입력값 확인
assert len(vectors) > 0 # 1개 이상의 벡터가 주어져야 함
num_elements = len(vectors[0]) # 벡터 개수
assert all(len(v) == num_elements for v in vectors) # 모든 벡터의 크기가 같아야 함
# 동일한 위치의 항목을 모두 더한 값들로 이루어진 벡터 반환
return [sum(vector[i] for vector in vectors) for i in range(num_elements)]
예를 들어, 2차원 벡터 네 개를 더한 결과는 다음과 같다.
vector_sum([[1, 2], [3, 4], [5, 6], [7, 8]])
[16, 20]
벡터 항목별 뺄셈
차원이 같은 벡터 두 개의 항목별 뺄셈은 같은 위치에 있는 항목끼기 뺀 결과로 이루어진 벡터를 생성한다.
차원이 같은 두 벡터의 항목별 뺄셈을 실행하는 함수는 다음과 같다.
def subtractV(v, w):
assert len(v) == len(w) # 두 벡터의 길이가 같은 경우만 취급
return [v_i - w_i for v_i, w_i in zip(v, w)]
subtractV(twoDVector1, twoDVector2)
[5, -4]
subtractV(height_weight_age1, height_weight_age2)
[4, 7, 0]
벡터 항목별 곱셈
차원이 같은 벡터 두 개의 항목별 곱셈은 같은 위치에 있는 항목끼기 곱한 결과로 이루어진 벡터를 생성한다.
차원이 같은 두 벡터의 항목별 곱셈을 실행하는 함수는 다음과 같다.
def multiplyV(v, w):
assert len(v) == len(w) # 두 벡터의 길이가 같은 경우만 취급
return [v_i * w_i for v_i, w_i in zip(v, w)]
multiplyV(twoDVector1, twoDVector2)
[-6, 5]
multiplyV(grades1, grades2)
[8075, 6560, 5925, 5084]
벡터 항목별 나눗셈
차원이 같은 벡터 두 개의 항목별 나눗셈은 같은 위치에 있는 항목끼기 나눈 결과로 이루어진 벡터를 생성한다.
차원이 같은 두 벡터의 항목별 나눗셈을 실행하는 함수는 다음과 같다.
def divideV(v, w):
assert len(v) == len(w) # 두 벡터의 길이가 같은 경우만 취급
return [v_i / w_i for v_i, w_i in zip(v, w)]
divideV(twoDVector1, twoDVector2)
[-1.5, 0.2]
divideV(grades1, grades2)
[1.1176470588235294, 0.975609756097561, 0.9493670886075949, 0.7560975609756098]
벡터 스칼라 곱셈
하나의 수와 하나의 벡터의 곱셈을 스칼라 곱셈이라 부른다. 스칼라 곱셈은 벡터의 각 항목을 지정된 수로 곱한다.
벡터의 각 항목에 동일한 부동소수점을 곱한 결과를 반환하는 함수는 다음과 같다.
def scalar_multiplyV(c, v):
return [c * v_i for v_i in v]
scalar_multiplyV(2, [1, 2, 3])
[2, 4, 6]
항목별 평균 벡터
여러 개의 동일 차원 벡터가 주어졌을 때 항목별 평균을 구할 수 있다. 항목별 평균은 항목끼리 모두 더한 후 벡터의 개수로 나눈다.
Example 10.1
3개의 2차원 벡터들의 평균은 아래와 같이 작동한다.
항목별 평균으로 이루어진 벡터를 반환하는 함수는 다음과 같이 벡터들의 합을 벡터의 개수로 나눈다.
def meanV(vectors):
n = len(vectors)
return scalar_multiplyV(1/n, vector_sum(vectors))
meanV([[3, 2], [2, 5], [7, 5], [6, 3]])
[4.5, 3.75]
meanV([[3, 2, 6], [2, 5, 9], [7, 5, 1], [6, 3, 4]])
[4.5, 3.75, 5.0]
10.1.3. 벡터 내적과 크기#
차원이 같은 벡터 두 개의 내적은 같은 위치에 있는 항목끼기 곱한 후 모두 더한 값이다. 벡터의 내적은 점곱dot product를 사용하며 벡터들의 곱과 구별된다.
벡터 내적 함수
동일 차원의 두 벡터의 내적을 반환하는 함수는 다음과 같다.
def dotV(v, w):
assert len(v) == len(w), "벡터들의 길이가 동일해야 함"""
return sum(v_i * w_i for v_i, w_i in zip(v, w))
dotV([1, 2, 3], [4, 5, 6])
32
벡터의 크기
벡터 \(v = [v_1, \cdots, v_n]\)가 주어졌을 때 벡터 \(v\)의 크기 \(\| v\|\)는 \(v\) 자신과의 내적의 제곱근이다.
Example 10.2
벡터 \([3, 4]\)의 크기는 다음과 같다.
벡터의 크기 계산 함수
제곱근은 math 모듈의 sqrt() 함수를 이용한다.
import math
def norm(v):
sum_of_squares = dotV(v, v)
return math.sqrt(sum_of_squares)
norm([3, 4])
5.0
10.2. 행렬#
행렬matrix은 숫자를 행과 열로 구성된 직사각형 모양으로 나열한 것이다.
\(n\) 개의 행과 \(k\) 개의 열로 구성된 행렬을 \(n \times k\) 행렬이라 부른다.
대부분의 프로그래밍 언어에서 행렬을 리스트의 리스트, 즉 2중 리스트로 구현한다.
예를 들어 아래 코드에서 A는 \(2 \times 3\) 행렬이고, B는 \(3 \times 2\) 행렬이다.
# 2x3 행렬
A = [[1, 2, 3],
[4, 5, 6]]
# 3x2 행렬
B = [[1, 2],
[3, 4],
[5, 6]]
행렬의 모양
\(n \times k\) 행렬의 모양shape을 \((n,k)\)로 표기한다. 예를 들어, \(1, 2, 3, 4, 5, 6\) 여섯 개의 항목을 가진 행렬의 모양은 네 종류인데, 이유는 6을 두 개의 양의 정수의 곱셈으로 표현하는 방법이 네 가지이기 때문이다.
(1, 6) 모양의 행렬: 한 개의 행과 여섯 개의 열
(2, 3) 모양의 행렬: 두 개의 행과 세 개의 열
(3, 2) 모양의 행렬: 세 개의 행과 두 개의 열
(6, 1) 모양의 행렬: 여섯 개의 행과 한 개의 열
아래 shape() 함수는 주어진 행렬의 모양을 튜플로 반환한다.
def shape(M):
"""
M: 행렬
M[i]의 길이가 일정하다고 가정
"""
num_rows = len(M) # 행의 수
num_cols = len(M[0]) # 열의 수
return num_rows, num_cols
shape(A)
(2, 3)
shape(B)
(3, 2)
행벡터와 열벡터
아래 그림은 행렬의 행과 열의 인덱스를 보여준다.
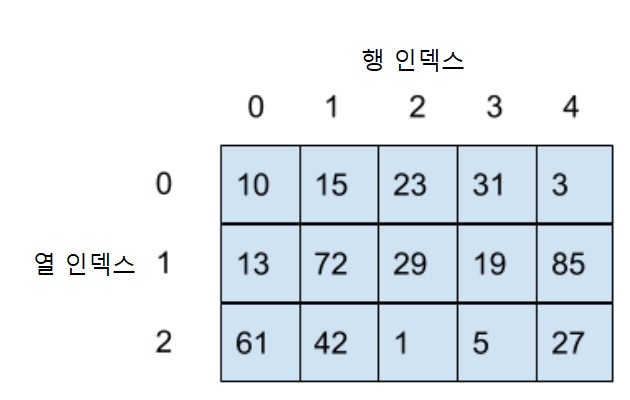
아래 두 함수는 각각 지정된 인덱스의 행과 지정된 인덱스의 열의 항목들로 구성된 행벡터와 열벡터를 반환한다.
# i번 행벡터
def get_row(M, i):
"""
M: 행렬
i: 행 인덱스
"""
return M[i]
# j번 열벡터
def get_column(M, j):
"""
M: 행렬
j: 열 인덱스
"""
return [M_i[j] for M_i in M]
행렬 A의 0번 행은 다음과 같다.
get_row(A, 0)
[1, 2, 3]
행렬 B의 1번 열은 다음과 같다.
get_column(B, 1)
[2, 4, 6]
\(i\) 행, \(j\) 열의 항목
행렬 \(M\)의 \(i\) 행, \(j\) 열의 항목은 \(i\) 번 인덱스 행의, \(j\) 번 인덱스 열에 위치한 값을 가리키며 \(M_{i, j}\)로 표기한다.
10.2.1. 행렬 초기화#
경우에 따라 0으로만, 1로만, 또는 임의의 수로 구성된 특정 모양의 행렬을 필요할 수 있다.
아래 make_matrix() 함수는 행렬의 항목을 생성하는 방식을 지정하면
원하는 모양의 행렬을 생성한다.
인자: 3개의 인자가 사용된다.
n: 행의 수m: 열의 수entry_fn: i, j가 주어지면 i행, j열에 위치한 항목 계산
반환값: 지정된 방식으로 계산된 (i, j) 모양의 행렬
def make_matrix(n, m, entry_fn):
"""
n: 행의 수
m: 열의 수
entry_fn: (i, j)에 대해 i행, j열에 위치한 항목 계산
"""
return [ [entry_fn(i, j) for j in range(m)] for i in range(n) ]
0-행렬
0-행렬zero matrix은 0으로 채워진 행렬이다. 아래 행렬은 (3, 2) 모양의 0-행렬이다.
지정된 모양의 0-행렬을 생성하는 함수는 다음과 같다.
def zeros(x):
"""
x = (n, m), 단 n, m은 양의 정수
"""
n = x[0]
m = x[1]
zero_function = lambda i, j: 0
return make_matrix(n, m, zero_function)
zeros((5,7))
[[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0]]
1-행렬
1-행렬one matrix이란 행렬의 모든 원소의 값이 1인 행렬을 말한다. 아래 행렬은 (3, 4) 모양의 1-행렬이다.
지정된 모양의 1-행렬을 생성하는 함수는 다음과 같다.
def ones(x):
"""
x = (n, m), 단 n, m은 양의 정수
"""
n = x[0]
m = x[1]
one_function = lambda i, j: 1
return make_matrix(n, m, one_function)
ones((5,7))
[[1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1]]
임의 행렬
임의 행렬random matrix은 행렬의 항목이 임의의 수로 구성된 행렬을 가리킨다.
여기서는 0과 1 사이의 임의의 수로만 구성된 임의 행렬을 생성한다.
이를 위해 random 모듈의 random() 함수를 이용한다.
import random
random.random() 함수는 [0, 1) 구간에서 임의의 수를 무작위로 반환한다.
random.random()
0.5670569975323919
random.random()
0.39145842242519246
지정된 모양의 임의 행렬을 생성하는 함수는 다음과 같다.
def rand(n, m):
"""
n, m: 양의 정수
"""
random_function = lambda i, j: random.random()
return make_matrix(n, m, random_function)
함수의 인자 형식
zeros() 함수와 ones() 함수는 행렬의 모양을 가리키는 튜플을 인자로 받는다.
반면에 rand() 함수는 행과 열의 크기 두 개의 인자를 받는다.
이는 나중에 다룰 넘파이 어레이에서 소개하는 넘파이 모듈에 포함된 동일한 이름의 함수들과
형식을 맞추기 위해서이다.
rand(5,3)
[[0.7079919633074715, 0.768254775291509, 0.002409901232759082],
[0.5364004790470274, 0.4798250929194987, 0.2734593220830823],
[0.777800238018411, 0.7354373309946959, 0.44950026103519214],
[0.1091465855777114, 0.7239775064936013, 0.8505189753481203],
[0.9656288013809685, 0.39406490949349227, 0.5456704281848319]]
부동소수점을 소수점 아래 몇 자리까지만 보이도록 하기 위해 round() 함수를 이용할 수 있다.
rand() 함수를 재정의 한다.
이때 항목을 생성하는 함수에 필요한 소수점 이하 자릿수를 ndigits=2 키워드 매개변수가
받도록 한다. 기본값은 2로 지정한다.
def rand(n, m, ndigits=2):
"""
n, m: 양의 정수
"""
random_function = lambda i, j: round(random.random(), ndigits) # ndigits: 소수점 이하 자릿수
return make_matrix(n, m, random_function)
소수점 이하 셋째 자리에서 반올림한 값을 사용하도록 하려면 기본 인자 2를 그대로 사용하면 되기에 굳이 셋째 인자를 지정할 필요가 없다.
rand(5, 3)
[[0.52, 0.34, 0.22],
[0.27, 0.69, 0.97],
[0.09, 0.23, 0.23],
[0.83, 0.82, 0.52],
[0.25, 0.44, 0.04]]
소수점 아래 다섯째 자리까지 보이도록 하려면 셋째 인자를 5로 지정한다.
rand(5, 3, 5)
[[0.98044, 0.20478, 0.04926],
[0.35022, 0.26039, 0.47058],
[0.70301, 0.67025, 0.73196],
[0.72061, 0.89882, 0.8883],
[0.98717, 0.27748, 0.23647]]
키워드 매개변수 이름을 함께 사용해도 된다.
rand(5, 3, ndigits=5)
[[0.58285, 0.41884, 0.72531],
[0.41466, 0.27118, 0.92179],
[0.87361, 0.13989, 0.671],
[0.1254, 0.21738, 0.9697],
[0.70894, 0.73182, 0.77568]]
항등행렬
항등행렬identity matrix은 정사각형 모양의 행렬 중에서 대각선 상에 위치한 항목은 1이고 나머지는 0인 행렬을 말한다. 예를 들어 아래 행렬은 (5, 5) 모양의 단위행렬이다.
단위행렬은 행과 열의 개수가 동일한 정방행렬이며, 지정된 모양의 단위행렬을 생성하는 함수는 다음과 같다.
def identity(n):
"""
n: 양의 정수
"""
one_function = lambda i, j: 1 if i == j else 0
return make_matrix(n, n, one_function)
identity(5)
[[1, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 0, 1]]
10.2.2. 행렬 항목별 연산#
행렬 항목별 덧셈
모양이 같은 두 행렬의 항목별 덧셈은 항목별로 더한 결과로 이루어진 행렬이다. \(2 \times 3\) 행렬의 항목별 덧셈은 다음과 같다.
행렬의 항목별 덧셈을 계산하는 함수는 다음과 같다.
def addM(A, B):
assert shape(A) == shape(B)
m, n = shape(A)
return make_matrix(m, n, lambda i, j: A[i][j] + B[i][j])
C = [[1, 3, 7],
[1, 0, 0]]
D = [[0, 0, 5],
[7, 5, 0]]
addM(C, D)
[[1, 3, 12], [8, 5, 0]]
행렬 항목별 뺄셈
모양이 같은 두 행렬의 항복별 뺄셈은 항목별로 뺀 결과로 이루어진 행렬이다. \(2 \times 3\) 행렬의 항목별 뺄셈은 다음과 같다.
행렬의 항목별 뺄셈을 계산하는 함수는 다음과 같다.
def subtractM(A, B):
assert shape(A) == shape(B)
m, n = shape(A)
return make_matrix(m, n, lambda i, j: A[i][j] - B[i][j])
subtractM(C, D)
[[1, 3, 2], [-6, -5, 0]]
행렬 스칼라 곱셈
숫자 하나와 행렬의 곱셈을 행렬 스칼라 곱셈이라 부른다. 스칼라 곱셈은 행렬의 각 항목을 지정된 숫자로 곱해 새로운 행렬을 생성한다. (2, 3) 모양의 행렬의 스칼라 곱셈은 다음과 같다.
행렬의 각 항목에 동일한 부동소수점을 곱한 결과를 반환하는 함수는 다음과 같다.
def scalar_multiplyM(c, M):
return [[c * row_i for row_i in row] for row in M]
scalar_multiplyM(2, C)
[[2, 6, 14], [2, 0, 0]]
10.2.3. 행렬 곱셈#
(\(m\), \(n\)) 모양의 \(A\)와 (\(n\), \(p\)) 모양의 행렬 \(B\)의 곱 \(A \cdot B\)는 (\(m\), \(p\)) 모양의 행렬이며, \(i\) 행, \(j\) 열의 항목 \((A \cdot B)_{i,j}\)는 다음과 같이 정의된다.
아래 그림으로 (4, 2) 모양의 행렬 \(A\)와 (2, 3) 모양의 행렬 \(B\)의 점곱인 \(A\cdot B\)의 항목을 계산하는 과정을 보여준다.
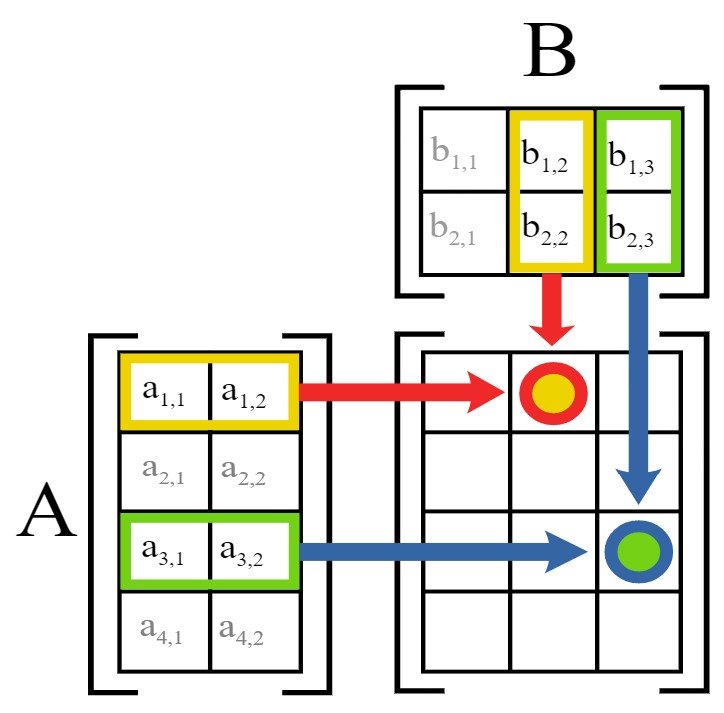
출처: 위키백과
예를 들어 \(2 \times 3\) 행렬과 \(3 \times 2\) 행렬의 곱셈은 다음과 같다.
행렬의 곱셈을 계산하는 함수는 다음과 같다. 2중 리스트 조건제시법을 사용하면 간단하게 구현할 수 있다.
A: (m, n) 모양의 행렬(2중 리스트)B가 (n, p) 모양의 행렬(2중 리스트)*B: 리스트 풀어헤치기의 결과. 차원이 p인 리스트 n개.zip(*B): 차원이 n인 열벡터 p개.
def matmul(A, B):
"""
A: (m, n) 모양의 행렬(2중 리스트)
B: (n, p) 모양의 행렬(2중 리스트)
"""
mat_mul = [[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] for A_row in A]
return mat_mul
# 3x2 행렬
A = [[2, 7],
[4, 5],
[7, 8]]
# 2x4 행렬
B = [[5, 8, 1, 2],
[4, 5, 9, 1]]
matmul(A, B)
[[38, 51, 65, 11], [40, 57, 49, 13], [67, 96, 79, 22]]
행렬 곱셈의 항등원
임의의 행렬 \(M\)과 항등행렬과의 곱은 \(M\) 자신이다. 즉 항등행렬은 행렬 곱셈의 항등원이다.
# 3x2 행렬
M = [[3, 1],
[2, 1],
[1, 0]]
matmul(M, identity(2)) == M
True
10.2.4. 전치행렬#
행렬의 전치란 행과 열을 바꾸는 것으로, 행렬 \(A\)의 전치는 \(A^T\)로 표기한다. 즉, \(A\)가 (\(m\), \(n\)) 모양의 행렬이면 \(A^T\)는 (\(n\), \(m\)) 모양의 행렬이다. \(A^T\)의 \(i\)행의 \(j\)열번째 값은 \(A\)의 \(j\)행의 \(i\)열번째 값이다. 즉 다음이 성립한다.
예를 들어, 다음은 (2, 3) 모양의 행렬의 전치가 (3, 2) 모양의 행렬이 됨을 잘 보여준다.
전치 행렬을 계산하는 함수는 다음과 같다.
def transpose(M):
"""
M: (m, n) 모양의 행렬
"""
return [list(col) for col in zip(*M)]
X = [[9, 8, 7],
[-1, 3, 4]]
transpose(X)
[[9, -1], [8, 3], [7, 4]]
전치행렬의 성질
\(a\)를 스칼라, \(A\)와 \(B\)를 크기가 같은 행렬이라 하자. 이때 다음이 성립한다.
\((A^T)^T = A\)
\((A + B)^T = A^T + B^T\)
\((A - B)^T = A^T - B^T\)
\((a\cdot A)^T = a\cdot A^T\)
\((A\cdot B)^T = B^T \cdot A^T\)
A
[[2, 7], [4, 5], [7, 8]]
B
[[5, 8, 1, 2], [4, 5, 9, 1]]
transpose(transpose(A)) == A
True
C
[[1, 3, 7], [1, 0, 0]]
D
[[0, 0, 5], [7, 5, 0]]
transpose(addM(C, D)) == addM(transpose(C), transpose(D))
True
transpose(subtractM(C, D)) == subtractM(transpose(C), transpose(D))
True
transpose(scalar_multiplyM(2, A)) == scalar_multiplyM(2, transpose(A))
True
transpose(matmul(A, B)) == matmul(transpose(B), transpose(A))
True
10.3. 연습문제#
참고: (실습) 선형대수 기초
