16. 실전 예제: 붓꽃 데이터 분석#
주요 내용
예제: 그래프 배경색칠
예제: 붓꽃 데이터셋 분석
기본 설정
numpy 모듈과 시각화 도구 모듈인 matplotlib.pyplot에 대한 기본 설정을 지정한다.
# 넘파이
import numpy as np
# 램덤 시드
np.random.seed(12345)
# 어레이 사용되는 부동소수점들의 정확도 지정
np.set_printoptions(precision=4, suppress=True)
# 파이플롯
import matplotlib.pyplot as plt
# # 도표 크기 지정
# plt.rc('figure', figsize=(10, 6))
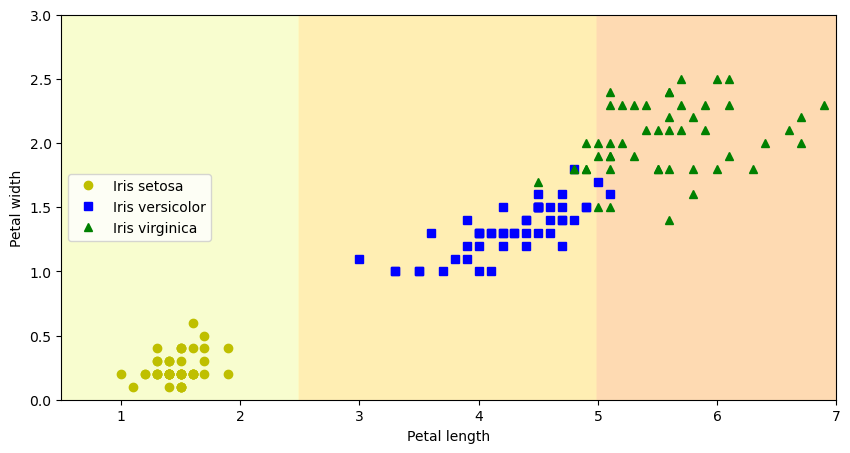
16.1. 목표#
최종적으로 아래와 같은 산점도를 그리려 한다. 각각의 점들은 붓꽃(아이리스) 데이터셋에 포함된 150개의 데이터 샘플을 세 개의 품종에 따라 다른 색깔과 모양으로 보여준다. 또한 품종을 구분하는 두 개의 직선을 경계로 배경색을 달리한다.
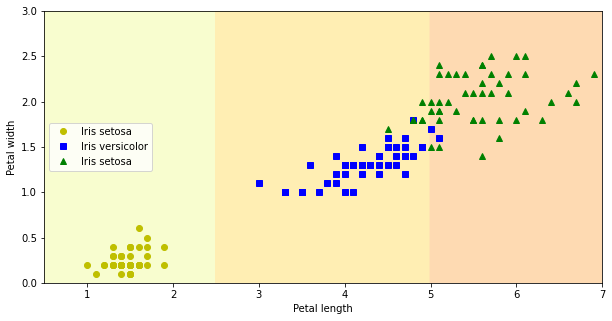
먼저 배경을 색칠하는 방법을 알아본다.
16.2. 그래프 배경 색칠#
그래프 배경으르 그리는 방법은 아래와 같은 격자 무늬에 사용되는 점들을 2차원 어레이를 이용하여 사람의 눈으로 구분할 수 없을 정도로 촘촘하게 그리는 것이다.
16.2.1. 2차원 격자 어레이#
아래 모양의 회색 격자무늬를 그리기 위해 필요한 2차원 어레이를 생성하고자 한다. 각 점의 좌표는 -1과 1사이의 값을 10개의 구간으로 균등하게 나눈 값들이다. 즉, 가로 세로 모두 11개의 점으로 구성된다.
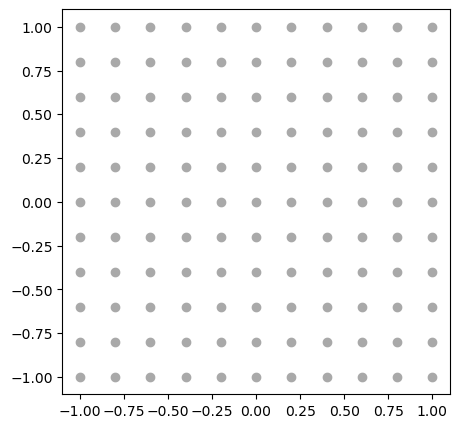
먼저 np.arange() 함수를 이용하여 -1와 1 사이의 구간을 10개의 구간으로 균등하게
나누는 어레이를 생성하려면
아래에서 처럼 -1에서 1.01 이전까지 0.2 스텝으로 증가하는 값들로 이루어진 어레이를 생성하면 된다.
points = np.arange(-1, 1.01, 0.2)
points
array([-1. , -0.8, -0.6, -0.4, -0.2, -0. , 0.2, 0.4, 0.6, 0.8, 1. ])
np.meshgrid() 함수
예를 들어 matplotlib.pyplot 모듈의 scatter() 함수를 이용하여 위 그림에 있는 총 121(= 11 \(\times\) 11)개의 점을
산점도로 그리려면 각각 121개의 x-좌표와 y-좌표를 담은 두 개의 리스트가 필요하다.
np.meshgrid() 함수를 이용하면 손쉽게 두 리스트를 구할 수 있다.
np.meshgrid() 함수는 지정된 1차원 어레이 두 개를 이용하여 그릴 수 있는 격자무늬의
x-좌표 리스트와 y-좌표 리스트를 생성하며
아래와 같이 실행한다.
xs, ys = np.meshgrid(points, points)
xs는 행별x-좌표를 2차원 어레이로 담고 있다.
행별로 x-좌표는 작은 값에서 큰 값으로,
행의 순서 또한 작은 값에서 큰 값으로 변한다.
xs
array([[-1. , -0.8, -0.6, -0.4, -0.2, -0. , 0.2, 0.4, 0.6, 0.8, 1. ],
[-1. , -0.8, -0.6, -0.4, -0.2, -0. , 0.2, 0.4, 0.6, 0.8, 1. ],
[-1. , -0.8, -0.6, -0.4, -0.2, -0. , 0.2, 0.4, 0.6, 0.8, 1. ],
[-1. , -0.8, -0.6, -0.4, -0.2, -0. , 0.2, 0.4, 0.6, 0.8, 1. ],
[-1. , -0.8, -0.6, -0.4, -0.2, -0. , 0.2, 0.4, 0.6, 0.8, 1. ],
[-1. , -0.8, -0.6, -0.4, -0.2, -0. , 0.2, 0.4, 0.6, 0.8, 1. ],
[-1. , -0.8, -0.6, -0.4, -0.2, -0. , 0.2, 0.4, 0.6, 0.8, 1. ],
[-1. , -0.8, -0.6, -0.4, -0.2, -0. , 0.2, 0.4, 0.6, 0.8, 1. ],
[-1. , -0.8, -0.6, -0.4, -0.2, -0. , 0.2, 0.4, 0.6, 0.8, 1. ],
[-1. , -0.8, -0.6, -0.4, -0.2, -0. , 0.2, 0.4, 0.6, 0.8, 1. ],
[-1. , -0.8, -0.6, -0.4, -0.2, -0. , 0.2, 0.4, 0.6, 0.8, 1. ]])
ys는 행별 y-좌표를 2차원 어레이로 담고 있다.
행별로 x-좌표는 작은 값에서 큰 값으로,
행의 순서 또한 작은 값에서 큰 값으로 변한다.
ys
array([[-1. , -1. , -1. , -1. , -1. , -1. , -1. , -1. , -1. , -1. , -1. ],
[-0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8, -0.8],
[-0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6, -0.6],
[-0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4, -0.4],
[-0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2, -0.2],
[-0. , -0. , -0. , -0. , -0. , -0. , -0. , -0. , -0. , -0. , -0. ],
[ 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.2],
[ 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4, 0.4],
[ 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6],
[ 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8, 0.8],
[ 1. , 1. , 1. , 1. , 1. , 1. , 1. , 1. , 1. , 1. , 1. ]])
xs와 ys를 이용하여 산점도를 그리면 원하는 격자무늬가 얻어진다.
c='darkgray'또는color='darkgray': 산점도에 사용되는 점들의 색상 지정. 여기서는 darkgray 사용. 보다 다양한 색상 정보는 Matplotlib Scatter 참고.
# 도표 크기 지정
plt.rc('figure', figsize=(5, 5))
# 산점도 그리기
plt.scatter(xs, ys, c='darkgray')
plt.show()
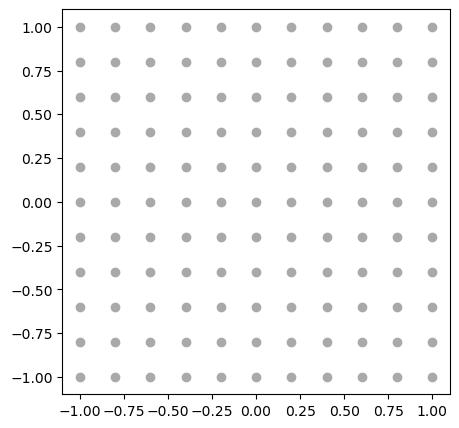
16.2.2. 배경색칠#
예를 들어 회색 배경을 얻고자 한다면 보다 점을 보다 촘촘히 찍으면 된다. 예를 들어, -1부터 1사이의 구간은 0.02 크기로 총 100개의 구간으로 구성한 다음에 동일한 그래프를 그리면 훨씬 더 섬세한 사진을 얻는다.
points = np.arange(-1, 1.01, 0.02)
meshgrid() 함수를 이용하여 메쉬 생성에 필요한 x 좌표와 y 좌표 모음을 만든다.
xs, ys = np.meshgrid(points, points)
xs 와 ys 각각 (101, 101) 모양의 2차원 어레이다.
xs.shape
(101, 101)
ys.shape
(101, 101)
xs와 ys를 이용하여 산점도를 그리면 한 장의 회색 색종이를 얻는다. 이유는 픽셀이 촘촘하기 때문이다.
# 도표 크기 지정
plt.rc('figure', figsize=(6, 6))
# 산점도 그리기
plt.scatter(xs, ys, c'darkgray')
plt.show()
배경색은 c의 키워드 인자를 변경하면 된다.
예를 들어, 연노랑 배경을 원하면 c='lightyello' 옵션을 지정한다.
# 도표 크기 지정
plt.rc('figure', figsize=(6, 6))
# 산점도 그리기
plt.scatter(xs, ys, c='lightyellow')
plt.show()
16.2.3. 등고선#
등고선 기능을 이용하여 배경색을 구역에 따라 다르게 할 수 있다. 등고선을 그리려면 먼저 배경을 포함되는 각각의 점의 좌표에 따라 값을 달리하는 방법을 지정해야 한다.
예를 들어 원점으로부터 멀어질 수록 색을 달리하는 등고선을 그리기 위해
xs와 ys에 대해 원의 방정식을 적용한다.
참고로 원점을 중심으로 하고, 반지름이 \(r\)인 원에 포함되는 점들의 좌표 \((x, y)\)는 다음 방정식을 만족해야 한다.
따라서 \(\sqrt{x^2 + y^2}\)의 값에 따라 해당 점이 원점으로부터의 거리를 가리키며, 이 성질을 이용하여 배경에 사용되는 각 점의 원점으로부터의 거리에 따라 배경색을 달리할 수 있다.
아래 코드가 배경에 사용되는 각각의 점에 대해 원점으로부터의 거리를 계산한다.
z = np.sqrt(xs ** 2 + ys ** 2)
z.shape
(101, 101)
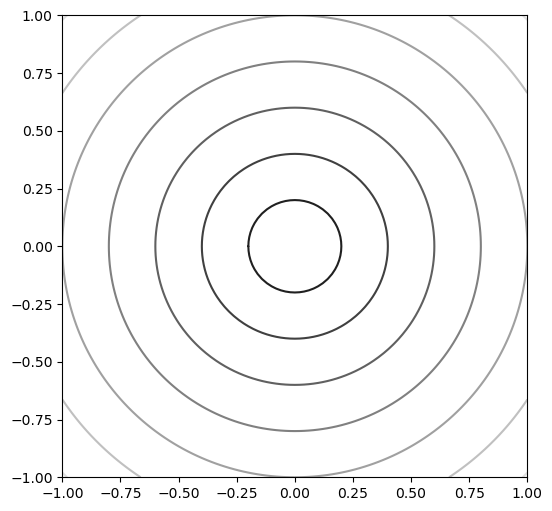
이제 plt.contour() 함수를 z 값을 기준으로 등고선을 흑백사진으로 그리게 하면 다음과 같다.
# 도표 크기 지정(기본값으로 되돌림)
plt.rc('figure', figsize=(6, 6))
plt.contour(xs, ys, z, cmap='gray')
plt.show()
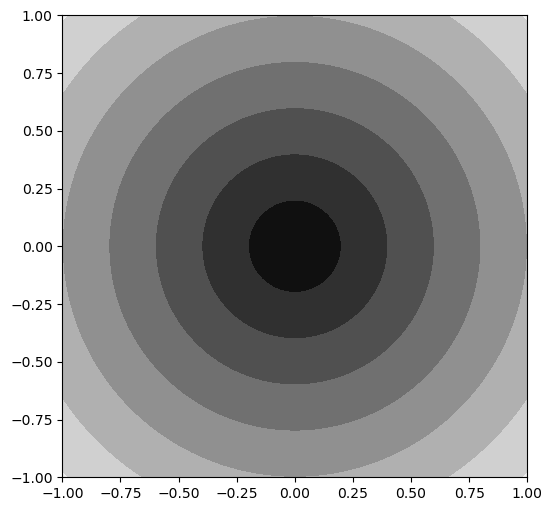
plt.contourf() 함수는 등고선에 의해 구분된 영역을 z 값에 따른 색을 칠한다.
plt.rc('figure', figsize=(6, 6))
plt.contourf(xs, ys, z, cmap='gray')
plt.show()
다양한 색지도를
이용하여 자신만의 색상으로 배경을 색칠할 수 있다.
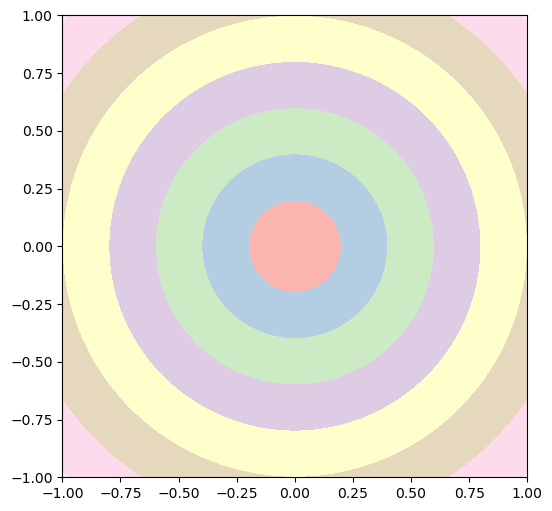
아래 코드는 예를 들어 파스텔 색지도인 Pastel1을 이용한다.
plt.rc('figure', figsize=(6, 6))
plt.contourf(xs, ys, z, cmap='Pastel1')
plt.show()
16.3. 붓꽃 데이터 분석#
16.3.1. 데이터셋 불러오기#
붓꽃(아이리스) 데이터를 이용하여 활용법을 살펴 보기 위해 먼저 데이터를 인터넷 상에서 가져온다.
url = 'https://raw.githubusercontent.com/codingalzi/datapy/master/jupyter-book/data/iris_nan.data'
# url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
위 주소의 iris.data 파일을 data라는 하위 디렉토리에 저장한다.
from pathlib import Path
import urllib.request
data_path = Path() / "data"
data_path.mkdir(parents=True, exist_ok=True)
urllib.request.urlretrieve(url, data_path / 'iris.data')
(PosixPath('data/iris.data'), <http.client.HTTPMessage at 0x7f5ab39e5050>)
다운로드된 iris.data 파일에는 아래 형식의 데이터가 150개 들어 있다.
5.1,3.5,1.4,0.2,Iris-setosa
하나의 데이터에 사용된 값들은 하나의 아이리스(붓꽃)에 대한 꽃잎, 꽃받침과 관련된 특성(features)과 품종을 나타내며, 보다 구체적으로 아래 순서를 따른다.
꽃받침 길이, 꽃받침 너비, 꽃잎 길이, 꽃잎 너비, 품종
이 중에 마지막 품종 특성은 문자열이고 나머지 특성은 부동소수점, 즉 수치형 데이터이다. 아래 사진은 붓꽃의 꽃받침sepal과 꽃잎petal의 길이와 너비를 측정하는 방법을 보여준다.

여기서는 연습을 위해 수치형 데이터를 담고 있는 네 개의 특성만 가져온다.
genfromtxt()함수: 인터넷 또는 컴퓨터에 파일로 저장된 데이터를 적절한 모양의 어레이로 불러오는 함수delimiter=',': 쉼표를 특성값들을 구분하는 기준으로 지정dtype='float': 어레이의 항목을 부동소수점으로 지정usecols=[0,1,2,3]: 리스트에 지정된 인덱스의 특성만 가져오기
iris_features = np.genfromtxt(data_path / 'iris.data', delimiter=',', dtype='float', usecols=[0,1,2,3])
어레이의 모양은 (150, 4)이다.
iris_features.shape
(150, 4)
처음 5개 샘플은 다음과 같다.
iris_features[:5]
array([[5.1, 3.5, 1.4, 0.2],
[4.9, 3. , 1.4, 0.2],
[4.7, 3.2, 1.3, 0.2],
[4.6, 3.1, 1.5, 0.2],
[5. , 3.6, 1.4, 0.2]])
16.3.2. 결측치 처리#
붓꽃 데이터셋 안에 결측치가 포함되어 있다. 결측치가 있는지 여부를 다음과 같이 확인한다.
np.isnan()함수: 어레이의 각각의 항목이 결측치인지 여부를 확인하는 부울 어레이 반환any()어레이 메서드: 부울 어레이의 항목에True가 하나라도 포함되어 있는지 여부 확인
np.isnan(iris_features).any()
True
결측치가 특정 열에만 있는지를 확인하려면 축을 0으로 지정한다.
np.isnan(iris_features).any(axis=0)
array([False, False, False, True])
3번 열에만 결측치가 있음이 확인됐다.
sum() 함수를 이용하여 3개의 결측치가 있음을 바로 확인할 수 있다.
sum()어레이 메서드:True는 1,False는 0으로 처리한다.
np.isnan(iris_features).sum()
3
3번 열에만 결측치가 있기에 아래와 같이 결측치의 수를 확인할 수도 있다.
np.isnan(iris_features[:, 3]).sum()
3
부울 인덱싱을 활용하여 결측치가 없는 행만 추출할 수 있으며, 결측치를 포함한 데이터 샘플 3개는 다음과 같다.
mask = np.isnan(iris_features[:, 3])
iris_features[mask]
array([[5.4, 3.4, 1.7, nan],
[5. , 3.2, 1.2, nan],
[4.4, 3.2, 1.3, nan]])
nan은 결측치를 의미하는 값인 np.nan을 가리키는 기호다.
np.nan
nan
원본 iris_nan.data 파일에서 결측치는 아래와 같이 그냥 비워져 있다.
5.4, 3.4, 1.7,, Iris-setosa
5. , 3.2, 1.2,, Iris-setosa
4.4, 3.2, 1.3,, Iris-setosa
그런데 3개의 결측치는 사실 일부러 만들어졌고 원래 모두 0.2였다. 부울 인덱싱을 이용하여 결측치를 모두 0.2로 원상회복 시킨다.
iris_features[:, 3][mask] = 0.2
결측치가 없음을 다음과 같이 확인한다.
np.isnan(iris_features).any()
False
품종 정보
iris_features 데이터셋에 사용된 붓꽃들의 품종은 아래 세 개이다.
'Iris-setosa', 'Iris-versicolor', 'Iris-virginica'
이 사실을 데이터셋에서 직접 확인할 수 있다.
usecols=4: 품종 정보를 담고 있는 열만 가져오기dtype='str: 문자열로 처리
iris_labels = np.genfromtxt(data_path / 'iris.data', delimiter=',', dtype='str', usecols=4)
길이가 150인 1차원 어레이로 가져온다.
iris_labels.shape
(150,)
사용되는 품종이 3가지임을 np.unique() 함수를 이용해서 확인한다.
varieties = np.unique(iris_labels)
varieties
array(['Iris-setosa', 'Iris-versicolor', 'Iris-virginica'], dtype='<U15')
품종별로 각각 50개의 샘플이 포함된다.
for variety in varieties:
count = np.count_nonzero(iris_labels == variety)
print(f"{variety:<15} 샘플 수: {count}")
Iris-setosa 샘플 수: 50
Iris-versicolor 샘플 수: 50
Iris-virginica 샘플 수: 50
16.3.3. 산점도 그리기#
꽃잎의 길이(2번 열)와 너비 정보(3번 열)를 이용하여 산점도를 그린다. 먼저 꽃잎 길이를 x-좌표값으로, 꽃잎 너비를 y-좌표 값으로 지정한다. 이때 모든 x-좌표와 모든 y-좌표를 따로따로 지정한다.
X = iris_features[:, 2] # 꽃잎 길이
Y = iris_features[:, 3] # 꽃잎 너비
plt.plot() 함수를 이용하여 산점도를 그릴 수 있다.
셋째 인자:
"bo"는 점의 색깔과 모양 지정.b는 blue(파랑)를,o는 동그라미 모양의 점.plt.plot(X, Y, "bo")는plt.plot(X, Y, color='blue', marker='o', linesty;e='')를 줄인 표현plt.axis([0.5, 7, 0, 3]): x-축 구간은 0.5부터 7, y-축 구간은 0부터 3.
plt.figure(figsize=(10, 5))
plt.plot(X, Y, 'bo')
# plt.plot(X, Y, color='blue', marker='o', linestyle='')
plt.axis([0.5, 7, 0, 3])
(0.5, 7.0, 0.0, 3.0)
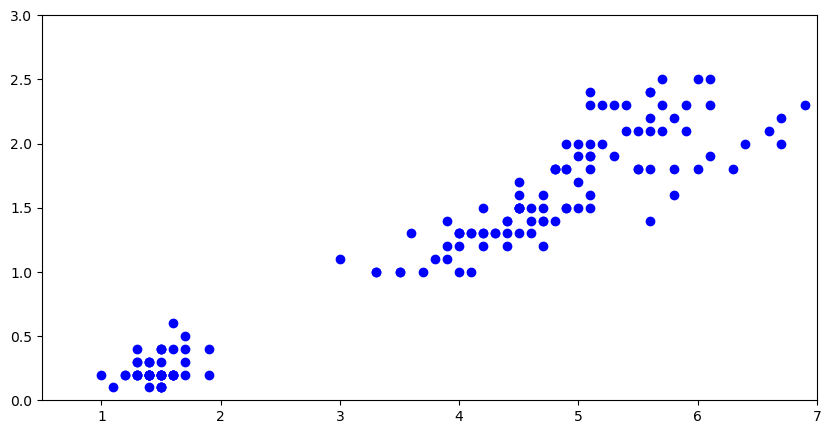
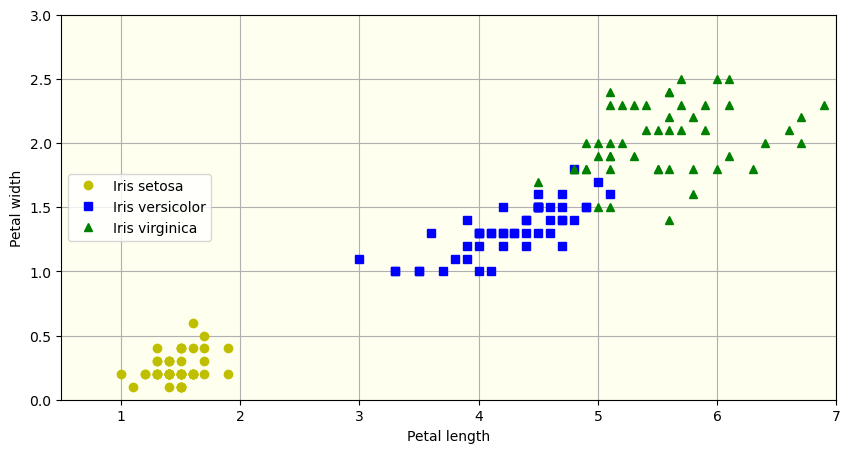
그런데 이렇게 하면 품종이 구별되지 않기에 품종 정보를 함께 활용해야 한다. 예를 들어 세토사 품종 50개의 꽆잎의 길이는 다음과 같이 부울 마스크를 이용해서 구할 수 있다.
plt.xlabel("Petal length"): x-축 레이블 지정plt.ylabel("Petal width"): y-축 레이블 지정plt.legend(loc="center left"): 범례 위치 지정plt.show(): 여러 개의 그래프를 동시에 하나의 캔버스에 그리도록 함
plt.figure(figsize=(10, 5))
# 세토사 품종 산점도: 노랑 동그라미
plt.plot(X[iris_labels == 'Iris-setosa'], Y[iris_labels == 'Iris-setosa'], 'yo', label='Iris setosa')
# 버시컬러 품종 산점도: 파랑 네모
plt.plot(X[iris_labels == 'Iris-versicolor'], Y[iris_labels == 'Iris-versicolor'], 'bs', label='Iris versicolor')
# 버지니카 품종 산점도: 초록 세모
plt.plot(X[iris_labels == 'Iris-virginica'], Y[iris_labels == 'Iris-virginica'], 'g^', label='Iris virginica')
plt.xlabel("Petal length")
plt.ylabel("Petal width")
plt.legend(loc="center left")
plt.axis([0.5, 7, 0, 3.])
plt.show()
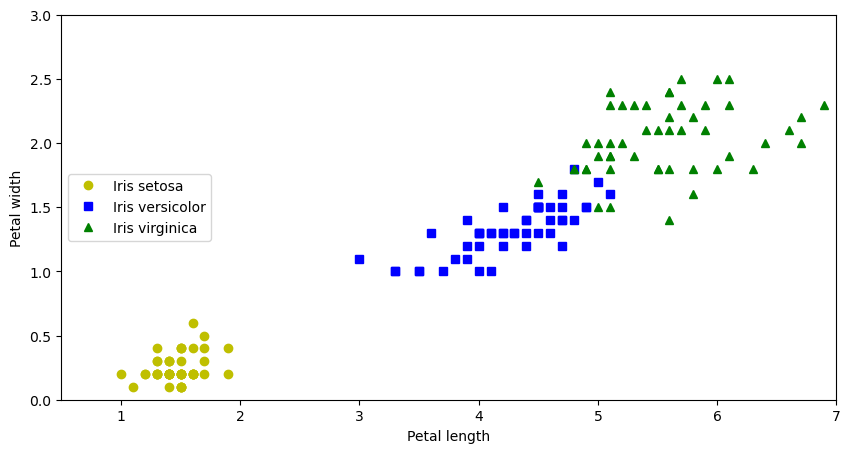
격자 무늬
격자 무늬 배경도 넣을 수 있다.
plt.grid(): 격차 무늬 배경 추가
plt.figure(figsize=(10, 5))
plt.plot(X[iris_labels == 'Iris-setosa'], Y[iris_labels == 'Iris-setosa'], 'yo', label='Iris setosa')
plt.plot(X[iris_labels == 'Iris-versicolor'], Y[iris_labels == 'Iris-versicolor'], 'bs', label='Iris versicolor')
plt.plot(X[iris_labels == 'Iris-virginica'], Y[iris_labels == 'Iris-virginica'], 'g^', label='Iris virginica')
plt.xlabel("Petal length")
plt.ylabel("Petal width")
plt.legend(loc="center left")
plt.axis([0.5, 7, 0, 3.])
plt.grid()
plt.show()
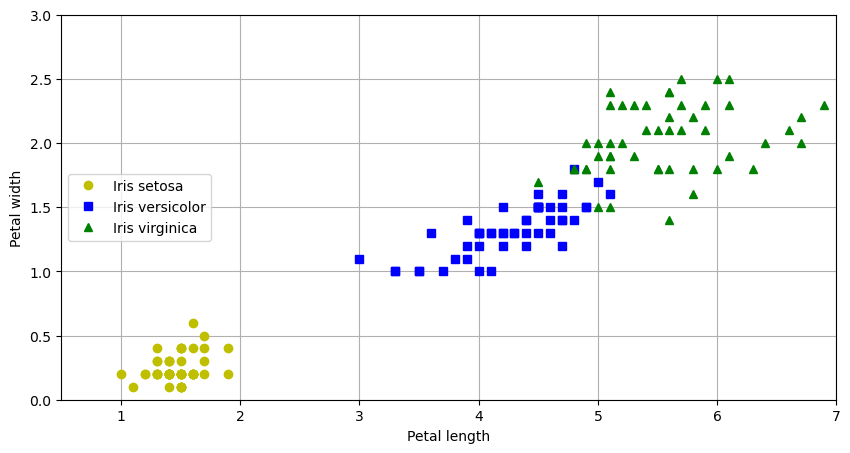
16.3.4. 배경 색칠#
meshgrid() 함수를 이용하여 배경의 색을 지정할 수 있다.
points_x = np.arange(0, 7.01, 0.02)
points_y = np.arange(0, 3.51, 0.02)
xs, ys = np.meshgrid(points_x, points_y)
plt.figure(figsize=(10, 5))
# 배경
plt.scatter(xs, ys, c= 'ivory') # 아이보리색
# 붓꽃 데이터 산점도
plt.plot(X[iris_labels == 'Iris-setosa'], Y[iris_labels == 'Iris-setosa'], 'yo', label='Iris setosa')
plt.plot(X[iris_labels == 'Iris-versicolor'], Y[iris_labels == 'Iris-versicolor'], 'bs', label='Iris versicolor')
plt.plot(X[iris_labels == 'Iris-virginica'], Y[iris_labels == 'Iris-virginica'], 'g^', label='Iris virginica')
plt.xlabel("Petal length")
plt.ylabel("Petal width")
plt.legend(loc="center left")
plt.axis([0.5, 7, 0, 3.])
plt.grid()
plt.show()
16.3.5. 등고선과 품종 분류#
품종의 분류를 색으로 구분하기 위해 plt.contour() 함수 또는 plt.contourf() 를 이용한다.
적절한 등고선을 그리기 위해 meshgrid() 함수가 생성한 각 좌표에 해당하는 지점의
값을 담고 있는 어레이 Z를 생성한다.
단 x-좌표의 값에 따라 0, 1, 2를 항목으로 갖도록 한다.
0: x-좌표가 2.5보다 작은 경우
1: x-좌표가 2.5보다 같거나 크고 5보다 작은 경우
2: x-좌표가 5보다 같거나 큰 경우
먼저 xs, ys와 동일한 모양을 갖는 0-행렬로 Z를 생성한다.
Z = np.zeros(xs.shape)
이제 배경에 포함된 점들의 x-좌표값이 2.5와 5를 기준으로 Z의 항목에 해당하는 값을 각각 1과 2로 변경한다.
아래 코드는 부울 마스크를 이용하여 이 과정을 처리한다.
Z[(2.5 <= xs) & (xs < 5)] = 1
Z[(5. <= xs)] = 2
Z
array([[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]])
아래 코드는 다른 색의 등고선을 이용하여 자연스럽게 품종을 구분하는 배경과 함께 산점도를 그린다. 배경을 먼저 그린 다음에 산점도를 그림에 주의한다.
plt.contourf(xs, ys, Z, alpha=0.3, cmap='Wistia'): 색으로 등고선 구분.alpha=0.3: 투명도를 0.3으로 지정. 0에서 1사이의 값이며 클 수록 불투명해짐cmap='Wistia: 등고선에 사용할 색 지도 지정
plt.figure(figsize=(10, 5))
# 등고선을 색으로 구분
plt.contourf(xs, ys, Z, alpha=0.3, cmap='Wistia')
# 붓꽃 데이터 산점도
plt.plot(X[iris_labels == 'Iris-setosa'], Y[iris_labels == 'Iris-setosa'], 'yo', label='Iris setosa')
plt.plot(X[iris_labels == 'Iris-versicolor'], Y[iris_labels == 'Iris-versicolor'], 'bs', label='Iris versicolor')
plt.plot(X[iris_labels == 'Iris-virginica'], Y[iris_labels == 'Iris-virginica'], 'g^', label='Iris virginica')
plt.xlabel("Petal length")
plt.ylabel("Petal width")
plt.legend(loc="center left")
plt.axis([0.5, 7.0, 0, 3])
# plt.grid()
plt.show()