11. 재귀 시각화#
슬라이드
본문 내용을 요약한 슬라이드를 다운로드할 수 있다.
주요 내용
재귀 시각화
꼬리 재귀 일반화
11.1. 재귀 시각화#
재귀를 이해하기 위해 재귀 알고리즘의 작동과정을 시각화햅보자.
시각화를 위해 turtle 모듈을 이용한다.
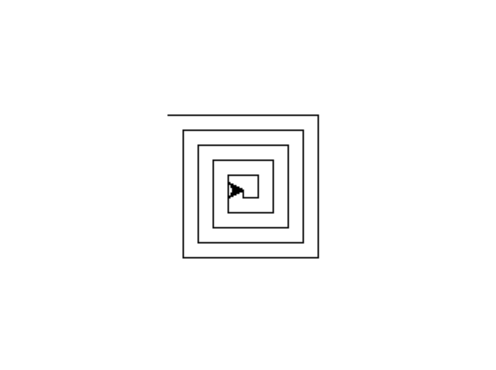
예를 들어, draw_spiral() 함수는 아래 그림과 같은 소용돌이를 그린다.
주의사항: turtle 모듈을 사용하는 코드를 주피터 노트북 또는 구글 코랩에서 실행하려면
특별한 모듈을 설치해야 한다.
여기서는 대신에 개인 피씨 환경 또는 Repl.it 사이트에서 코드를 실행할 것을 권장한다.
이런 이유로 이어지는 코드는 텍스트셀로 제공된다.
import turtle
def draw_spiral(my_turtle, line_len):
if line_len > 0:
my_turtle.forward(line_len)
my_turtle.right(90)
draw_spiral(my_turtle, line_len - 5)
my_turtle = turtle.Turtle()
my_win = turtle.Screen()
draw_spiral(my_turtle, 100)
my_win.exitonclick()
예제: 프랙탈 트리
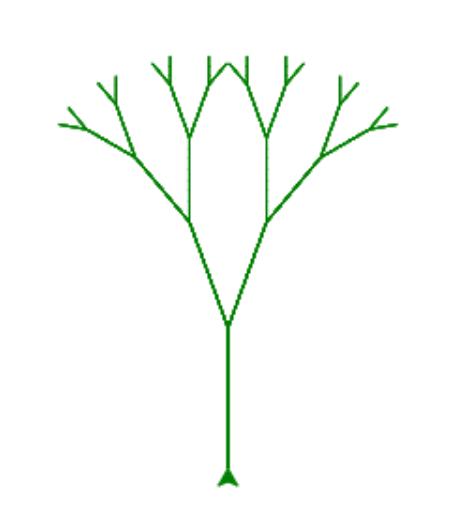
아래 이미지처럼 아무리 확대하더라도 항상 동일한 구조를 보여주는 사물이 프랙탈(fractal)이다.

프랙탈의 구조는 재귀와 매우 밀접한 관계를 갖는다.
예를 들어, tree() 함수는 아래 모양의 프랙탈 트리를 그린다.
참고: Repl.it: 프랙탈 트리에서
실행할 수 있다.
pythonds3: 5.7 Introduction: Visualizing Recursion를 이용할 경우 time.sleep() 함수를 추가하여 천천히 실행되는 재귀 알고리즘의 작동을 살펴볼 수 있다.
import turtle
# import time # 주의: repl.it 사이트에서 오류 발생
def tree(branch_len, t):
if branch_len > 5: # 종료조건: branch_len <= 5
t.forward(branch_len) # 전진
# time.sleep(1)
t.right(20) # 오른쪽 가지치기
tree(branch_len - 15, t)
t.left(40) # 왼쪽 가지치기
tree(branch_len - 15, t)
t.right(20) # 한 단계 후진
t.backward(branch_len)
t = turtle.Turtle()
my_win = turtle.Screen()
t.left(90)
t.up()
t.backward(100)
t.down()
t.color("green")
tree(75, t)
my_win.exitonclick()
tree() 함수는 오른쪽 가지를 먼저 그리며, 이 과정을 최대한 멀리 진행한다.
가지치기를 할 때마다 가지의 길이를 15씩 줄이며,
그려야 할 가지의 길이가 5 이하일 때 가지치기를 멈춘다.
아래 이미지는 가지의 길이를 처음에 75로 시작해서 5번 오른쪽 가지치기를 수행한 후
더 이상의 가지치기가 불가능한 상태를 보여준다.

더 이상 오른쪽 가지치기가 불가능하면 뒤로 한 단계 후진한 다음에 왼쪽 가지치기를 진행한다. 왼쪽 가지치기 이후 오른쪽 가지치가 가능하면 이를 먼저 수행한다. 아래 이미지는 그려야할 프랙탈 트리의 절반을 그린 상태를 보여준다.

11.2. 꼬리 재귀 일반화#
리스트에 포함된 항목들의 합을 계산하는 list_sum()의 실행과정을 이해하기
위해 사용된 머리(head)와 꼬리(tail) 개념을 많은 재귀 알고리즘에 적용할 수 있다.
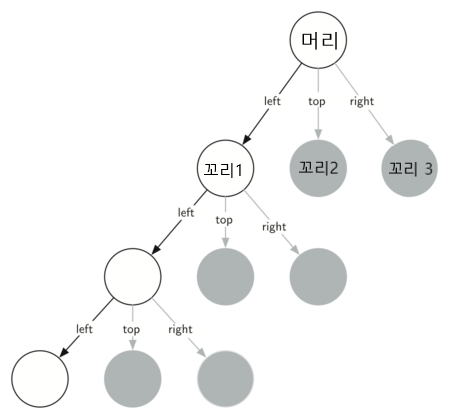
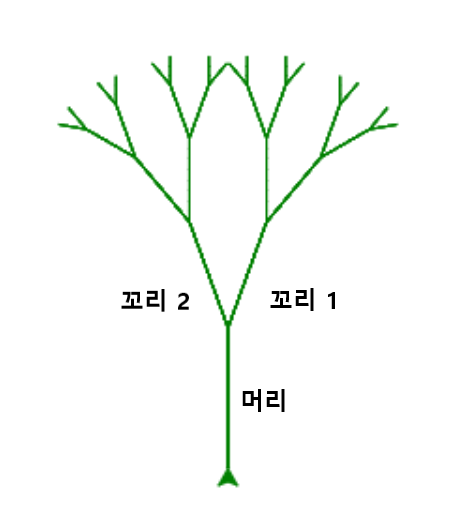
프랙탈 트리의 경우 가지 하나를 그린 다음 가지치기가 이루어지며 가지치기 이후에는 동일한 과정이 반복된다. 다만, 좌우 각 가지에서 완성되는 프랙탈 트리는 완성되어야 하는 전체 프랙탈 트리의 일부분을 담당한다. 그려진 하나의 가지를 머리, 그려져야 하는 좌우 두 개의 가지를 두 개의 꼬리로 이해할 수 있다. 즉, 머리를 그린 다음에 나머지는 각각의 꼬리에 동일한 과제를 떠넘기는 과정의 연속이 된다(아래 그림 참조).
예제: 시에르핀스키 삼각형Sierpinski Triangle
정삼각형을 4등분한 후에 가장자리에 위치한 세 개의 삼각형을 대상으로 4등분하는 과정을 무한반복하여 얻어지는 삼각형이 시에르핀스키(Sierpinski) 삼각형이며 이 또한 프랙탈이다.

머리와 꼬리를 이용한 재귀 알고리즘의 이해는 시에르핀스키 삼각형을 이해할 때도 기본적으로 동일하게 적용된다.
머리: 하나의 삼각형 그리기
꼬리: 4등분 후 각 꼭지점에서 동일한 과정 반복하기. 즉, 3 개의 꼬리 사용.
시에르핀스키 삼각형 그리기를 재귀 알고리즘으로 구현하면 다음과 같다.
참고: Repl.it: 시에르핀스키 삼각형에서
실행할 수 있다.
pythonds3: 5.8 Sierpinski Triangle를 이용할 경우
아래 코드에 time.sleep() 함수를 추가하여 천천히 실행되는 재귀 알고리즘의 작동을 살펴볼 수 있다.
import turtle
# import time # 주의: repl.it 사이트에서 오류 발생
# 삼각형 그리기
def draw_triangle(points, color, my_turtle):
my_turtle.fillcolor(color)
my_turtle.up()
my_turtle.goto(points[0][0], points[0][1])
my_turtle.down()
my_turtle.begin_fill()
my_turtle.goto(points[1][0], points[1][1])
my_turtle.goto(points[2][0], points[2][1])
my_turtle.goto(points[0][0], points[0][1])
my_turtle.end_fill()
# 삼각형 4등분하기에 필요한 좌표 계산
def get_mid(p1, p2):
return ((p1[0] + p2[0]) / 2, (p1[1] + p2[1]) / 2)
# 시에르핀스키 함수
def sierpinski(points, degree, my_turtle):
colormap = ["blue", "red", "green", "white", "yellow", "violet", "orange"]
draw_triangle(points, colormap[degree], my_turtle)
# time.sleep(1)
# 4등분하기
mid0 = get_mid(points[0], points[1])
mid1 = get_mid(points[1], points[2])
mid2 = get_mid(points[2], points[0])
# 왼쪽 아래 -> 위 -> 오른쪽 아래 순으로 4등분하기를 재귀적으로 반복
if degree > 0:
sierpinski([points[0], mid0, mid2], degree - 1, my_turtle)
sierpinski([mid0, points[1], mid1], degree - 1, my_turtle)
sierpinski([mid2, mid1, points[2]], degree - 1, my_turtle)
# 거북이로 시에르핀스키 삼각형 그리기(degree=4)
my_turtle = turtle.Turtle()
my_win = turtle.Screen()
my_points = [[-180, -150], [0, 150], [180, -150]] # 첫 삼각형 좌표
sierpinski(my_points, 4, my_turtle) # 시에르핀스키 삼각형 그리기
my_win.exitonclick()
사용된 재귀 알고리즘은 가능한한 먼저 왼쪽 아래의 작은 삼각형을 대상으로 4등분하기를 반복한다.
지정된 횟수(degree)만큼 반복하여 더 이상 4등분하기를 할 수 없을 때 위쪽(top)에 위치한
삼각형을 대상으로 4등분하기를 반복하며,
최종적으로 오른쪽 아래의 삼각형을 대상으로 삼는다.