Ctrl+K

서포트 벡터 머신

5. 서포트 벡터 머신#

감사의 글

자료를 공개한 저자 오렐리앙 제롱과 강의자료를 지원한 한빛아카데미에게 진심어린 감사를 전합니다.

소스코드

본문 내용의 일부를 파이썬으로 구현한 내용은 (구글코랩) 서포트 벡터 머신에서 확인할 수 있다.

주요 내용

  • 선형 SVM 분류

  • 비선형 SVM 분류

  • SVM 회귀

  • SVM 이론

슬라이드

본문 내용을 요약한 슬라이드 1부, 슬라이드 2부를 다운로드할 수 있다.

5.1. 선형 SVM 분류#

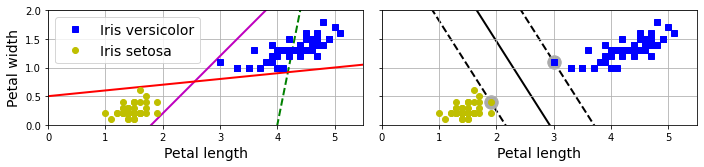
선형 서포트 벡터 머신support vector machine(SVM)은 두 클래스 사이를 최대한으로 경계 도로를 최대한 넓게 잡으려고 시도한다. 이때 두 클래스 사이에 놓을 수 있는 결정 경계 도로의 폭의 마진margin이라 하며, 마진을 최대로 하는 분류가 큰 마진 분류large margin classication이다.

아래 그림은 붓꽃 데이터셋을 대상으로 해서 선형 분류와 큰 마진 분류의 차이점을 보여준다. 선형 분류(왼쪽 그래프)의 경우 두 클래스를 분류하기만 해도 되는 반면에 큰 마진 분류(오른쪽 그래프)의 결정 경계(검은 실선)는 두 클래스와 거리를 최대한 크게 두려는 방향으로 정해진다. 즉, 마진은 가능한 최대로 유지하려 한다. 큰 마진 분류의 결정 경계는 결정 경계 도로의 가장자리에 위치한 서포트 벡터support vector에만 의존하며 다른 데이터와는 전혀 상관 없다. 아래 오른쪽 그래프에서 서포트 벡터는 동그라미로 감싸져 있다.

스케일링과 마진

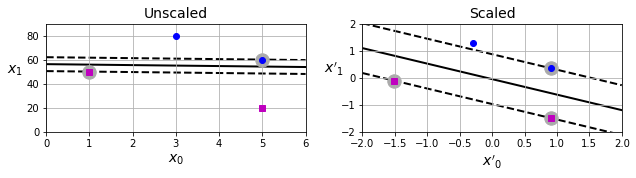
특성의 스케일을 조정하면 결정 경계가 훨씬 좋아진다. 두 특성의 스케일에 차이가 많이 나는 경우(아래 왼쪽 그래프) 보다 표준화된 특성을 사용할 때(아래 오른쪽 그래프) 훨씬 좋은 결정 경계가 찾아진다.

5.1.1. 하드 마진 분류#

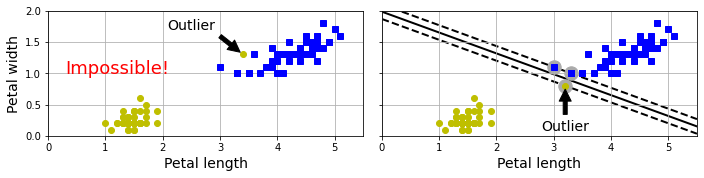
모든 훈련 샘플이 도로 바깥쪽에 올바르게 분류되도록 하는 마진 분류가 하드 마진 분류hard margin classification이다. 하지만 두 클래스가 선형적으로 구분되는 경우에만 적용 가능하다.

또한 이상치에 매우 민감하다. 하나의 이상치가 추가되면 선형 분류가 불가능하거나(아래 왼편 그래프) 일반화가 매우 어려운 분류 모델(아래 오른편 그래프)이 얻어질 수 있다.

5.1.2. 소프트 마진 분류#

소프트 마진 분류soft margin classification는 어느 정도의 마진 오류를 허용하면서 결정 경계 도로의 폭을 최대로 하는 방향으로 유도한다. 마진 오류margin violations는 결정 경계 도로 위에 또는 결정 경계를 넘어 해당 클래스 반대편에 위치하는 샘플을 가리키며 소프트 마진 분류의 서포트 벡터를 구성한다.

예를 들어 꽃잎 길이와 너비 기준으로 붓꽃의 버지니카와 버시컬러 품종을 하드 마진 분류하기는 불가능하며, 아래 그래프에서처럼 어느 정도의 마진 오류를 허용해야 한다.

LinearSVC 클래스

사이킷런의 LinearSVC 클래스는 선형 SVM 분류기를 생성한다.

LinearSVC(C=1, random_state=42)

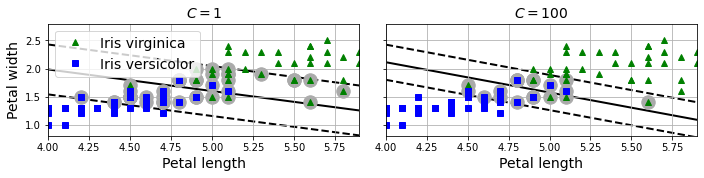
C 는 규제 강조를 지정하는 하이퍼파라미터이며 클 수록 적은 규제를 의미한다. C 가 너무 작으면(아래 왼편 그래프) 마진 오류를 너무 많이 허용하는 과소 적합이 발생하며, C 를 키우면(아래 오른편 그래프) 결정 경계 도로 폭이 좁아진다. 여기서는 C=100 이 일반화 성능이 좋은 모델을 유도하는 것으로 보인다. 또한 C=float("inf")로 지정하면 하드 마진 분류 모델이 된다.

선형 SVM 지원 모델

LinearSVC 모델은 대용량 훈련 데이터셋을 이용해서도 빠르게 학습한다. 이외에 SVC 모델과 SGDClassifier 모델도 선형 SVM 분류 모델로 활용될 수 있다.

  • SVC 클래스 활용

    SVC(kernel="linear", C=1)

  • SGDClassifier 클래스 활용

    SGDClassifier(loss="hinge", alpha=1/(m*C))

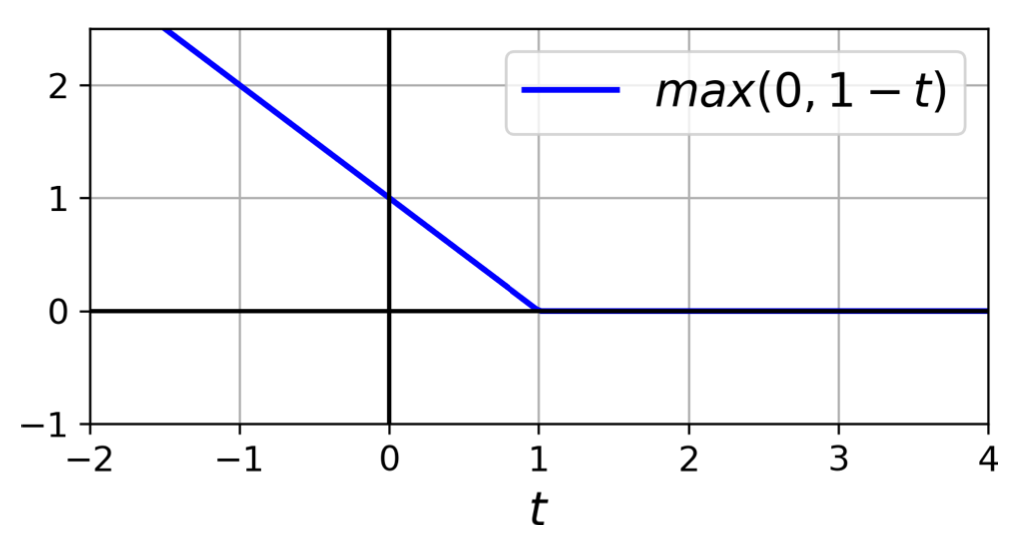
  • hinge 손실 함수: 어긋난 예측 정도에 비례하여 손실값이 선형적으로 커짐.

:::

5.2. 비선형 SVM 분류#

선형적으로 구분되지 못하는 데이터셋을 대상으로 분류 모델을 훈련시키는 두 가지 방식을 소개한다.

  • 방식 1: 특성 추가 + 선형 SVC

    • 다항 특성 활용: 다항 특성을 추가한 후 선형 SVC 적용

    • 유사도 특성 활용: 유사도 특성을 추가한 후 선형 SVC 적용

  • 방식 2: SVC + 커널 트릭

    • 커널 트릭: 새로운 특성을 실제로 추가하지 않으면서 동일한 결과를 유도하는 방식

    • 예제 1: 다항 커널

    • 예제 2: 가우스 RBF(방사 기저 함수) 커널

다항 특성 추가 + 선형 SVC

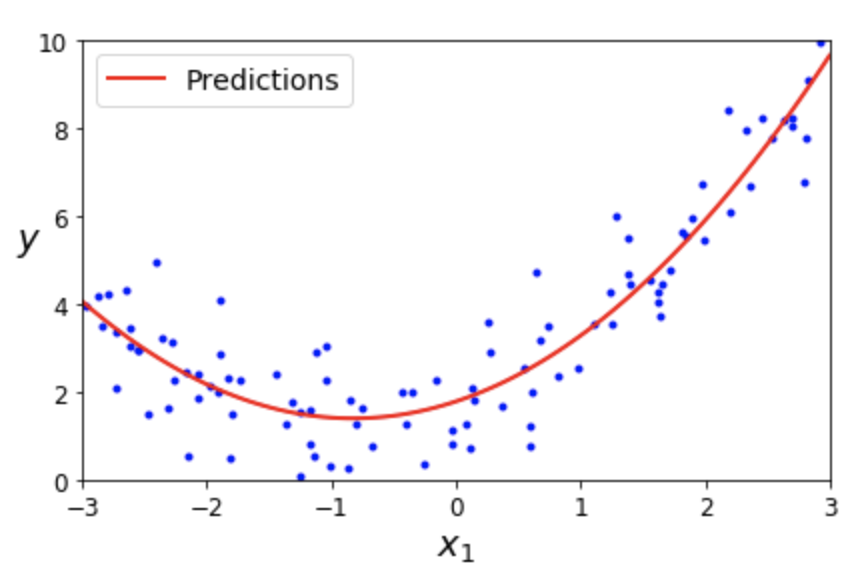
4.3절에서 설명한 다항 회귀 기법에서 다항 특성을 추가한 후에 선형 회귀를 적용한 방식과 동일하다. 아래 그래프는 특성 \(x_1\) 하나만 갖는 데이터셋에 특성 \(x_1^2\)을 추가한 후 선형 회귀 모델을 적용한 결과를 보여준다.

\[\hat y = \theta_0 + \theta_1\, x_1 + \theta_2\, x_1^{2}\]

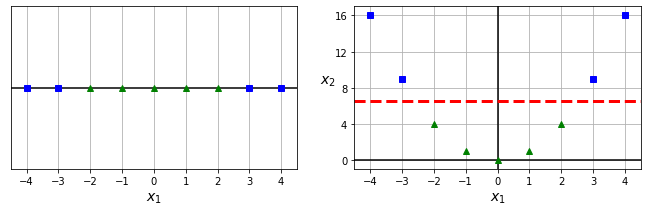
동일한 아이디어를 특성 \(x_1\) 하나만 갖는 데이터셋(아래 왼편 그래프)에 적용하면 비선형 SVM 모델(아래 오른편 그래프)을 얻게 된다.

2차 다항 특성 추가 후 선형 SVM 분류 모델 훈련

아래 사진은 두 개의 특성을 갖는 데이터셋에 2차 다항 특성을 추가한 후에 선형 SVM 분류 모델을 적용하는 과정을 보여준다.

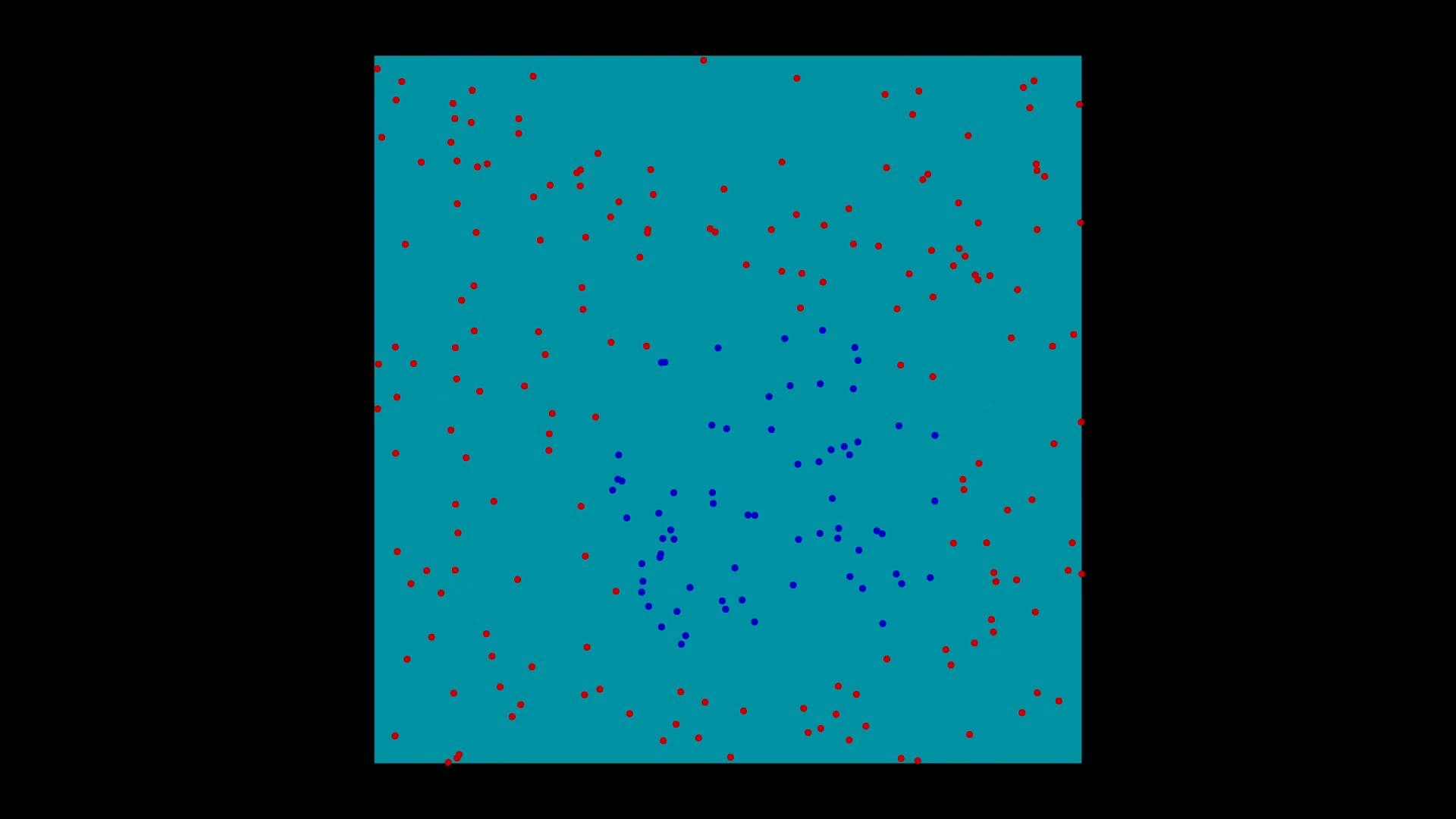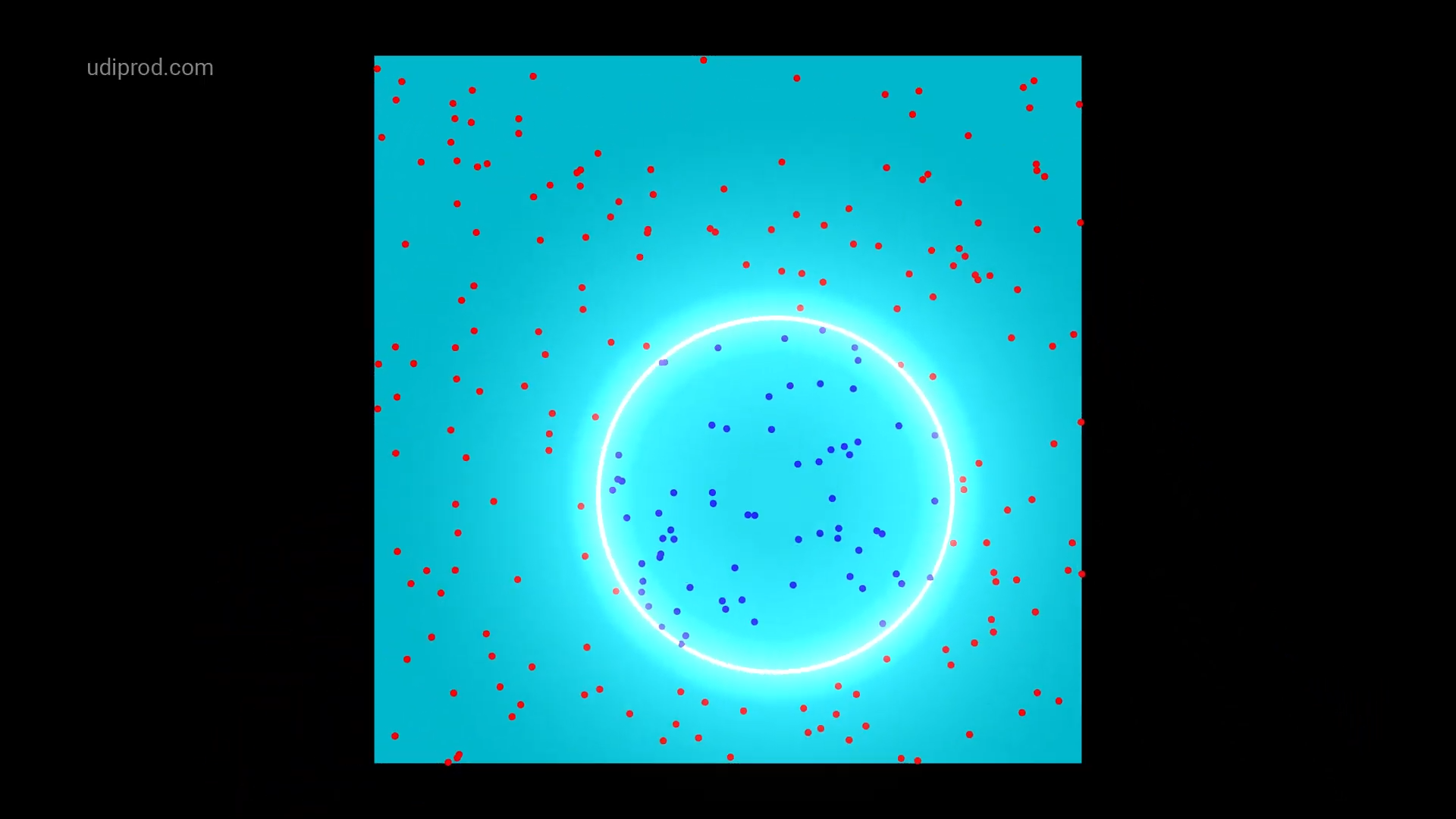<그림 출처: SVM with polynomial kernel visualization(유튜브)>

참고로 3차원 상에서의 선형 방정식의 그래프는 평면으로 그려진다. 예를 들어, 방정식 \(3x + y - 5z + 25 = 0\) 의 그래프는 아래와 같다.

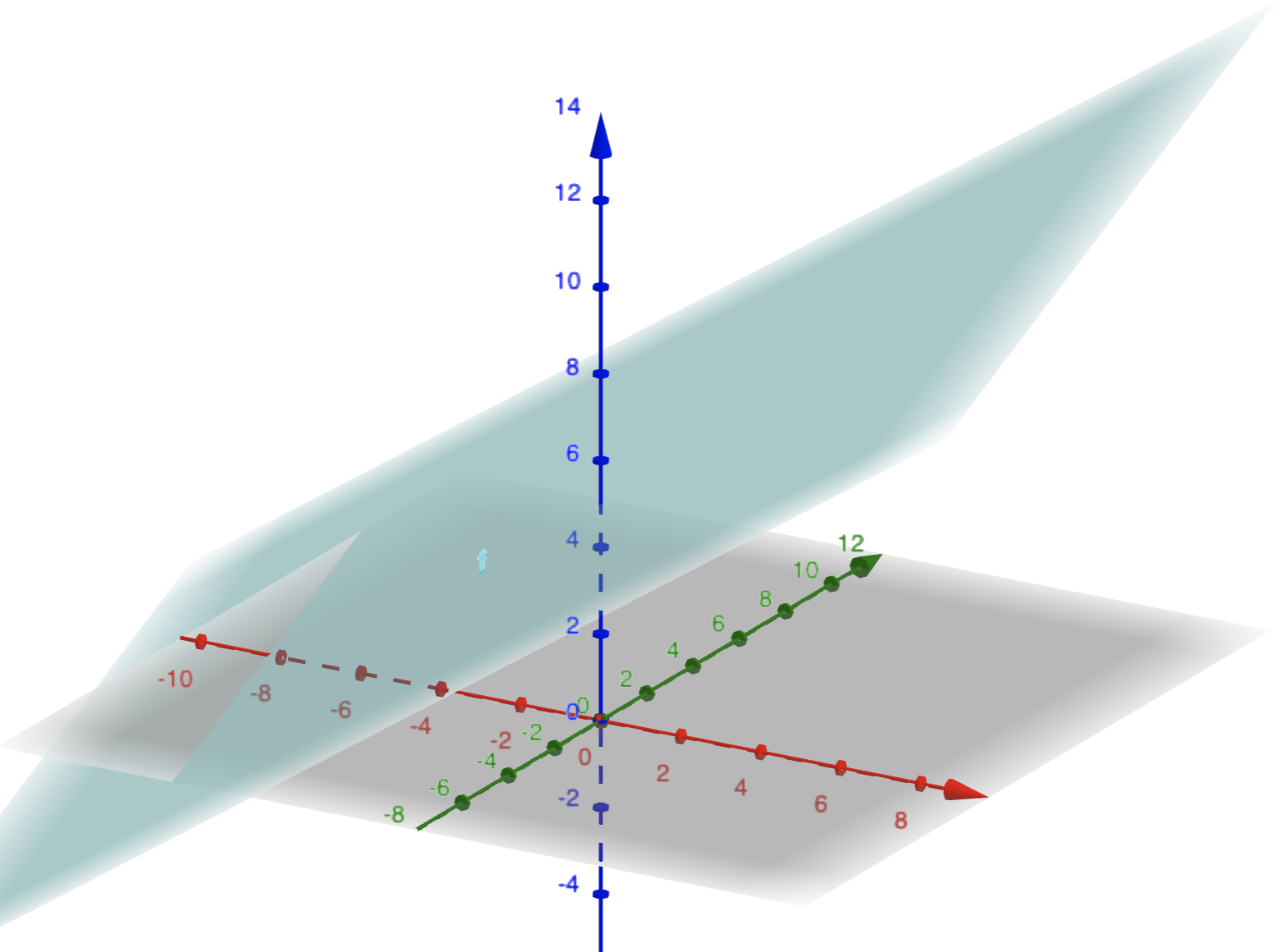
<그림 출처: 지오지브라(GeoGebra)>

Example 5.1 (초승달 데이터셋moons dataset)

초승달 데이터셋은 마주보는 두 개의 초승달 모양의 클래스로 구분되는 데이터셋을 가리킨다.

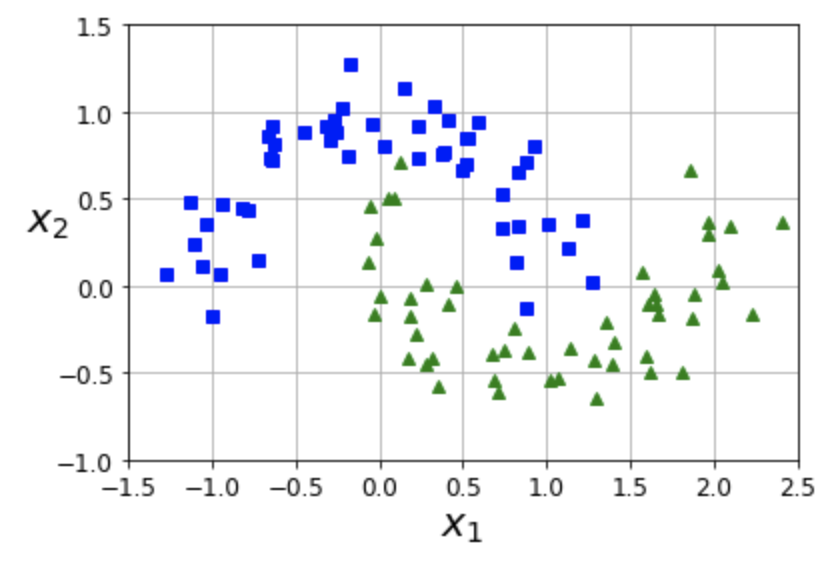
위 데이터셋에 선형 SVM 분류 모데를 적용하기 위해 먼저 3차 항에 해당하는 특성을 추가하면 비선형 분류 모델을 얻게 된다.

# 3차 항까지 추가
polynomial_svm_clf = make_pipeline(
    PolynomialFeatures(degree=3),
    StandardScaler(),
    LinearSVC(C=10, max_iter=10_000, random_state=42)
)

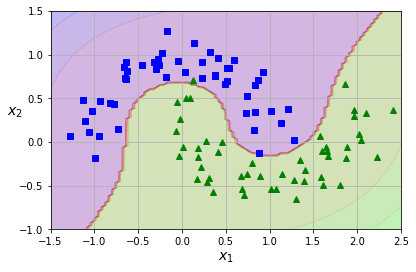
5.2.1. 다항 커널#

다항 특성을 추가하는 기법은 그만큼 비용을 지불해야 한다. 특히 축가해야 하는 특성이 많다면 시간과 메모리 사용 비용이 엄청날 수 있다. 반면에 커널 트릭kernel trick을 사용하면 다항 특성을 실제로는 추가하지 않지만 추가한 경우와 동일한 결과를 만들어 낼 수 있다. 다만 이것은 SVM을 적용하는 경우에만 해당한다. 이와 달리 다항 특성을 추가하는 기법은 어떤 모델과도 함께 사용될 수 있다.

아래 두 그래프는 커널 기법을 사용하는 SVC 모델을 초승달 데이터셋에 대해 훈련시킨 결과를 보여준다.

poly_kernel_svm_clf = make_pipeline(StandardScaler(),
                                    SVC(kernel="poly", degree=3, coef0=1, C=5))

위 코드는 3차 다항 커널을 적용한 모델이며 아래 왼편 그래프와 같은 분류 모델을 학습한다. 반면에 아래 오른편 그래프는 10차 다항 커널을 적용한 모델이다. coef0 하이퍼파라미터는 고차항의 중요도를 지정하며, 아래 이미지에서는 \(r\) 이 동일한 하이퍼파라미터를 가리킨다.

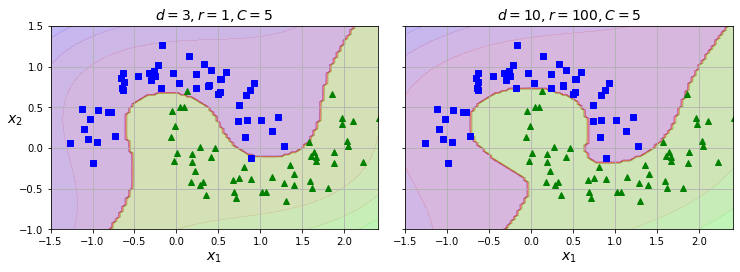
하이퍼파라미터 이해의 중요성

다항 커널 모델이 과대 적합이면 차수를 줄여야 하고, 과소 적합이면 차수를 늘려야 한다. 적절한 하이퍼파라미터는 그리드 탐색 등을 이용하여 찾으면 되지만, 그럼에도 불구하고 하이퍼파라미터의 의미를 잘 알고 있으면 탐색 구간을 줄일 수 있다.

5.2.2. 유사도 특성#

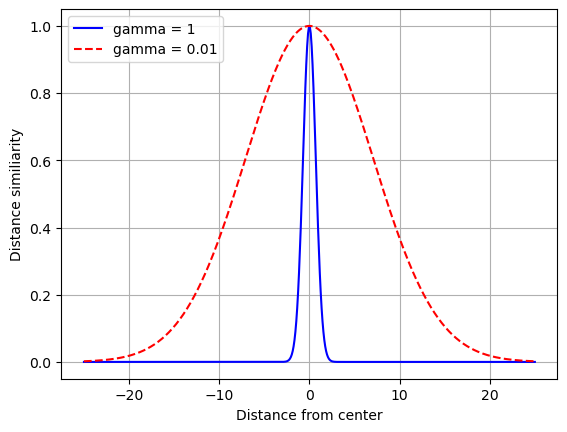
가우스 방사 기저 함수를 이용한 유사도 특성similarity feature은 랜드마크landmark로 지정된 특정 샘플과 각 샘플이 얼마나 유사한가를 계산한다. 가우스 방사 기저 함수Gaussian radial basis function(Gaussian RBF)의 정의는 다음과 같다. 특정 지점을 가리키는 랜드마크landmark인 \(\mathbf{m}\)으로부터 조금만 멀어져도 함숫값이 급격히 작아진다.

\[ \phi(\mathbf{x},\mathbf{m}) = \exp \left( -\gamma \|\mathbf{x} - \mathbf{m} \|^2 \right) \]

하이퍼파라미터인 감마(\(\gamma\), gamma)는 데이터 샘플이 랜드마크로부터 멀어질 때 가우스 RBF 함수의 반환값이 얼마나 빠르게 0에 수렴하도록 하는가를 결정한다. 감마 값이 클 수록 랜드마크로부터 조금만 멀어져도 보다 빠르게 0에 수렴한다. 따라서 가우스 RBF 함수의 그래프가 보다 좁은 종 모양을 띤다.

예를 들어 아래 그래프는 감마가 1일 때와 0.01 때의 차이를 명확하게 보여준다. 즉 랜드마크인 \(\mathbf{m}=\) 0으로부터 거리가 멀어질 때 감마가 1이면 매우 급격하게 함숫값이 0으로 줄어든다. 즉, 랜드마크로부터 조금만 멀어저도 유사도가 매우 빠르게 약해진다.

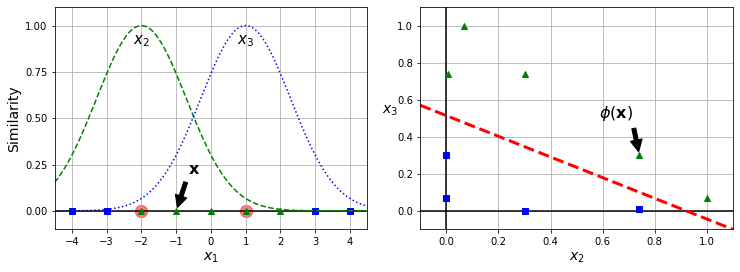
유사도 특성 추가와 선형 SVC

아래 왼쪽 그래프는 -2와 1을 두 개의 랜드마크로 지정한 다음에 가우스 RBF 함수로 계산한 유사도 특성값을 보여준다. \(x_2\)와 \(x_3\)는 각각 -2와 1를 랜드마크로 사용한 유사도이며, 오른쪽 그래프는 이들을 이용하면 선형 분류가 가능해짐을 보여준다.

5.2.3. 가우스 RBF 커널#

일반적으로 모든 훈련 샘플을 랜드마크로 지정한 후에 각 랜드마크에 대한 유사도를 새로운 특성으로 추가하는 방식이 사용된다. 그런데 그러면 훈련셋의 크기 만큼의 특성이 새로 추가된다. 따라서 훈련 세트가 매우 크다면 새로운 특성을 계산하는 데에 아주 많은 시간과 비용이 들게 된다.

다행히도 SVM 모델을 이용하면 유사도 특성을 실제로는 추가 하지 않으면서 추가한 효과를 내는 결과를 얻도록 훈련을 유도할 수 있다.

rbf_kernel_svm_clf = make_pipeline(StandardScaler(),
                                   SVC(kernel="rbf", gamma=5, C=0.001))

아래 네 개의 그래프는 초승달 데이터셋에 가우스 RBF 커널을 다양한 gamma 와 C 규제 옵션과 함께 적용한 결과를 보여준다.

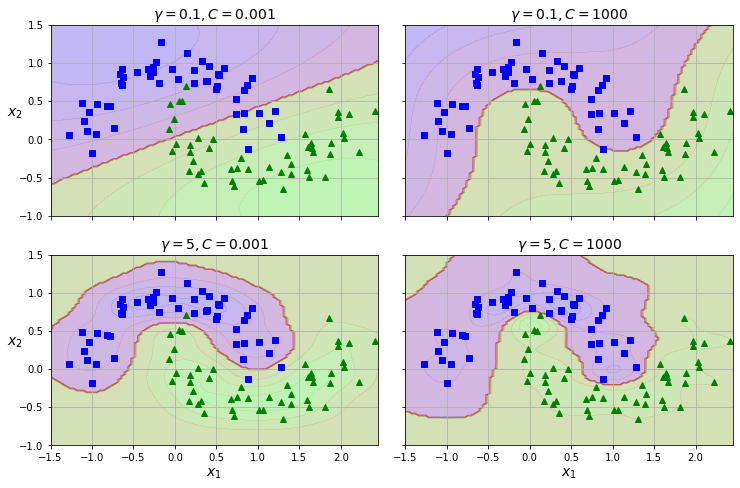
위 그래프에 따르면 gamma 또한 나름 규제 역할을 수행함을 볼 수 있다. gamma 값을 키우면 각 샘플의 영향력이 보다 작은 영역으로 제한되어 경계 구분선이 보다 좁고 복잡하게 움직인다. 반면에 gamma 값을 줄이면 각 샘플의 영향력이 보다 넓은 영역까지 전해지게 되어 경계 구분선이 보다 부드러워진다.

SVC 클래스의 의 kernel 기본값은 "rbf"이며 대부분의 경우 이 커널이 잘 맞는다. 하지만 교차 검증, 그리드 탐색 등을 이용하여 적절한 커널을 찾아볼 수 있다. 특히 훈련 세트에 특화된 커널이 알려져 있다면 해당 커널을 먼저 사용해봐야 한다.

5.2.4. SVM 계산 복잡도#

SGDClassifier 클래스는 확률적 경사하강법을 적용하기에 온라인 학습에 활용될 수 있다. 아래 표에서 ‘외부 메모리 학습’out-of-core learning 항목이 온라인 학습 지원 여부를 표시한다. 또한 LinearSVC 클래스와 거의 동일한 결과를 내도록 하이퍼파라미터를 조정할 수 있다. 하지만 LinearSVC 클래스는 배치학습과 다른 옵티마이저 알고리즘을 사용한다.

클래스

시간 복잡도(m 샘플 수, n 특성 수)

외부 메모리 학습

스케일 조정

커널

다중 클래스 분류

LinearSVC

\(O(m \times n)\)

미지원

필요

미지원

OvR

SVC

\(O(m^2 \times n) \sim O(m^3 \times n)\)

미지원

필요

지원

OvR

SGDClassifier

\(O(m \times n)\)

지원

필요

미지원

OvR

5.3. SVM 회귀#

SVM 아이디어를 조금 다르게 적용하면 회귀 모델이 생성된다.

  • 목표: 마진 오류 발생 정도를 조절(C 이용)하면서 지정된 폭의 도로 안에 가능한 많은 샘플 포함하기

  • 마진 오류: 도로 밖에 위치한 샘플

  • 결정 경계 도로의 폭: epsilon 하이퍼파라미터로 지정

보다 자세한 설명은 SVM 회귀 이해하기를 참고한다.

참고로 SVM 분류 모델의 특징은 다음과 같다.

  • 목표: 마진 오류 발생 정도를 조절(C 이용)하면서 두 클래스 사이의 도로폭을 최대한 넓게 하기

  • 마진 오류: 도로 위 또는 자신의 클래스 반대편에 위치한 샘플

선형 SVM 회귀

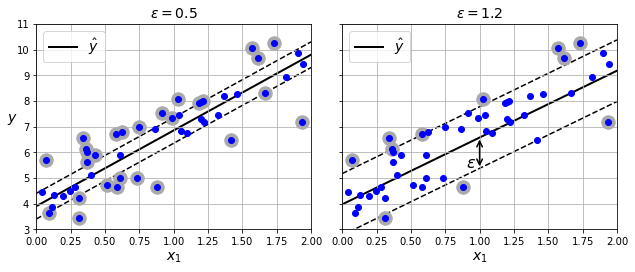
아래 그래프는 LinearSVR 클래스를 이용한 결과를 보여준다. epsilon(\(\varepsilon\))이 작을 수록(왼쪽 그래프) 도로폭이 좁아진다. 따라서 보다 많은 샘플을 도로에 포함시키기 위해 굴곡이 심해지며 결과적으로 보다 많은 서포트 벡터가 지정된다. 반면에 도로 위(마진)에 포함되는 샘플를 추가해도 예측에 영향 주지 않는다.

svm_reg = make_pipeline(StandardScaler(),
                        LinearSVR(epsilon=0.5, random_state=42))

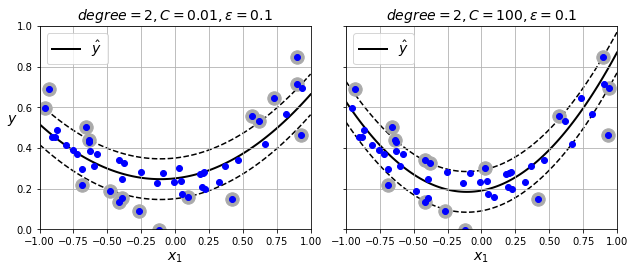
비선형 SVM 회귀

SVC에 커널 트릭을 적용하는 아이디어를 동일하게 활용하여 비선형 회귀 모델을 구현한다. 아래 그래프는 SVR 클래스에 2차 다항 커널을 적용한 결과를 보여준다.

# SVR + 다항 커널
svm_poly_reg2 = make_pipeline(StandardScaler(),
                             SVR(kernel="poly", degree=2, C=100))

C 하이퍼파라미터의 의미는 SVC 모델의 경우와 동일하다. 즉, C 는 클 수록 적은 규제를 가하고 epsilon은 도로폭을 결정한다. C=100 인 경우(오른쪽 그래프)가 C=0.01 인 경우(왼쪽 그래프) 보다 마진 오류가 적음을 볼 수 있다.

회귀 모델 시간 복잡도

LinearSVR 은 LinearSVC 의 회귀 버전이며 시간 복잡도 또한 비슷하다. 또한 훈련 세트의 크기에 비례해서 선형적으로 증가한다. SVR은 SVC의 회귀 버전이며, 훈련 세트가 커지면 매우 느려지는 점 또한 동일하다.

5.4. SVM 이론#

선형 SVM 분류의 작동 원리를 설명한다.

결정 함수와 예측

아래 결정 함숫값을 이용하여 클래스를 지정한다.

\[ h(\mathbf x) = \mathbf w^T \mathbf x + b = w_1 x_1 + \cdots + w_n x_n + b \]

결정 함숫값이 양수이면 양성, 음수이면 음성으로 분류한다.

\[\begin{split} \hat y = \begin{cases} 0 & \text{if } h(\mathbf x) < 0\\ 1 & \text{if } h(\mathbf x) \ge 0 \end{cases} \end{split}\]

결정 경계

결정 경계는 결정 함수의 값이 0인 점들의 집합이다.

\[\{\mathbf x \mid h(\mathbf x)=0 \}\]

결정 경계 도로의 가장자리는 결정 함수의 값이 1 또는 -1인 샘플들의 집합이다.

\[\{\mathbf{x} \mid h(\mathbf x)= \pm 1 \}\]

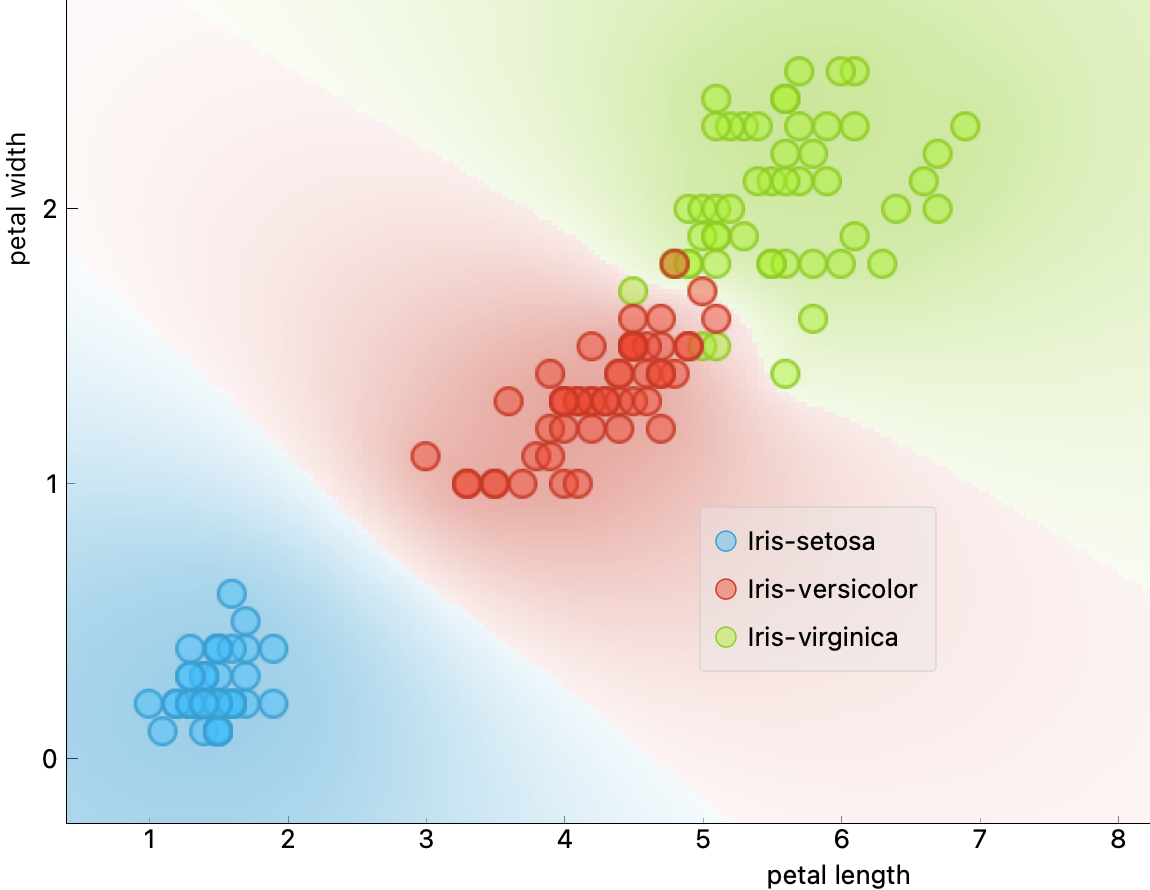
Example 5.2 (붓꽃 분류)

꽃잎 길이와 너비를 기준으로 버지니카(Iris-Virginica, 초록 삼각형) 품종 여부를 판단하는 이진 분류 모델의 결정 함수는 다음과 같다.

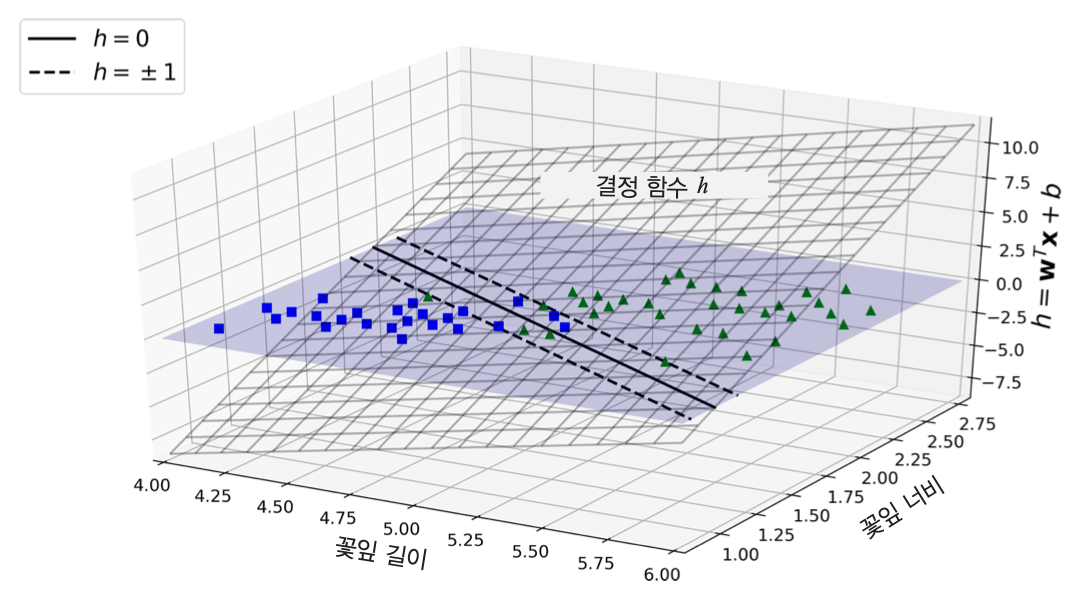
결정 함수의 기울기

결정 경계 하이퍼플레인(결정 함수의 그래프)의 기울기가 작을 수록 도로 경계 폭이 커진다. 그리고 결정 경계면 기울기는 \(\| \mathbf w \|\)(\(\mathbf w\)의 \(l_2\)-노름)에 비례한다. 따라서 결정 경계 도로의 폭을 크게 하기 위해 \(\| \mathbf w \|\)를 최소화해야 한다.

목적 함수

결정 경계면의 기울기 \(\| \mathbf w \|\)를 최소화하는 것과 아래 식을 최소화하는 것이 동일한 결과를 낳는다. 따라서 아래 식을 목적 함수로 지정한다.

\[\frac 1 2 \| \mathbf w \|^2 = \frac 1 2 \mathbf w^T \mathbf w\]

이유는 함수의 미분가능성 때문에 수학적으로 보다 다루기 쉽기 때문이다.

하드 마진 선형 SVM 분류기의 목표

아래 조건식을 만족시키면서

\[t^{(i)} (\mathbf w^T \mathbf x^{(i)} + b) \ge 1\]

다음 수식을 최소화하는 \(\mathbf{w}\), \(b\) 를 찾아야 한다.

\[\frac 1 2 \mathbf w^T \mathbf w\]

단, \(t^{(i)}\)는 \(i\) 번째 샘플의 클래스(양성/음성)를 가리킨다.

\[\begin{split} t^{(i)} = \begin{cases} -1 & \text{$x^{(i)}$가 음성인 경우} \\ 1 & \text{$x^{(i)}$가 양성인 경우} \end{cases} \end{split}\]

소프트 마진 선형 SVM 분류기의 목표

아래 조건식 \((*)\) 을 만족시키면서

\[t^{(i)} (\mathbf w^T \mathbf x^{(i)} + b) \ge 1 - \zeta^{(i)}\tag{$*$}\]

다음 수식 \((\dagger)\) 을 최소화하는 \(\mathbf{w}\), \(b\), \(\zeta^{(i)}\) 를 찾아야 한다.

\[\frac 1 2 \mathbf w^T \mathbf w + C \sum_{i=0}^{m-1} \zeta^{(i)}\tag{$\dagger$}\]

위 식에서 \(\zeta^{(i)}\ge 0\)는 슬랙 변수 변수라 불리며 \(i\) 번째 샘플의 마진 오류 허용 정도를 나타낸다. \(\zeta\)는 그리스어 알파벳이며 체타zeta라고 발음한다.

슬랙 변수

슬랙 변수가 샘플마다 다름에 주의하라. 만약에 샘플과 무관한 하나의 \(\zeta\) 를 사용하면 하드 마진 분류와 기본적으로 동일한 문제가 된다.

조건식의 의미

조건식 \((*)\) 의 의미는 다음과 같다.

  • \(\mathbf x^{(i)}\) 가 양성, 즉 \(t^{(i)} = 1\) 인 경우: 아래 식이 성립해야 한다. 즉, \(1-\zeta^{(i)}\) 만큼의 오류를 허용하면서 가능한한 양성으로 예측해야 한다.

    \[\mathbf w^T \mathbf x^{(i)} + b \ge 1 - \zeta^{(i)}\]

  • \(\mathbf x^{(i)}\)가 음성, 즉 \(t^{(i)} = -1\) 인 경우: 아래 식이 성립해야 한다. 즉, \(1-\zeta^{(i)}\) 만큼의 오류를 허용하면서 가능한한 음성으로 예측해야 한다.

    \[\mathbf w^T \mathbf x^{(i)} + b \le -1 + \zeta^{(i)}\]

\(C\) 와 마진 폭의 관계

\(C\) 가 커지면 수식 \((\dagger)\) 의 값을 줄이기 위해 \(\zeta^{(i)}\) 가 작아져야 하며, 따라서 \(\mathbf w^T \mathbf w\) 값에 여유가 생긴다. 이는 조건식 \((*)\) 를 만족시키기 위해 결정경계 하이퍼플레인의 기울기, 즉 \(\|\mathbf{w}\|\)의 값을 키울 여력이 생기게 됨을 의미한다. 결국 \(\|\mathbf{w}\|\) 가 좀 더 커지도록 훈련되며 이는 결정경계 하이퍼플레인의 기울기가 커지게되어 결정 경계 도로의 폭이 좁아지게 된다.

선형 분류가 가능하다면, 즉 하드 마진 분류가 가능하다면 \(\zeta^{(i)}\) 는 자연스럽게 0으로 또는 매우 작은 값으로 유도되어, 결국 \(\|\mathbf w\|\) 가 아래 조선식을 만족시키면서 최소값을 갖도록, 즉 결정 경계 하이퍼플레인의 기울기가 최대한 작아지도록 유도된다.

\[t^{(i)} (\mathbf w^T \mathbf x^{(i)} + b) \ge 1\]

참고로 \(C\) 를 무한으로 두는 경우에도 동일하게 작동한다. 즉, 하드 마진 분류가 이루어진다.

쌍대 문제

어떤 문제의 쌍대 문제dual problem는 주어진 문제와 동일한 답을 갖는 문제이며, 주어진 원래의 문제를 원 문제primal problem라 부른다

여기서는 앞서 선형 SVM 분류기의 목표로 설명된 문제가 원 문제이며, 이에 대응하는 쌍대 문제가 알려져 있지만, 여기서는 자세히 다루지 않으며 대신 핸즈온 머신러닝의 5장을 참고할 것을 추천한다.

여기서는 다만 SVC와 SVR 의 커널 기법이 바로 이 쌍대 문제에 적용된다는 점과 LinearSVC 과 LinearSVR 은 dual 하이퍼파라미터를 이용하여 쌍대 문제를 이용하여 모델을 훈련시킬지 여부를 지정할 수 있다는 정도만 언급한다. dual=True 가 기본값이지만 훈련 샘플의 수가 특성 수보다 큰 경우 dual=False 로 지정하여 원 문제를 이용하는 것을 추천한다.

5.5. 연습문제#

참고: (실습) 서포트 벡터 머신

Contents