4. 모델 훈련#
감사의 글
자료를 공개한 저자 오렐리앙 제롱과 강의자료를 지원한 한빛아카데미에게 진심어린 감사를 전합니다.
소스코드
본문에 소개된 코드는 (구글코랩) 모델 훈련에서 직접 실행할 수 있다.
주요 내용
선형 회귀
경사하강법
다항 회귀
모델 규제
로지스틱 회귀
슬라이드
본문 내용을 요약한 슬라이드 1부, 슬라이드 2부 다운로드할 수 있다.
4.1. 선형 회귀#
지금까지 살펴 본 두 개의 선형 회귀 모델을 이용하여 머신러닝 모델의 기능과 훈련 과정의 이해에 중요한 기초 개념을 살펴 본다. 선형 회귀 모델을 예제로 사용하는 이유는 크게 두 가지다.
첫째, 선형 회귀 모델의 훈련 과정이 매우 단순하여 머신러닝의 기초 개념을 설명하는 데에 매우 유용하다.
둘째, 딥러닝 심층 신경망 모델 등 대다수의 머신러닝 모델이 훈련 과정에서 선형 회귀 모델의 훈련 방식을 활용하면서 보다 복잡한 문제들을 해결한다.
4.1.1. 머신러닝 모델이란?#
먼저 앞서 살펴 본 두 개의 선형 회귀 모델이 예측값을 계산하는 방식을 확인한다.
예제: 1인당 GDP와 삶의 만족도
1.5절에서 1인당 GDP와 삶의 만족도 사이의 관계를 다음 1차 방정식 함수로 표현할 수 있었다.
위 함수는 1인당 GDP가 주어지면 삶의 만족도를 예측한다. 이를 보다 수학적으로 표현하면 다음과 같다.
위 식에서 \(x_1\)은 1인당 GDP를 가리키는 특성값이고, \(\hat y\)는 예측된 삶의 만족도다.
예제: 캘리포니아 주택 가격 예측
2장에서 다룬 캘리포니아 주택 가격 예측 선형 회귀 모델은 24개의 입력 특성을 다룬다. 따라서 아래 모양의 아래 함수를 이용하여 예측값을 계산한다.
\(\hat y\): 예측된 주택 중위 가격
\(x_i\): 구역의 \(i\) 번째 특성값(위도, 경도, 중간소득, 가구당 인원 등)
\(\theta_0\): 편향
\(\theta_i\): \(i\) 번째 특성에 대한 가중치. 단, \(1 \le i \le 24\).
선형 회귀 예측값
위 두 개의 예제에서 설명한 선형 회귀 모델이 예측값을 생성할 때 사용하는 선형 함수를 일반화하면 다음과 같다.
먼저 훈련셋에 포함된 샘플이 \(n\) 개의 특성 \(x_1\), \(x_2\), …, \(x_n\)을 갖는다고 가정한다. 그러면 선형 회귀 모델은 아래 식을 이용하여 예측값을 계산한다. \(\theta_0\)와 1을 곱해주는 이유는 다른 항과의 형식을 맞추기 위함이다.
아래 사진은 위 식을 시각화한다.
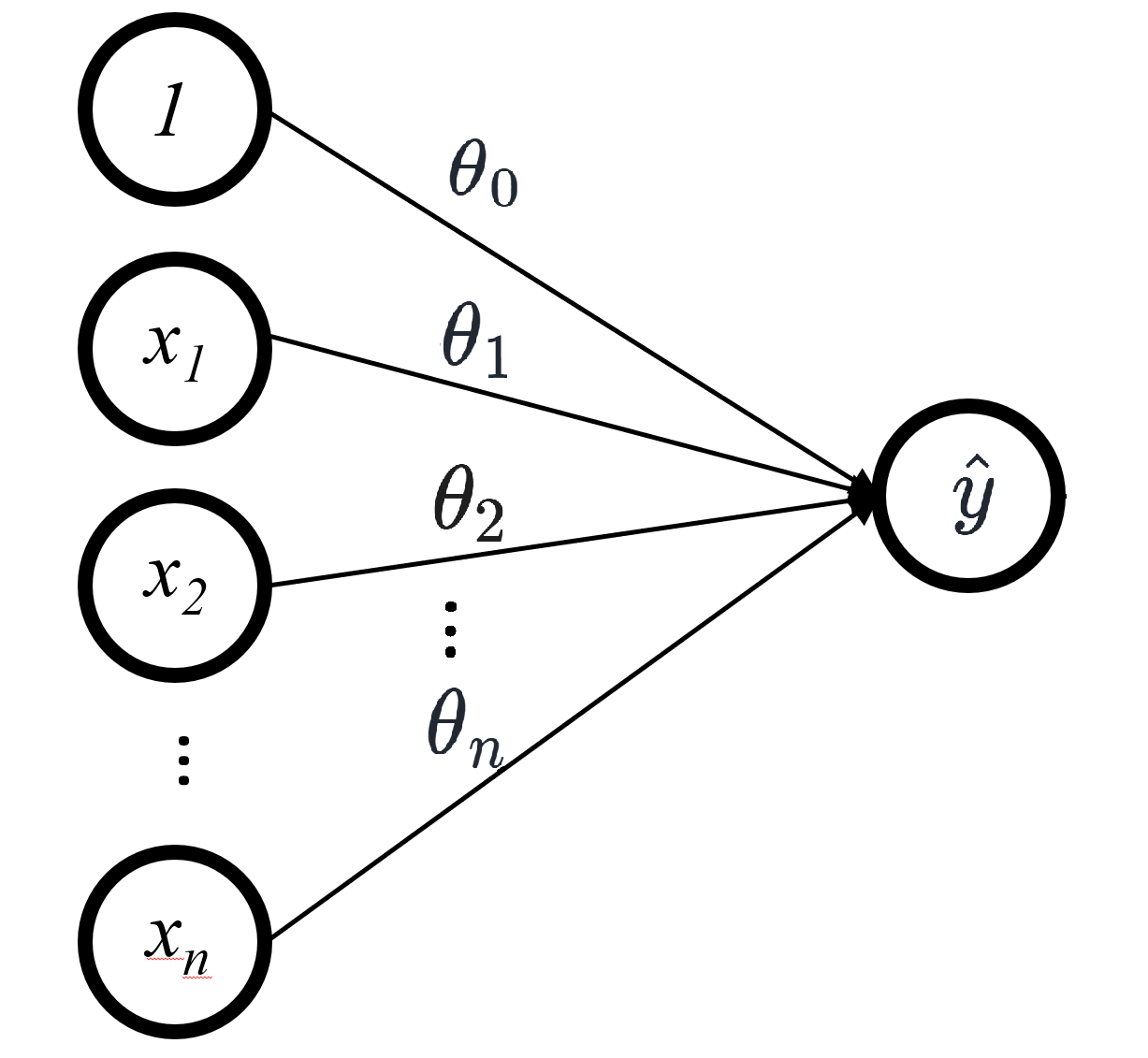
선형 회귀 모델 훈련
입력값과 타깃 사이의 숨은 관계를 알아내는 일이 바로 머신러닝 모델을 훈련시키는 주요 목표다. 예를 들어 선형 회귀 모델은 입력값과 예측값 사이의 관계를 앞서 설명한 대로 입력값의 특성과 \(\theta_i\)의 선형 조합으로 추정한다. 선형 회귀 모델을 훈련시킬 때 \(\theta_i\)를 처음에는 무작위로 선택해서 점차 보다 좋은 값으로 업데이트하면서 최적의 \(\theta_i\)를 찾아가는데, 이때 일반적으로 경사하강법을 적용한다.
모든 머신러닝 모델은 각자 고유의 방식으로 예측값을 계산하며, 일반적으로 학습된 파라미터를 이용하여 예측값을 계산한다. 파라미터 학습은 일반적으로 경사하강법을 이용하며 선형 회귀 모델의 훈련 방식과 예측값 계산 방식이 기초를 제공한다.
파라미터, 편향, 가중치
선형 회귀 모델이 입력값에 대한 예측값을 계산할 때 사용하는 \(\theta_0\), \(\theta_1\), …, \(\theta_{n}\)은 모델이 훈련을 통해 학습한 파라미터parameter다. 파라미터 중에 \(\theta_0\)은 편향bias, 나머지 파라미터는 가중치weight라 부른다.
4.1.2. 행렬 연산 표기법#
지금까지 설명한 선형 회귀 모델의 예측값은 하나의 입력값에 대해서만 계산되는 방식이다. 그런데 머신러닝 모델은 임의의 개수의 입력값에 대해 동시에 예측값을 계산할 수 있다.
사이킷런의 모든 머신러닝 모델은 입력값으로 2차원 어레이를 요구한다.
예를 들어 4개의 특성을 갖는 입력값에 대해 훈련된 모델은 입력값으로 임의의 양의 정수 m에 대해
(m, 4) 모양의 데이터프레임 또는 2차원 어레이를 입력값으로 받아 예측값을 계산한다.
4개의 특성을 사용하는 훈련셋으로 훈련된 LinearRegression 모델은 훈련중에 또는 실전에서
아래 (3, 4) 모양의 2차원 어레이를 입력값으로 받으면 3개의 예측값을 계산한다.
X = array([[0.89, 0.37, 0.39, 0.97],
[0.95, 0.04, 0.24, 0.02],
[0.57, 2.91, 1.25, 0.39]])
(3, 4) 모양의 어레이를 일반적인 형태를 다음과 같이 표현할 수 있다.
단, \(x_j^{(i)}\)는 \(i\)-번째 샘플의 \(j\)-번째 특성값을 가리킨다.
즉, \(i\)는 1부터 3까지, \(j\)는 1부터 4까지 움직인다.
그러면 3개의 예측값을 계산하기 위해 선형 회귀 모델은 내부에서 아래 형식의 행렬곱셈을 수행한다. 첫째 열에 추가된 1은 편향에 곱해지는 값을 맞추기 위함이다.
따라서 앞서 언급된 (3, 4) 모양의 2차원 어레이 X에 대한 예측값은 다음과 같이 계산된다.
4.1.3. 머신러닝 모델 훈련의 목표#
머신러닝 모델의 훈련은 타깃에 최대한 가까운 예측값 계산을 목표로 한다. 한마디로 말해 모델의 예측 성능을 최대한 높혀야 한다. 모델 훈련중에는 모델의 성능을 일반적으로 모델의 비용 함수를 이용하여 계산한다.
비용 함수
비용 함수cost function는 모델의 성능이 얼마나 나쁜가를 계산한다. 비용 함수가 계산하는 값이 작을 수록 해당 모델의 성능이 좋은 것이다.
비용 함수와 손실 함수
비용 함수는 손실 함수loss function, 비용 함수에 의해 계산된 값은 손실값loss이라 부르기도 한다. 사람에 따라 두 함수의 기능을 구분하기도 하지만 여기서는 동일한 함수로 취급한다.
MSE: 회귀 모델의 비용 함수
비용 함수는 모델 종류와 목표에 따라 다르게 정의되지만 회귀 모델의 경우 일반적으로 평균 제곱 오차mean squared error(MSE)를 비용 함수로 사용한다.
위 수식에서 포함된 기호들의 의미는 다음과 같다.
기호 |
의미 |
|---|---|
\(\mathbf{x}^{(i)}\) |
\(i\) 번째 샘플. 단 0번 인덱스에 1이 추가됨. |
\(y^{(i)}\) |
\(i\) 번째 샘플에 대한 타깃 |
\(\mathbf{\theta}\) |
파라미터(편향과 가중치)로 구성된 1차원 어레이 |
\(m\) |
훈련셋 크기 또는 배치 크기 |
또한 \(\mathbf{x}^{(i)}\, \mathbf{\theta}\) 는 \(i\)-번째 샘플에 대한 예측값 \(\hat y^{(i)}\)를 가리킨다. 이때 \(i\)는 \(1\)부터 \(m\)까지 움직인다.
모델 훈련의 최종 목표
훈련셋이 주어졌을 때 \(\mathrm{MSE}(\mathbf{\theta})\)가 최소가 되도록 하는 \(\mathbf{\theta}\)를 찾아야 한다. 선형 회귀의 경우 모델에 따라 다음 두 가지 방식 중 하나를 이용하여 해결한다.
방식 1: 정규방정식 또는 특이값 분해(SVD)
방식 2: 경사하강법
정규 방정식은 LinearRegression 등 선형 회귀를 활용하는 극히 일부 모델에서, 그것도 훈련셋의 크기와
입력 특성수 모두 작을 때만 활용된다.
반면에 경사하강법은 딥러닝 모델에서도 기본으로 활용되는 훈련 기법이다.
이런 의미에서 정규 방정식은 여기서는 다루지 않는다.
4.2. 경사하강법#
경사하강법을 이해하려면 먼저 아래 개념들을 충분히 숙지해야 한다.
하이퍼파라미터hyperparameter
훈련시킬 모델을 지정할 때 사용되는 설정 옵션, 즉 해당 클래스의 객체를 생성할 때 클래스의 생성자 함수에 전달되는 인자들을 가리킨다. 대표적으로 학습률, 에포크, 허용 오차, 배치 크기 등이 있다.
파라미터parameter
선형 회귀 모델에 사용되는 편향과 가중치 파라미터처럼 모델 훈련중에 학습되는 값들을 가리킨다. 모델 훈련을 통해 학습된 파라미터는 훈련된 모델 객체의 속성으로 저장된다.
스텝step
모델이 파라미터를 한 번 업데이트 하는 과정을 가리킨다. 배치 크기 \(m\) 만큼의 샘플에 대해 예측값을 계산한 후에 비용 함수를 이용하여 성능을 평가한 후에 비용 함수의 값, 즉 손실값을 줄이는 방향으로 파라미터를 한 번 업데이트 하는 과정이다.
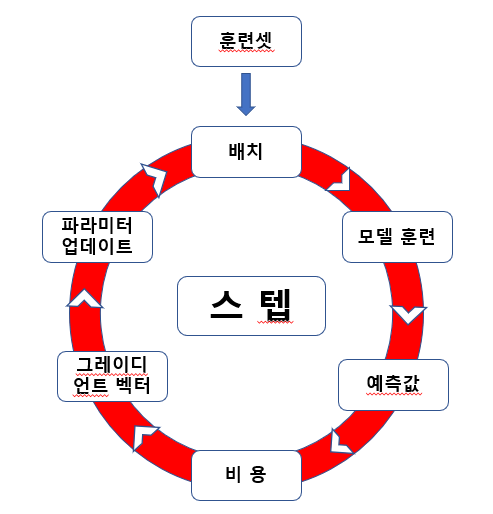
SGDRegressor 모델은 크기가 1인 배치로 훈련하기에 하나의 스텝에 하나의 데이터 샘플만 활용한다.
즉, 아래 과정으로 구성된 스텝을 훈련셋에 포함된 각각의 샘플에 대해 반복해서 진행한다.
하나의 데이터 샘플에 대한 예측값 계산
MSE 계산
MSE의 그레이디언트 계산
\(\theta\) 업데이트
배치 크기
파라미터를 한 번 업데이트 하기 위해 사용된 훈련 데이터 샘플의 개수를 가리킨다. 즉, 한 번의 스텝에서 사용되는 훈련 샘플의 개수다.
사이킷런 모델: 배치 크기 선택 옵션을 지원하지 않음. 경사하강법을 적용하는 모든 모델의 배치 크기는 1로 지정됨.
LinearRegression: 경사하강법 사용하지 않음.SGDRegressor: \(m = 1\)LogisticRegressor: \(m = 1\)
딥러닝 심층 신경망 모델: 배치 크기 선택 옵션을 제공함. 일반적으로 8, 16, 32, 64, 128, 256 중에 하나 선택.
비용 함수
평균 제곱 오차(MSE)처럼 모델의 성능이 얼마나 나쁜가를 계산하는 함수다. 훈련 스텝에서 비용 함수의 값, 즉 손실값은 배치 단위로 계산된다.
회귀 모델의 배치 단위로 계산되는 손실값은 평균 제곱 오차(MSE)로 계산된다.
예를 들어
SGDRegressor 모델은 크기가 1인 배치로 훈련하기에
매 스텝에서 아래 MSE 계산을 임의로 선택된 샘플 \(\mathbf{x}^{(i)}\) 대해 실행한다.
비용 함수의 그레이디언트 벡터gradient vector
비용 함수 \(\mathrm{MSE}(\mathbf{\theta})\)의 \(\mathbf{\theta}\)에 대한 미분값을 그레이디언트 벡터라 부르며 \(\nabla_\mathbf{\theta} \textrm{MSE}(\mathbf{\theta})\)로 표기한다. 그레이디언트 벡터는 파라미터 \(\mathbf{\theta}\)의 크기를 어떻게 업데이트 해야 하는가에 대한 정보를 제공한다.
학습률(\(\eta\))
훈련 스텝마다 파라미터 \(\mathbf{\theta}\)를 얼만큼씩 조정할 것인지를 정하는 비율이다.
에포크epoch
훈련셋에 포함된 모든 데이터를 대상으로 예측값을 한 번 계산하는 과정이다. 이 과정동안 실행된 스텝 회수만큼 파라미터의 업데이트가 이루어진다.
스텝 횟수
에포크 동안 실행된 스텝의 횟수, 즉 파라미터를 조정한 횟수다. 다음이 성립한다.
스텝 횟수 = (훈련셋 크기) / (배치 크기)
예를 들어, 훈련셋 크기가 1,000이고 배치 크기가 10이면 에포크마다 100번의 스텝이 실행된다.
반면에 SGDRegressor 모델은 크기가 1인 배치로 훈련하기에 한 번의 에포크동안 훈련셋 크기만큼의 스텝이 진행된다.
최적 학습 모델
비용 함수의 값, 즉 손실값을 최소화하는 파라미터를 학습한(찾아낸) 모델이며, 최종적으로 훈련을 통해 얻고자 하는 모델이다.
전역/지역 최소값
비용 함수의 전역/지역 최소값이다. 예를 들어 선형 회귀 모델의 경우엔 평균 제곱 오차(MSE) 함수가 갖는 전역/지역 최소값을 가리킨다.
허용 오차tolerance
보통 5 에포크 정도 반복 훈련이 지나도록 비용 함수의 그레이디언트 벡터의 크기가 허용 오차보다 작아지면 훈련을 종료시킨다. 이유는 그레이디언트 벡터의 크기가 매우 작으면 비용 함수의 \(\theta\)에 대한 그래프가 매우 완만해졌음을, 따라서 비용 함수의 값, 즉 손실값이 거의 변하지 않음을 의미하기 때문이다. 결론적으로 비용 함수의 전역 또는 지역 최소값을 계산하는 파라미터 \(\theta\)가 거의 학습되었음을 의미한다.
4.2.1. 선형 회귀 모델 훈련과 경사하강법#
MSE를 비용 함수로 사용하는 선형 회귀 모델의 파라미터를 조정하는 과정을 이용하여 경사하강법의 기본 아이디어를 설명한다.
선형 회귀 모델 훈련에 사용되는 경사하강법은 아래 과정으로 구성된다.
\(\mathbf{\theta}\)를 임의의 값으로 지정한 후 훈련을 시작한다.
지정된 에포크만큼 또는 그레이디언트 벡터 \(\nabla_\mathbf{\theta} \textrm{MSE}(\mathbf{\theta})\)가 허용 오차보다 작아질 때까지 아래 과정으로 구성된 훈련 스텝을 반복한다.
배치 크기 \(m\) 만큼의 훈련 샘플을 이용해서 예측값 생성 후 \(\mathrm{MSE}(\mathbf{\theta})\) 계산.
\(\mathbf{\theta}\)를 아래 점화식을 이용하여 업데이트
그레이디언트 벡터의 방향과 크기
그레이디언트 벡터 \(\nabla_\mathbf{\theta} \textrm{MSE}(\mathbf{\theta})\)가 가리키는 방향의 반대 방향으로 움직이면 빠르게 \(\textrm{MSE}(\mathbf{\theta})\)가 전역 최소값을 갖는 \(\mathbf{\theta}\) 접근한다.
아래 그림은 \(\mathbf{\theta}\)에 대한 2차 다항식 함수로 계산되는 비용 함수의 그래프상의 한 점에서의 기울기가 양수인 경우 음수쪽으로 움직여야 전역 최소값으로 수렴하는 것을 보여준다.
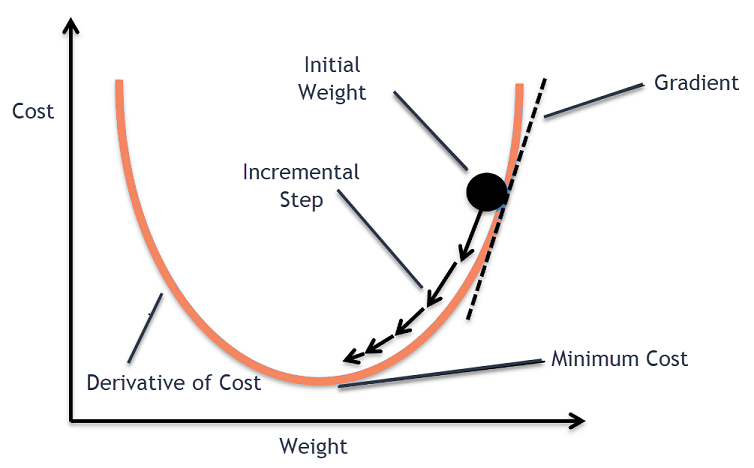
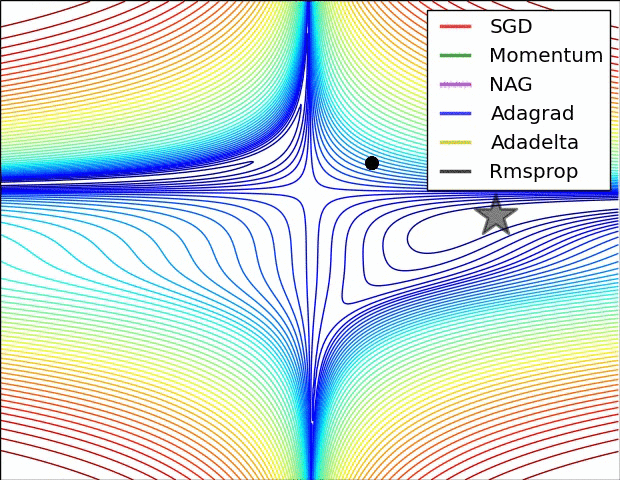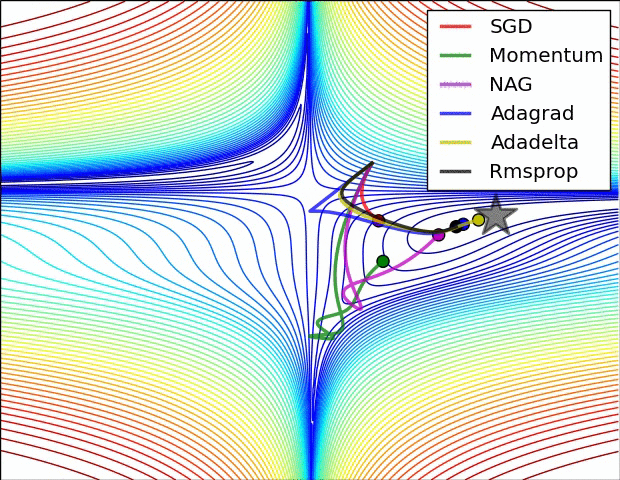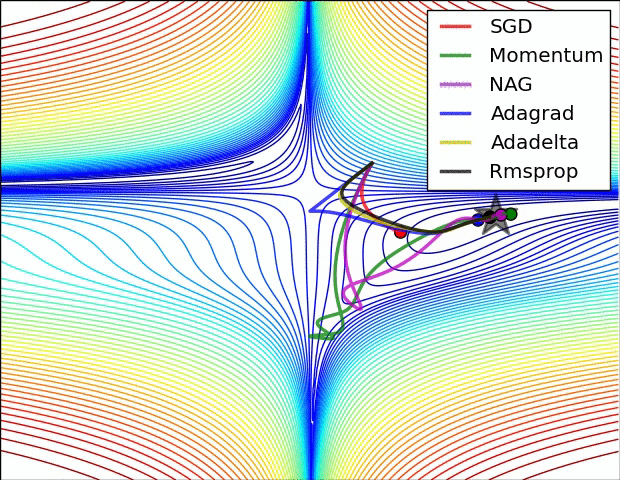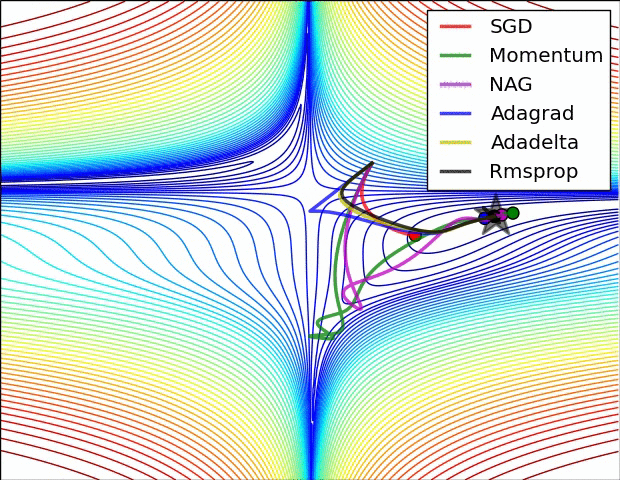
아래 두 그림은 산에서 가장 경사가 급한 길을 따를 때 가장 빠르게 하산한다는 원리를 보여준다. 이유는 해당 지점에서 그레이디언트 벡터를 계산하면 정상으로 가는 가장 빠른 길을 안내할 것이기에 그 반대방향으로 움직여야 하기 때문이다. 그림에서 보여지는 여러 경로는 경사하강법을 담당하는 여러 알고리즘에 따라 선택된다.
|
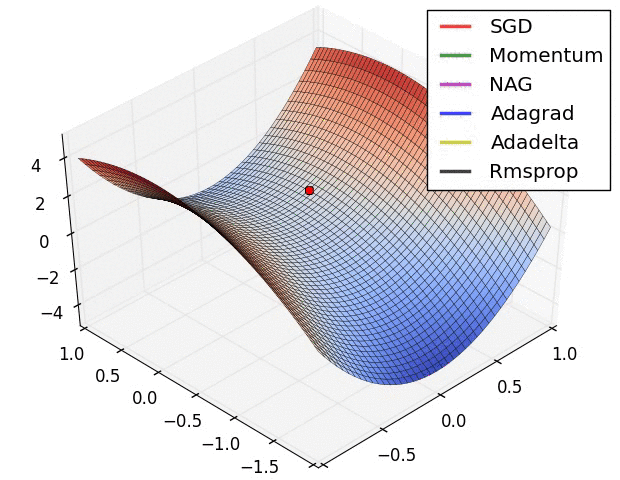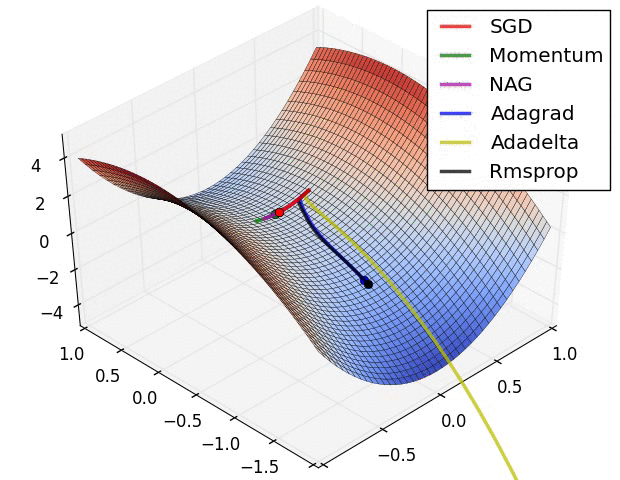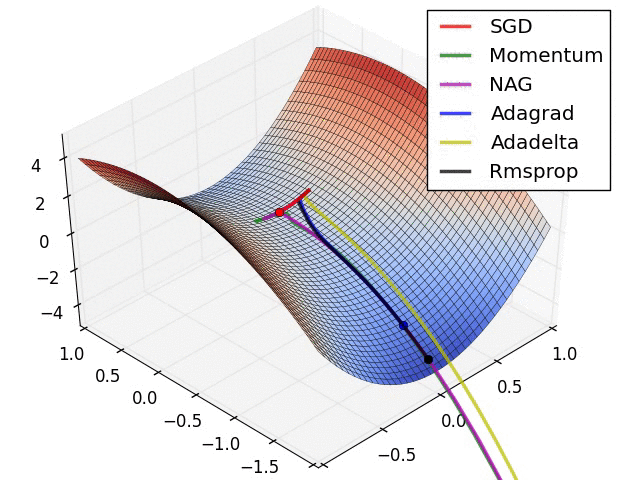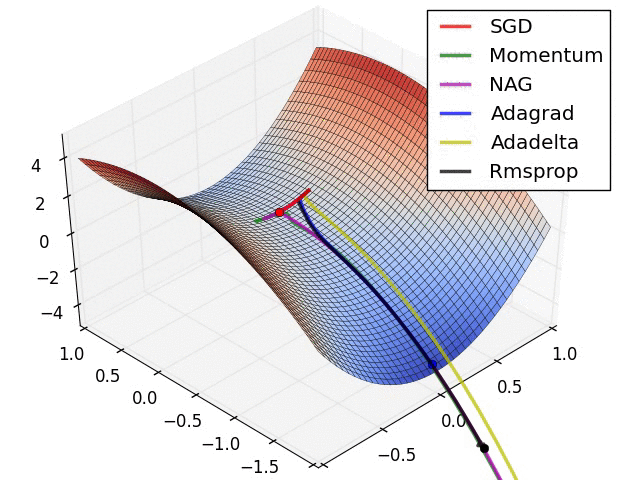
|
4.2.2. 학습률의 중요성#
선형 회귀 모델은 적절할 학습률로 경사하강법으로 적용하여 훈련될 경우 빠른 시간에 비용 함수가 전역 최소값을 갖도록 하는 \(\hat{\theta}\) 에 수렴한다.
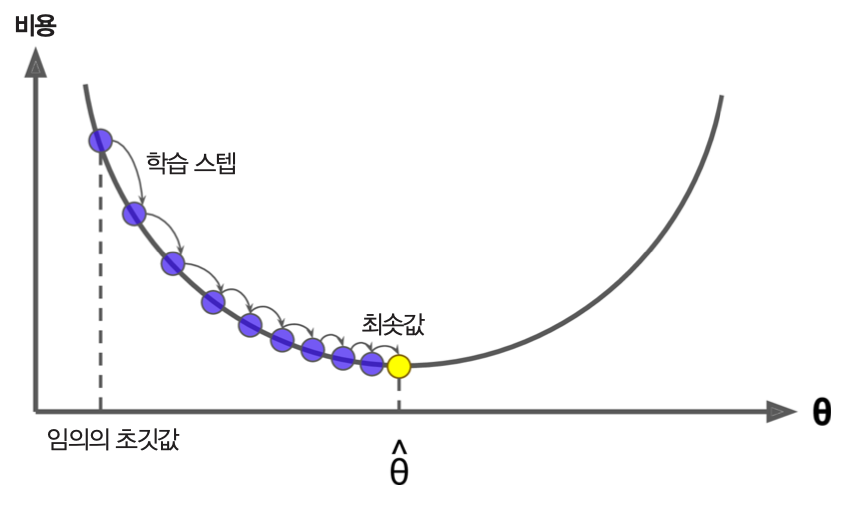
반면에 학습률이 너무 작거나 너무 크면 비용 함수가 전역 최소값을 갖도록 하는 파라미터에 너무 느리게 수렴하거나 아예 수렴하지 않을 수도 있다.
학습률이 너무 작은 경우: 비용 함수가 전역 최소값을 갖도록 하는 \(\hat{\theta}\) 에 너무 느리게 수렴.
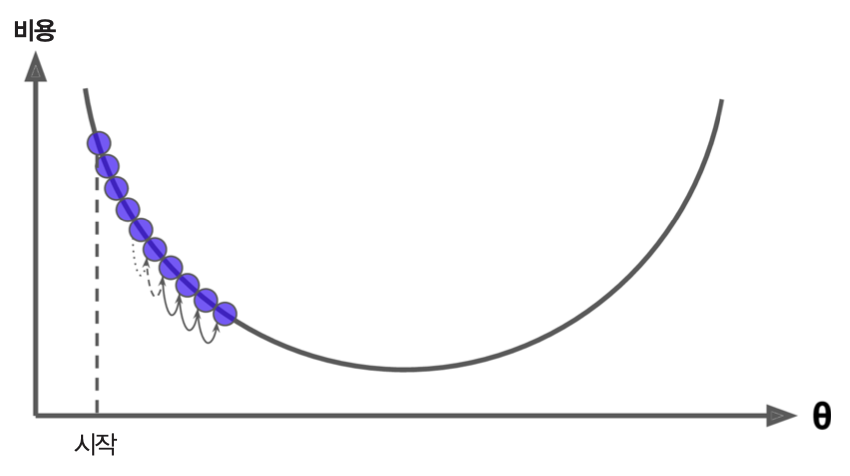
학습률이 너무 큰 경우: 비용 함수가 전역 최소값을 갖도록 하는 \(\hat{\theta}\) 에 수렴하지 않고 발산함
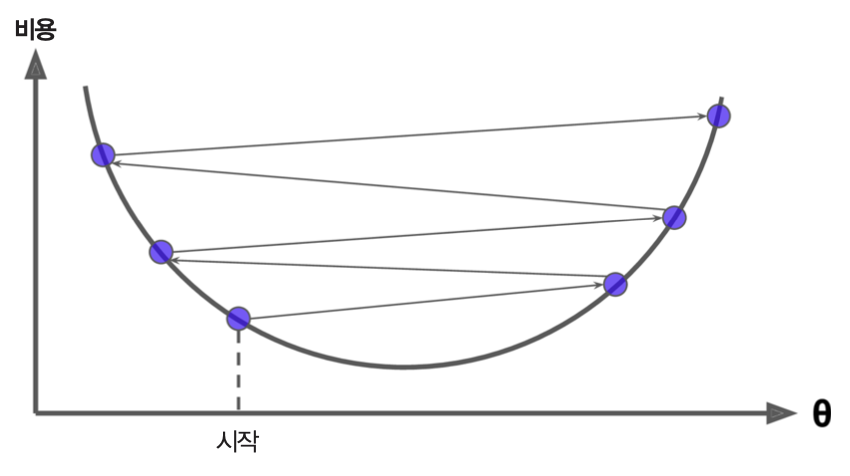
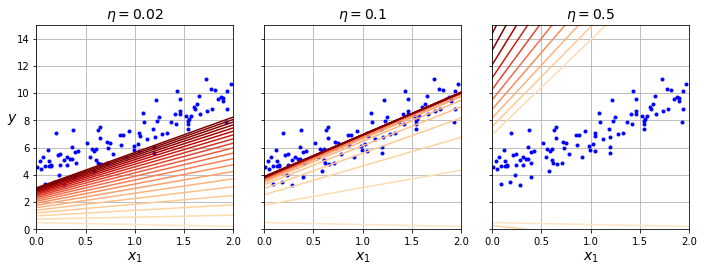
아래 세 그림은 학습률에 따라 선형 회귀 모델이 최적의 모델로 수렴하는지 여부와 수렴 속도가 달라지는 것을 잘 보여준다.
\(\eta = 0.02\): 학습률이 너무 작은 경우
\(\eta = 0.1\): 학습률이 적절한 경우
\(\eta = 0.5\): 학습률이 너무 큰 경우
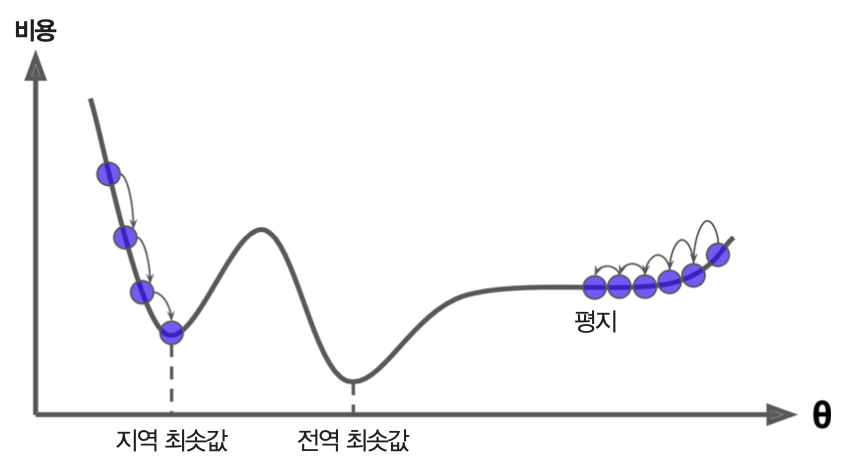
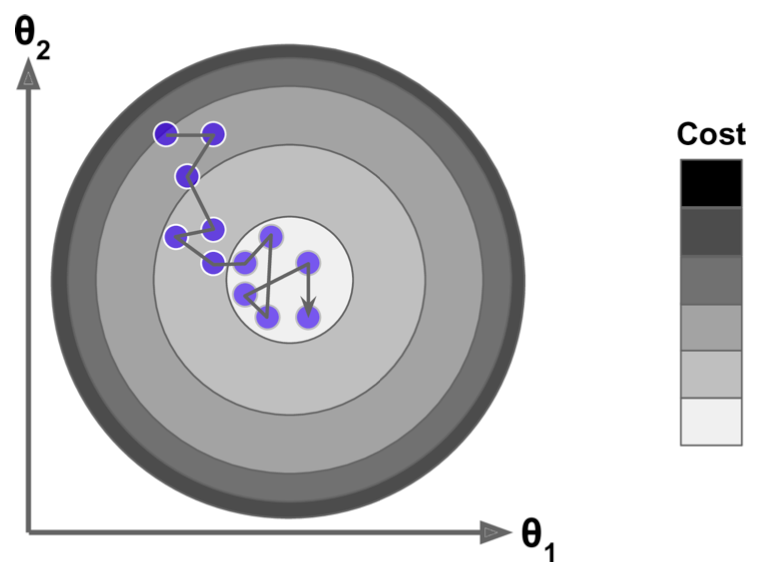
비선형 모델 훈련의 어려움
선형 회귀 모델은 학습률을 적절하게 잡으면 언제나 최적의 모델로 수렴한다. 아래 그림은 비선형 모델의 경우엔 하지만 학습률과 상관 없이 파라미터를 초기화하는 방식에 따라 지역 최소값에 수렴하거나 수렴하지 못하고 정체할 수도 있음을 잘 보여준다.
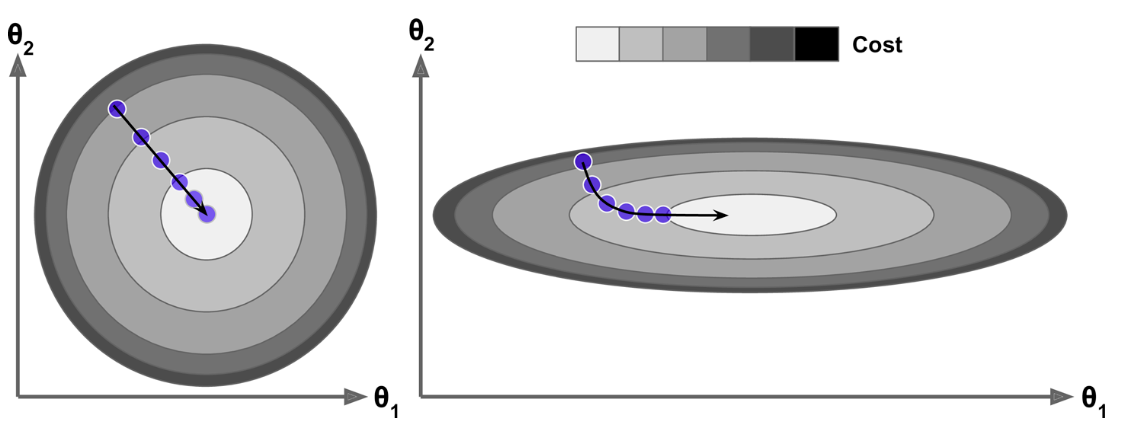
특성 스케일링의 중요성
특성들의 스켈일을 통일시키면 보다 빠른 학습이 이루어지는 이유를 아래 그림이 설명한다.
왼편 그림: 두 특성의 스케일이 동일하게 조정된 경우엔 비용 함수의 최소값으로 최단거리로 수렴한다. 비용 등고선이 원 모양으로 그려지는 경우를 생각하면 된다.
오른편 그림: 두 특성의 스케일이 다른 경우 비용 함수의 최소값으로 보다 먼 거리를 지나간다. 이런 경우엔 비용 등고선이 타원 모양 또는 찌그러진 모양으로 그려지기 때문이다.
4.2.3. 경사하강법 종류#
모델 훈련에 사용되는 경사하강법은 훈련 대상 모델을 지정할 때 사용하는 하이퍼파라미터 중의 하나인 배치 크기에 따라 세 종류로 나뉜다.
배치 경사하강법
에포크마다 한 번 그레이디언트를 계산하여 파라미터를 조정(업데이트)한다. 즉, 배치 크기(\(m\))가 전체 훈련셋의 크기와 같다. 즉, 스텝의 크기가 1이다.
파라미터 업데이트를 에포크에 한 번만 수행 하기에 모델을 지정할 때 에포크를 크게 잡아야 한다. 그렇지 않으면 훈련이 제대로 진행하지 않는다. 그런데 훈련셋이 크면 그레이디언트를 계산하는 데에 많은 시간과 메모리가 필요해지는 문제가 발생할 수 있다. 이와 같은 이유로 인해 사이킷런을 포함하여 일반적으로 배치 경사하강법을 지원하지 않는다.
확률적 경사하강법(SGD)
배치 크기(\(m\))가 1인 경상하강법을 가리킨다. 즉, 하나의 훈련 셈플에 대한 예측값을 계산한 다음에 바로 비용 함수의 그레이디언트를 계산하여 파라미터를 조정한다.
스텝에서 사용되는 샘플은 무작위로 선택된다. 따라서 경우에 따라 하나의 에포크에서 여러 번 선택되거나 전혀 선택되지 않는 샘플이 존재할 수도 있지만, 이는 별로 문제되지 않는다.
확률적 경사하강법의 장점은 계산량이 매우 적다는 점이다. 따라서 아주 큰 훈련셋을 이용하여 훈련할 수 있다. 특히 훈련셋이 너무 커서 조금씩 메모리로 불러와서 훈련을 진행하는 외부 메모리 학습out-of-core learning에 활용될 수 있다.
또한 파라미터 조정이 불안정하게 이뤄질 수 있기 때문에 지역 최소값에 상대적으로 덜 민감하다. 반면에 동일한 이유로 경우에 따라 전역 최소값에 수렴하지 못하고 주변을 맴돌 수도 있다.
요동치는 파라미터를 제어하기 위해 학습률을 학습 과정 동안 천천히 줄어들도록 하는 학습 스케줄learning schedule을 사용한다. 학습 스케줄은 일반적으로 훈련 에포크가 진행될 수록 학습률이 조금씩 작아지도록 지정한다.
Example 4.1 (사이킷런의 SGDRegressor 모델 선언)
확률적 경사하강법을 사용하는 선형 회귀 모델이다. 아래 코드는 에포크 크기, 허용 호차, 학습 스케줄, 규제 적용 여부를 지정하는 하이퍼파라미터를 함께 사용하는 것을 보여준다.
SGDRegressor(penalty=l2,
max_iter=1000,
tol=1e-3,
eta0=0.01,
early_stoppingbool=False,
n_iter_no_change=5,
random_state=42)
penalty=l2: 규제 종류.None은 규제 미사용 없음 (추후 설명)max_iter=1000: 최대 에포크 수tol=1e-3: 허용 오차. 손실값이n_iter_no_change만큼의 에포크 동안 허용 오차보다 작게 변할 때 훈련 중지.early_stoppingbool이False이면 훈련셋에 대한 손실값을,True이면 자동으로 분리된 검증셋의 손실값이 사용됨.
early_stoppingbool=False: 조기 종료 여부 지정. 기본값은False. (추후 설명)eta0=0.01: 초기 학습률. 학습 스케줄에 활용됨n_iter_no_change=5: 지정된 에포크 동안loss > best_loss - tol상태가 유지되면 훈련 중지
미니 배치 경사하강법
배치 크기(\(m\))를 2 이상으로 잡는 경사하강법이다. 보통 2에서 수백 사이로 정한다. 배치 크기를 적절히 크게 잡으면 확률적 경사하강법(SGD) 보다 파라미터의 움직임이 덜 불규칙적이 되며, 배치 경사하강법보다 훨씬 빠르게 최적 학습 모델에 수렴한다. 다만 SGD에 비해 지역 최소값에 수렴할 위험도가 보다 커질 수 있다. 하지만 대부분의 딥러닝 심층 신경망 모델에서 지원된다.
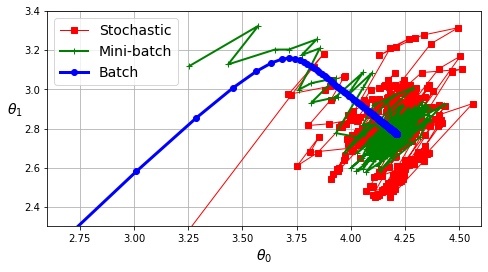
세 경사하강법 비교
아래 그림은 앞서 배치/확률적/미니 배치 경사하강법을 진행할 때 학습되는 파라미터들의 변화 과정을 보여준다.
배치 경사하강법 파라미터 변화: 진동없이 최적 파라미터에 수렴. 하지만 훈련 시간이 가장 길고, 큰 훈련셋에서는 적용할 수 없음.
확률적 경가하강법 파라미터 변화: 진동 심함. 최적 파라미터 근처에서 계속 진동하고 수렴하지 못함. 하지만 학습 시간이 매우 짧아서 대용량 훈련셋에 대해 잘 작동함.
미니 배치 경사하강법 파라미터 변화: 진동이 상대적으로 약하며 나름 최적 파라미터에 잘 접근함. 학습 스케줄을 이용하여 훈련이 진행될 수록 학습률을 줄이면 최적 파라미터에 가깝게 근접함.
4.3. 비선형 데이터 학습: 다항 회귀#
비선형 데이터를 선형 회귀를 이용하여 학습하는 기법을 다항 회귀polynomial regression라 한다.
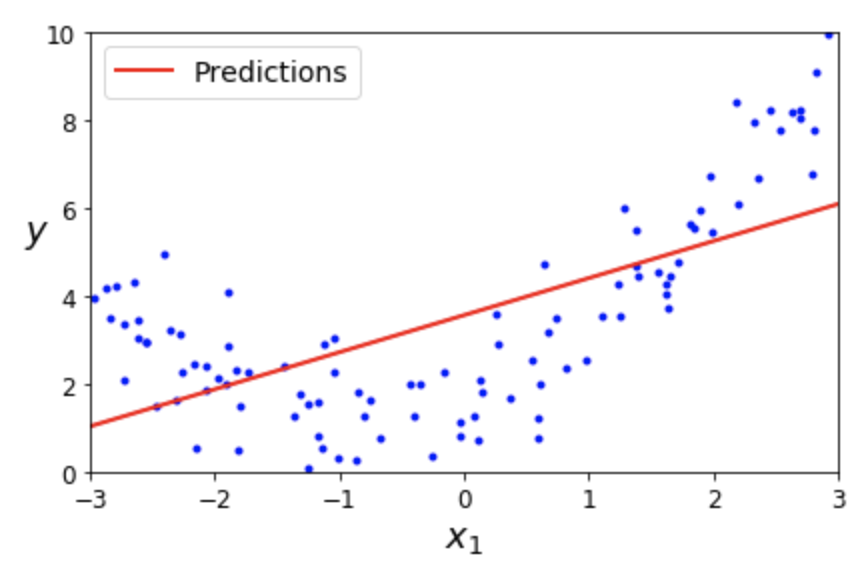
예제: 2차 함수 모델를 따르는 데이터셋에 선형 회귀 모델 적용
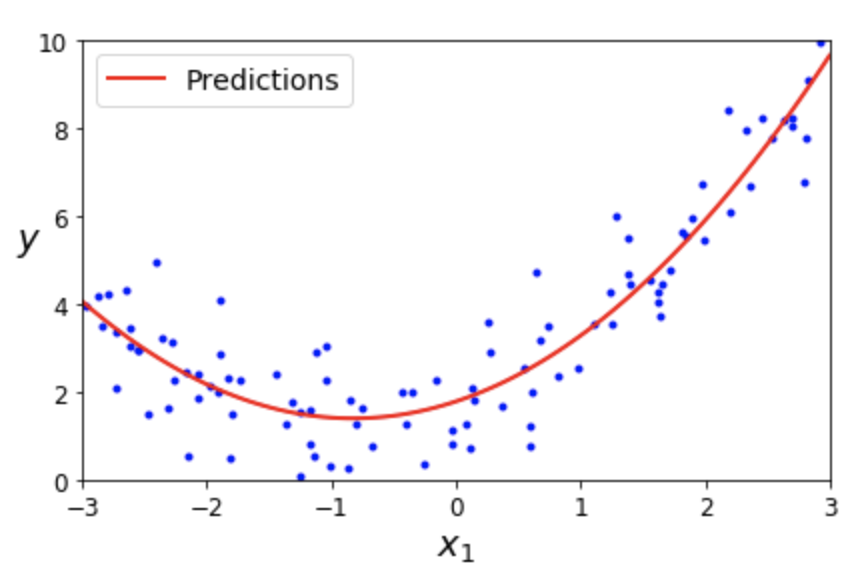
아래 그림은 2차 함수의 그래프 형식으로 분포된 데이터셋을 선형 회귀 모델로 학습시킨 결과를 보여준다.
예제: 2차 함수 모델를 따르는 데이터셋에 2차 다항식 모델 적용
반면에 아래 그림은 \(x_1^2\) 에 해당하는 특성을 새로이 추가한 후에 선형 회귀 모델을 학습시킨 결과를 보여준다.
사이킷런의 PolynomialFeatures 변환기
지정된 차수의 다항식에 포함되어야 하는 특성을 생성하여 추가하는 변환기다.
PolynomialFeatures(degree=d, include_bias=False)
degree=d는 몇 차 다항식을 활용할지 지정하는 하이퍼파라미터다.
include_bias=False는 편향에 활용되는 1을 특성으로 추가하지 않는다는 의미이다.
원래는 include_bias=True가 기본값이기에 모든 샘플에 1을 0번 특성으로 추가해야 하지만
여기서는 LinearRegression 모델에 의해 편향이 별도로 다뤄지기 때문에 굳이 먼저 추가하지
않아도 된다.
Example 4.2 (2차 다항 회귀)
기존에 \(x_1, x_2\) 두 개의 특성을 갖는 데이터셋에 대해 2차 다항식 모델을 훈련시키고자 하면 \(d=2\)으로 설정한다. 그러면 \(x_1, x_2\) 을 이용한 2차 다항식에 포함될 항목을 새로운 특성으로 추가해야 한다. 즉, \((x_1+x_2)^2\)의 항목에 해당하는 다음 3 개의 특성을 추가해야 함을 의미한다.
위 특성들에 선형 회귀 모델을 훈련시키면 예측값은 아래와 같이 계산된다.
다항 회귀의 단점
몇차 다항 회귀를 사용해야 할지 일반적으로 알 수 없다. 또한 심층 신경망처럼 비선형 데이터를 분석하는 보다 좋은 모델이 개발되어 굳이 다항 회귀를 사용할 필요가 없어졌다. 여기서는 비선형 데이터 분석을 선형 회귀 모델로 제대로 예측할 수 없음을 보여주기 위해 언급되었다.
4.4. 과소/과대 적합 여부 판단#
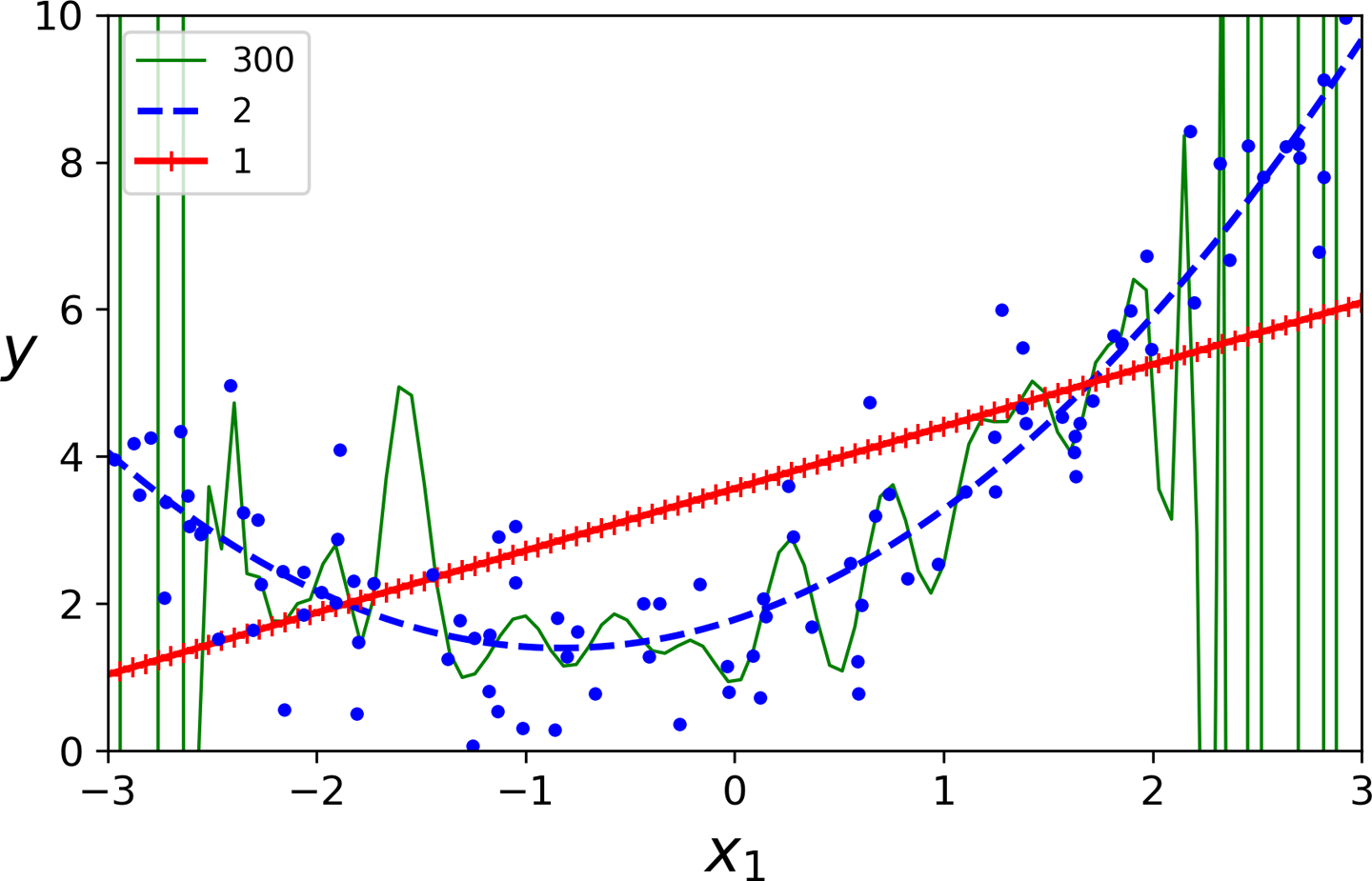
사용되는 모델에 따라 훈련된 모델의 성능이 많이 다를 수 있다. 아래 그림은 기본 선형 모델은 성능이 너무 좋지 않은 반면에 300차 다항 회귀 모델은 너무 과하게 훈련 데이터에 민감하게 반응하는 것을 보여준다. 반면에 2차 다항 회귀 모델이 적절(?)하게 예측값을 계산하는 것으로 보인다.
모델 성능 평가: 교차 검증
일반적으로 어떤 모델이 가장 좋은지 미리 알 수 없다. 따라서 보통 다양한 모델을 대상으로 교차 검증을 진행하여 성능을 평가한다. 교차 검증 결과에 따른 모델 평가는 다음 두 종류로 나뉜다.
과소적합: 훈련 점수와 교차 검증 점수 모두 낮은 경우
과대적합: 훈련 점수는 높지만 교차 검증 점수가 상대적으로 많이 낮은 경우
과소 적합 모델 개선법
모델이 데이터셋에 과소 적합 하는 일반적인 경우와 개선법은 다음과 같다.
너무 단순한 모델 활용: 보다 복잡한 데이터를 학습할 수 있는 모델 활용
너무 적은 데이터: 훈련셋 양 늘리기
과대 적합 모델 개선법
모델 규제 적용: 모델이 훈련중에 데이터에 너무 민감하게 반응하지 않도록 규제 가함. 이어지는 내용 참고
보다 많은 데이터: 데이터가 많을 수록 일반적으로 과대 적합이 덜 발생함.
모델의 일반화 성능
훈련 과정에서 다루지 않은 새로운 데이터 대한 예측 능력이 모델의 일반화 성능이다. 새로운 데이터에 대한 모델의 예측에 나쁜 영향을 미치는 요소는 일반적으로 다음 세 가지가 있다.
편향: 실제로는 2차원 모델인데 1차원 모델을 사용하는 경우처럼 데이터의 분포에 대한 잘못된 가정으로 인해 발생한다. 과소 적합이 발생할 가능성이 매우 높다.
분산: 모델이 훈련 데이터에 민감하게 반응하는 정도를 가리킨다. 고차 다항 회귀 모델처럼 모델이 학습해야하는 파라미터의 수가 많을 수록, 즉 모델의 자유도degree of freedom가 높을 수록 분산이 커진다.
제거 불가능 오류: 잡음(noise) 등 데이터 자체의 한계로 인해 발생한다. 데이터 전처리 과정에서 잡음 등을 제거해야만 오류를 줄일 수 있다.
편향-분산 트레이드오프
복잡한 모델일 수록 편향을 줄어들지만 분산은 커지는 현상을 가리킨다.
4.5. 모델 규제와 조기 종료#
훈련 중에 과소 적합이 발생하면 보다 복잡한 모델을 선택해야 한다. 반면에 과대 적합이 발생할 경우 보다 단순한 모델을 사용하거나 모델에 규제를 가해서 모델의 분산을 줄여 과대 적합을 방지하거나 과대 적합이 최대한 늦게 발생하도록 유도해야 한다.
4.5.1. 모델 규제#
회귀 모델에 대한 규제regularization는 가중치의 역할을 제한하는 방식으로 이루어지며, 방식에 따라 다음 세 가지 회귀 모델이 지정된다.
릿지 회귀
라쏘 회귀
엘라스틱 넷
릿지 회귀Ridge Regression
아래 비용 함수를 사용한다.
\(\theta_0\): 규제에서 제외.
\(m\): 배치 크기
\(\alpha\)(알파): 규제 강도.
\(\alpha=0\)일 때 규제 없음.
\(\alpha\) 가 커질 수록 가중치의 역할이 줄어듦. 비용을 줄이기 위해 가중치를 작게 유지하도록 훈련되어 결국 모델의 분산 정도가 작아짐.
StandardScaler 등을 사용하여 특성 스케일링을 진행 한 다음에
규제를 적용해야 모델의 성능이 좋아진다.
이유는 \(\theta_i\) 값이 특성의 크기에 의존하기에
모든 특성의 크기를 비슷하게 맞추면 \(\theta_i\)가
보다 일정하게 수렴하기 때문이다.
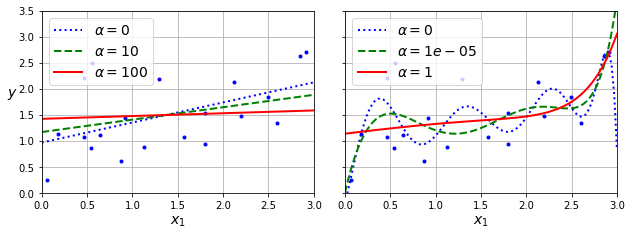
아래 그림은 서로 다른 규제 강도를 사용한 릿지 회귀 모델의 훈련 결과를 보여준다.
왼편: 선형 회귀 모델에 세 개의 \(\alpha\) 값 적용.
오른편: 10차 다항 회귀 모델에 세 개의 \(\alpha\) 값 적용.
라쏘 회귀Lasso Regression
아래 비용 함수를 사용한다.
별로 중요하지 않은 특성에 대해 \(\theta_i\)가 빠르게 0에 수렴하도록 훈련 중에 유도된다. 이유는 \(\mid \theta_i \mid\) 의 미분값이 1 또는 -1 이라는 상대적으로 큰 값이기에 파라미터 업데이트 과정에서 보다 작은 \(\mid \theta_i \mid\)가 보다 빠르게 0에 수렴하기 때문이다.
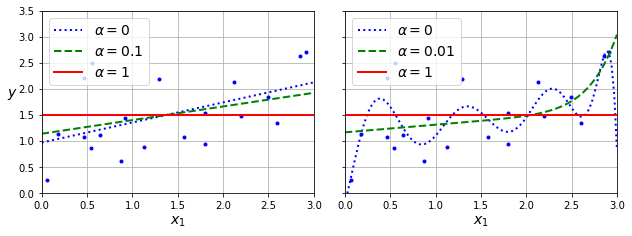
아래 그림은 서로 다른 규제 강도를 사용한 라쏘 회귀 모델의 훈련 결과를 보여준다.
왼편: 선형 회귀 모델에 세 개의 \(\alpha\) 값 적용.
오른편: 10차 다항 회귀 모델에 세 개의 \(\alpha\) 값 적용.
엘라스틱 넷Elastic Net
릿지 회귀와 라쏘 회귀를 절충한 아래 비용 함수를 사용한다.
\(r\): 릿지 회귀에 사용되는 규제와 라쏘 회귀에 사용되는 규제의 사용 비율
규제 강도를 의미하는 \(\alpha\)가 각 규제에 가해지는 정도가 다름에 주의할 것.
규제 선택
약간이라도 규제를 사용해야 하며, 일반적으로 릿지 회귀가 추천된다. 반면에 유용하지 않은 속성이 많다고 판단되는 경우엔 라쏘 회귀 또는 엘라스틱 넷이 추천된다. 하지만 특성 수가 훈련 샘플 수보다 많거나 특성 몇 개가 상호 강하게 연관되어 있는 경우엔 엘라스틱 넷을 추천한다.
4.5.2. 조기 종료#
조기 종료early stopping는 모델이 훈련셋에 과대 적합하는 것을 방지하기 위해 훈련을 적절한 시기에 중단시키는 기법이며, 가장 많이 사용된다. 조기 종료는 검증셋에 대한 비용 함수의 값, 즉 검증셋에 대한 손실값이 더 이상 제대로 줄어들지 않으면 바로 훈련을 종료한다.
아래 그래프는 2차 함수 곡선 형식으로 분포된 데이터셋에 90차 다항 회귀 모델을 훈련시킨 결과를 보여준다. 실행된 에포크가 많아질 수록 훈련셋에 대한 모델의 비용(RMSE)이 점차 낮아지는 반면에 검증셋에 대한 비용은 250 에포크 정도 지나면서 늘기 시작한다. 즉, 모델이 훈련셋에 과하게 적응하기 시작했고, 이는 모델의 일반화 성능이 떨어지기 시작함을 의미한다. 따라서 허용된 최대 500 에포크를 훈련하지 않고 250 에포크 정도에서 훈련을 멈추도록 하는 게 조기 종료다.
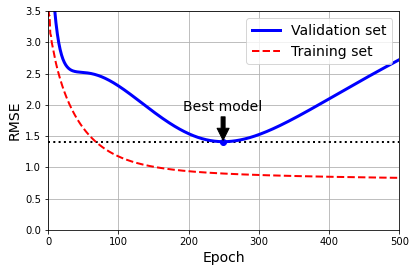
확률적 경사하강법, 미니 배치 경사하강법에서는 비용 함수의 값, 즉 손실값이 보다 많이 진동하기에 비용이 언제 최소가 되었는지 알기 어렵다. 따라서 한동안, 보통 5 에포크 정도, 그동안의 훈련동안 기록된 최소의 손실값보다 새로 계산된 손실값이 높게 유지될 때 훈련을 멈추고 그동한 기록된 최소의 손실값 계산에 사용된 최적의 파라미터를 사용하는 모델로 되돌린다.
사이킷런의 SGDRegressor 모델은 위에서 언급한 early_stopping 하이퍼파라미터의 값을 True로 지정하면
훈련셋의 일부를 검증셋으로 진행한 다음에 조기 종료 기능을 갖춘 상태로 훈련을 진행한다.
4.6. 로지스틱 회귀#
로지스틱 회귀는 회귀 모델의 결과를 분류 모델로 활용할 수 있도록 해주며 분류 모델에서 가장 중요한 역할을 수행한다. 로지스틱 회귀는 이진 분류에 사용되며, 다중 클래스 분류에는 로지스틱 회귀을 일반화한 소프트맥스 회귀가 사용된다.
4.6.1. 시그모이드 함수#
로지스틱 회귀는 선형 회귀 방식으로 계산된 예측값을 시그모이드 함수에 적용하여 0과 1 사이로 변환된 값을 모델의 최종 예측값으로 활용한다.
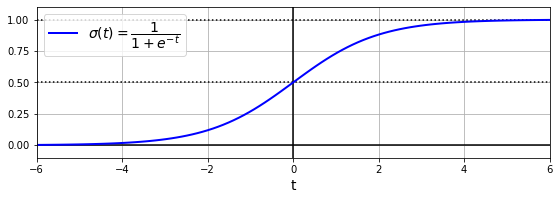
시그모이드sigmoid 함수는 다음과 같이 정의된다.
그래프로 그리면 \(t=0\)일 때 0.5를 갖고, \(t\)가 양의 무한대로 커질 수록 1에 수렴하고 음의 무한대로 커지면 -1에 수렴한다.
확률 예측
로지스티 회귀 모델은 먼저 선형 회귀 모델이 예측한 값에 시그모이드 함수를 적용하여 0과 1 사이의 값, 즉 양성일 확률 \(\hat p\) 를 계산한다.
예측값
로지스틱 회귀 모델의 예측값은 계산된 확률이 0.5 이상인지 여부로 결정한다.
이는 다음과 같이 가중치와 특성의 선형 조합 결과가 0 이상인지 여부에 따라 양성 또는 음성으로 판별함을 의미한다.
양성: \(\theta_0 + \theta_1\, x_1 + \cdots + \theta_n\, x_n \ge 0\) 인 경우
음성: \(\theta_0 + \theta_1\, x_1 + \cdots + \theta_n\, x_n < 0\) 인 경우
4.6.2. 로그 손실 함수#
로지스틱 회귀 모델은 아래 로그 손실log loss 함수를 비용 함수로 사용한다.
그러면 양성 샘플에 대해서는 1에 가까운 확률값을, 음성 샘플에 대해서는 0에 가까운 확률값을 내도록 훈련한다. 실제로 양성 샘플에 대해 0에 가까운 값을 예측하거나, 음성 샘플에 대해 1에 가까운 값을 예측하면 비용 함수의 값이 매우 커지게 된다.
로그 손실 함수 이해
틀린 예측을 하면 로그 손실값이 매우 커진다. 예를 들어 하나의 샘플에 대한 손실값은 다음과 같다.
아래 표는 예측을 틀리게 할 때 위 손실값이 무한히 커질 수 있음을 설명한다.
타깃 |
예측 확률 |
로그 손실 |
|---|---|---|
\(y = 1\) (양성) |
\(p \lt 0.5\) |
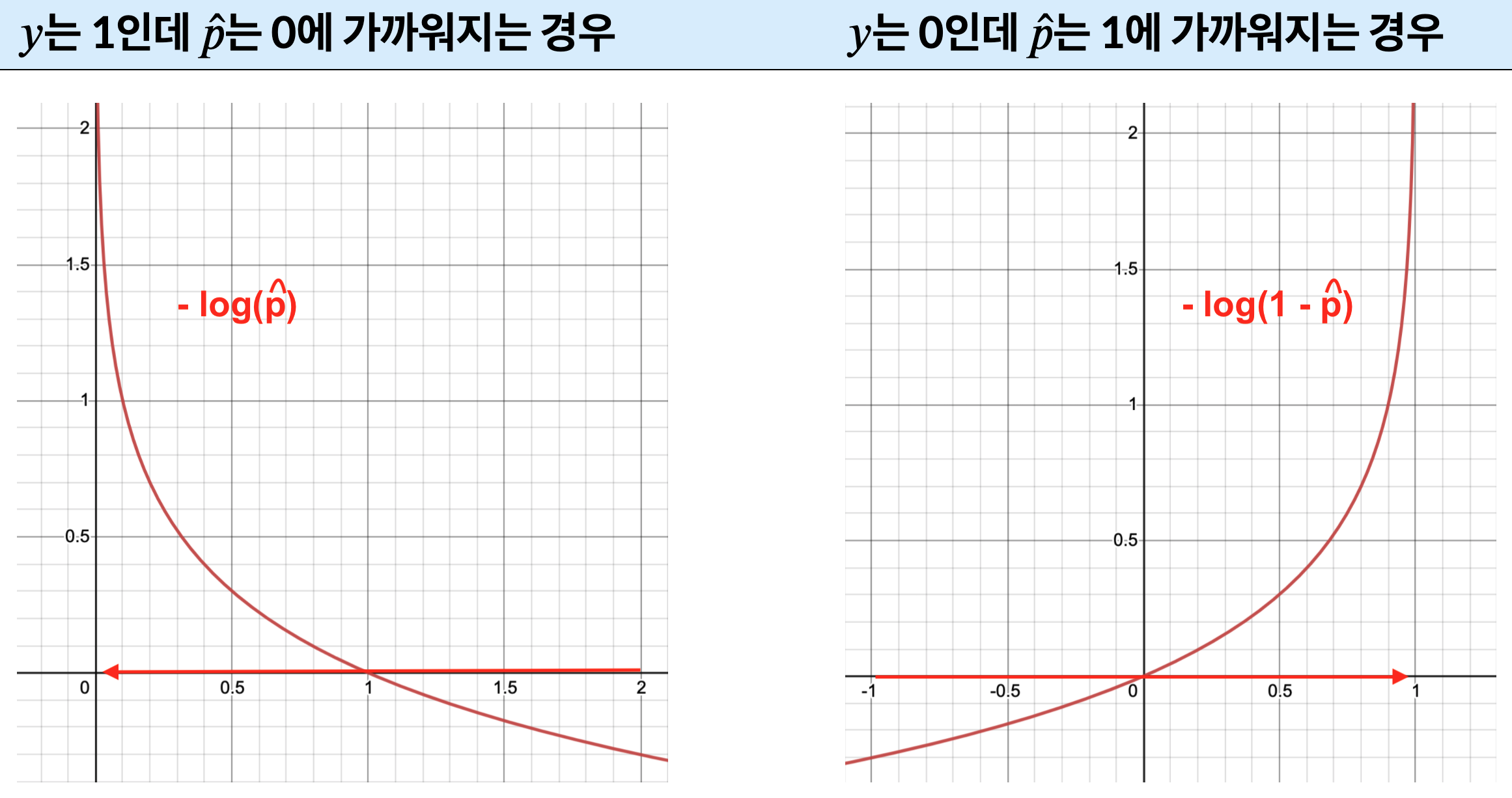
\(p\)가 0에 가까워질 수록,즉 더 많이 틀리게 예측할 수록 손실값 \(-\log(\,\hat p\,)\) 가 무한히 커짐(아래 왼쪽 그림). |
\(y = 0\) (음성) |
\(p \ge 0.5\) |
\(p\)가 1에 가까워질 수록,즉 더 많이 틀리게 예측할 수록 손실값 \(-\log(\,1-\hat p\,)\) 가 무한히 커짐(아래 오른쪽 그림). |
로그 손실 함수와 최적의 모델
훈련셋이 가우스 분포를 따른다는 전제하에 로그 손실 함수를 최소화하면 최적의 모델을 얻을 수 있다는 사실이 수학적으로 증명되었다. 상세 내용은 앤드류 응(Andrew Ng) 교수의 Stanford CS229 강의에서 확인할 수 있다.
4.6.3. 이진 분류 예제: 붓꽃 데이터셋#
붓꽃의 품종 분류를 로지스틱 회귀로 진행한다. 붓꽃 데이터셋의 샘플은 꽃받침sepal의 길이와 너비, 꽃입petal의 길이와 너비 등 총 4개의 특성으로 이루어진다.
[꽃받침 길이, 꽃받침 너비, 꽃잎 길이, 꽃잎 너비]

레이블은 0, 1, 2 중에 하나이며 각 숫자는 하나의 품종을 가리킨다.
0: Iris-Setosa(세토사)
1: Iris-Versicolor(버시컬러)
2: Iris-Virginica(버지니카)

붓꽃 데이터셋 불러오기
붓꽃 데이터셋은 머신러닝 분류 모델을 소개할 때 자주 활용되는 유명한 데이터셋이다. 많은 서이트에서 다운로드 서비스를 제공하지만 여기서는 사이킷런 자체로 제공하는 데이터셋을 불러온다.
from sklearn.datasets import load_iris
iris = load_iris(as_frame=True)
load_iris() 함수는 데이터셋을 사전 자료형과 유사한 Bunch 자료형으로 불러온다.
사용되는 키(key) 중에 data 키와 연결된 값이 4개의 특성으로 구성된 훈련셋 데이터프레임DataFrame이고
target 키와 연결된 값이 레이블셋 시리즈Series이다.
훈련셋의 처음 5개의 샘플은 다음과 같다.
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
품종의 실제 이름은 target_names 키의 값으로 지정되었으며 다음과 같이
setosa, versicolor, virginica 세 개의 품종이다.
array(['setosa', 'versicolor', 'virginica'], dtype='<U10')
4.6.4. 결정 경계#
버지니카 품종 감지기: 꽃잎 너비 특성 활용
로지스틱 회귀 모델을 이용하여 붓꽃의 품종이 버지니카인지 여부를 판별하는 이진 분류기를 훈련시켜 보자. 문제를 단순화하기 위해 꽃잎의 너비 특성 하나만 이용하여 붓꽃의 품종을 판별한다.
X = iris.data[["petal width (cm)"]].values
y = iris.target_names[iris.target] == 'virginica'
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
log_reg = LogisticRegression(random_state=42)
log_reg.fit(X_train, y_train)
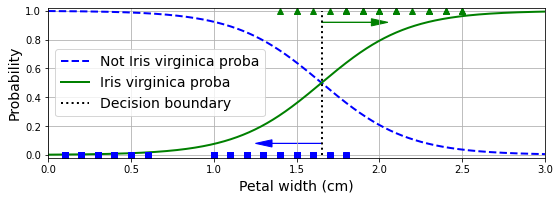
훈련 결과 꽃잎의 너비가 1.65cm 보다 크면 버지니카 품종일 가능성이 50% 이상으로 계산된다. 즉, 버지니카 품좀 감지기의 결정 경계decision boundary는 꽃잎 너비 기준으로 1.65cm 이다.
아래 그림의 초록 실선은 꽃잎 너비 1.65 기준으로 버지니카 품종일 확율이 50%를 넘어서는 것을 보여준다. 반면에 파랑 파선은 반대로 꽃잎 너비 1.65 기준으로 버니니카 품종이 아닐 확률이 50% 아래로 떨어지는 것을 보여준다.
버지니카 품종 감지기: 꽃잎 길이와 너비 특성 활용
이번에는 꽃잎의 길이와 너비 두 특성을 이용하여 붓꽃의 품종을 판별하는 로지스틱 회귀 모델을 훈련한다.
X = iris.data[["petal length (cm)", "petal width (cm)"]].values
y = iris.target_names[iris.target] == 'virginica'
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
log_reg = LogisticRegression(C=2, random_state=42)
log_reg.fit(X_train, y_train)
로지스틱 회귀 모델 규제
LogisticRegression 모델의 하이퍼파라미터 penalty 와 C 를 이용하여 규제와 규제의 강도를 지정한다.
penalty:l1벌점 (라쏘 회귀),l2벌점(릿지 회귀),elasticnet(엘라스틱 넷) 방식 중 하나 선택하며, 기본값은l2벌점이다. 즉, 릿지 회귀를 기본 회귀 모델로 사용한다.C:solver로 지정되는 알고리즘에 따라 릿지 회귀 또는 라쏘 회귀 모델에 사용되는 \(\alpha\) 값의 역수에 해당한다. 따라서 0에 가까울 수록 강한 규제를 의미한다. 기본값은 1이다.
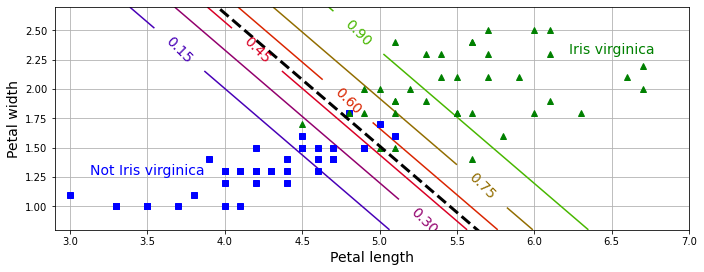
아래 그림의 검정 파선은 꽃잎의 너비와 길이 두 속성을 이용했을 때 버지니카 품종의 여부를 결정하는 결정 경계를 나타낸다. 반면에 다양한 색상의 직선은 버지니카 품종일 가능성(확률)을 보여주는 영역을 구분한다.
4.7. 소프트맥스 회귀#
로지스틱 회귀 모델을 일반화하여 다중 클래스 분류를 지원하도록 만든 모델이 소프트맥스 회귀Softmax regression다. 즉, 소프트맥스 회귀는 3보다 같거나 큰 \(K\)개의 범주로 분류하는 모델이다.
소프트맥스 회귀 모델은 \(K\) 개의 범주 각각에 대해 주어진 데이터 샘플이 해당 클래스에 포함될 확률을 계산한 다음에 가장 큰 확률값을 갖는 범주를 최종 예측값으로 지정한다.
주어진 데이터 샘플에 특정 범주에 속할 확률은 소프트맥스 점수를 이용하여 계산된다.
소프트맥스 점수
데이터 샘플 \(\mathbf x = [x_1, \dots, x_n]\)가 주어졌을 때 \(k\)-범주에 대한 소프트맥스 점수 \(s_k(\mathbf x)\) 는 선형 회귀 방식으로 계산한다.
위 식에서 \(\theta_i^{(k)}\) 는 \(k\)-범주에 대한 소프트맥스 점수를 선형 회귀 방식으로 계산하기 위해 필요한 \(i\) 번째 특성에 대한 가중치 파라미터를 가리킨다. 따라서 \(K\) 개의 클래스로 분류하는 소프트맥스 회귀는 총 \(K \cdot (n+1)\) 개의 파라미터를 학습시켜야 하며 그만큼 훈련시간이 오래 걸린다.
소프트맥스 함수
소프트맥스 함수는 \(K\) 개의 범주 각각에 대해 계산된 소프트맥스 점수를 통합하여 각각의 범주에 포함될 확률을 계산한다. 이때 계산된 \(K\) 개의 확률의 합은 1이 된다.
소프트맥스 함수는 결국 계산된 \(K\) 개의 소프트맥스 점수를 \(K\) 개의 상대적 확률값으로 변환한다. 즉, 하나의 범주에 속할 확률을 계산할 때 타 범주에 대한 소프트맥스 점수도 함께 고려고 모든 확률값의 합은 1이되도록 한다.
앞서 계산된 \(K\) 개의 소프트맥스 점수를 이용하여 해당 샘플이 \(k\)-번째 범주에 속할 확률 \(\hat p_k\)는 다음과 같이 계산된다.
소프트맥스 회귀 모델의 예측 레이블
소프트맥스 회귀 모델의 각 샘플에 대한 최종 예측 레이블 \(\hat y\)는 확률값 \(p_k\)가 최댓값이 되는 \(k\)로 지정된다. 즉, 다음이 성립해야 한다.
소프트맥스 회귀의 비용 함수
\(k\)-범주 각각에 대한 적절한 가중치들의 벡터 \(\mathbf{\theta}^{(k)} = [\theta_0^{(k)}, \theta_1^{(k)}, \dots, \theta_n^{(k)}]\)를 경사하강법을 이용하여 업데이트 한다. 이를 위해 크로스 엔트로피cross entropy를 비용 함수로 사용한다.
위 식에 사용된 기호의 의미는 다음과 같다.
기호 |
의미 |
|---|---|
\(y^{(i)}_k\) |
\(i\)-번째 입력 샘플이 \(k\)-번째 범주에 포함되면 1, 아니면 0. |
\(\hat{p}_k^{(i)}\) |
\(i\)-번째 입력 샘플이 \(k\)-번째 범주에 속할 확률 예측값 |
\(\Theta\) |
\(\mathbf{\theta}^{(1)}, \dots, \mathbf{\theta}^{(K)}\)로 구성된 파라미터 행렬 |
크로스 엔트로피 손실 함수 이해
틀린 예측을 하면 크로스 엔트로피가 매우 커진다. 예를 들어 하나의 샘플에 대한 손실값은 다음과 같다.
예를 들어 해당 샘플의 라벨이 \(k\)라 하자. 그러면 \(y_k=1\)이고 다른 \(y_i\)는 모두 0이기에 손실값은 다음과 같이 매우 단순해진다.
그런데 모델의 예측값이 \(k\)가 아니면 \(\hat p_k\)가 0.5보다 작고 많은 경우 0에 많이 가까워지고 이는 손실값 \(-\log ( \hat{p}_k)\) 가 매우 커질 수 있음을 의미한다.
로그 손실과 크로스 엔트로피
\(K=2\)이면 다음이 성립한다.
이유는 1-번째 범주에 포함되지 않으면 반드시 2-번째 포함됨을 의미하고, 따라서 2-번째 범주에 포함될 확률이 바로 1에서 1-번째 범주에 들어갈 확률을 뺀 값이기 때문이다.
결국 \(K=2\)일 때 크로스 엔트로피 비용함수는 이진 분류 모델인 로지스틱 회귀의 로그 손실 함수와 정확하게 일치한다.
크로스 엔트로피
크로스 엔트로피는 주어진 샘플의 타깃 클래스를 제대로 예측하지 못하는 경우 높은 값을 갖는다. 크로스 엔트로피 개념은 정보 이론에서 유래하며, 자세한 설명은 오렐리앙 제롱의 동영상 “A Short Introduction to Entropy, Cross-Entropy and KL-Divergence”를 참고한다.
붓꽃 데이터 다중 클래스 분류
사이킷런의 LogisticRegression 예측기를 활용한다.
기본값 solver=lbfgs 사용하면 모델이 알아서 다중 클래스 분류를 훈련한다.
아래 코드는 꽃잎의 길이와 너비 두 특성을 이용하여
세토사, 버시컬러, 버지니카 클래스 중 하나를 선택하는 모델을 훈련시킨다.
X = iris.data[["petal length (cm)", "petal width (cm)"]].values
y = iris["target"]
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
softmax_reg = LogisticRegression(C=30, random_state=42) # 조금 약한 alpha 규제
softmax_reg.fit(X_train, y_train)
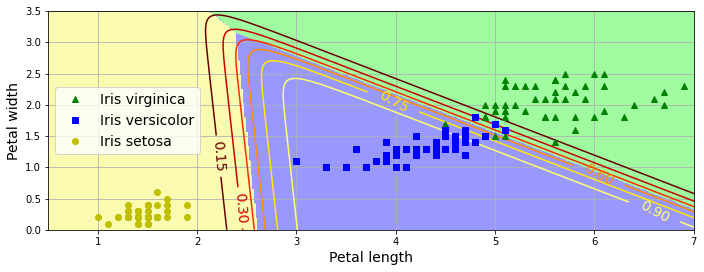
아래 그림은 붓꽃 꽃잎의 너비와 길이를 기준으로 세 개의 품종을 색까로 구분하는 결정 경계를 보여준다. 다양한 색상의 곡선은 버시컬러 품종에 속할 확률의 영역 구분하는 등고선이다.
4.8. 연습문제#
참고: (실습) 모델 훈련 와 (실습) 머신러닝 모델 웹앱
