2. 머신러닝 프로젝트 처음부터 끝까지#
감사의 글
자료를 공개한 저자 오렐리앙 제롱과 강의자료를 지원한 한빛아카데미에게 진심어린 감사를 전합니다.
소스코드
본문에 소개된 코드는 (구글코랩) 머신러닝 프로젝트 처음부터 끝까지에서 직접 실행할 수 있다.
주요 내용
주택 가격을 예측하는 다양한 회귀 모델regression model의 훈련 과정을 이용하여 머신러닝 시스템의 전체 훈련 과정을 살펴본다.

특히 데이터 정제 및 전처리 과정으로 구성된 데이터 준비를 상세히 소개한다.
슬라이드
본문 내용을 요약한 슬라이드 1부, 슬라이드 2부, 슬라이드 3부를 다운로드할 수 있다.
2.1. 머신러닝과 데이터#
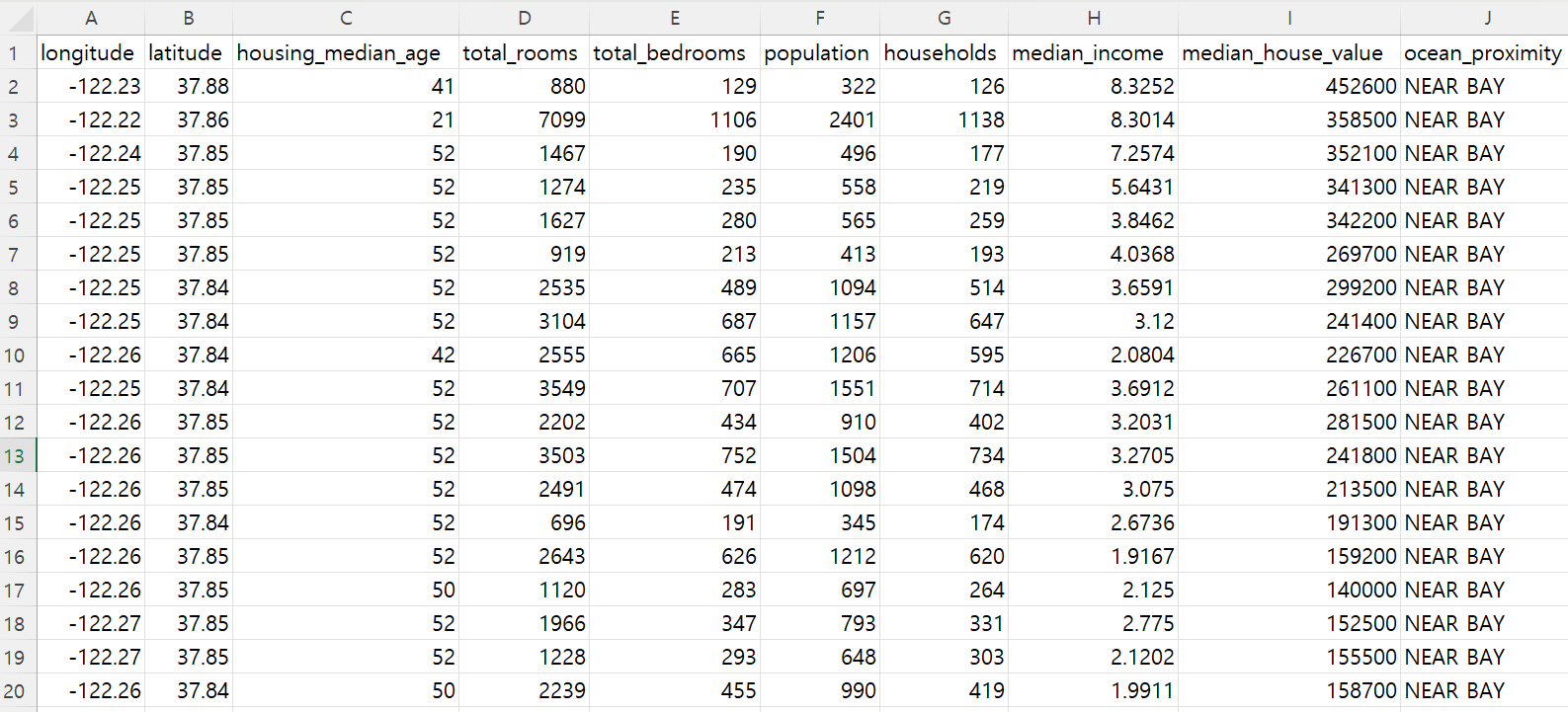
머신러닝으로 문제를 해결하려면 먼저 관련된 데이터를 구하고 기초적인 정보를 확인한 후에 어떤 모델을 어떻게 훈련시킬 것인가를 판단한다. 여기서는 1990년 미국 캘리포니아 주에서 수집한 주택가격 데이터를 사용하며, 아래 그림은 원본 csv 파일의 일부 내용을 보여준다.
2.2. 데이터 활용법 확인#
2.2.1. 데이터 기초 정보 확인#
데이터셋 크기와 특성
1990년도에 시행된 미국 캘리포니아 주의 20,640개 구역별 주택가격 데이터는 위 엑셀 파일 그림의 1번 행에 표시된 대로 경도, 위도, 주택 건물 중위연령, 총 방 수, 총 침실 수, 인구, 가구 수, 중위소득, 주택 중위가격, 해안 근접도 등 총 10개의 특성feature을 포함한다. 참고로 통계 분야에서는 특성을 변수 또는 변인 등으로 부르지만 머신러닝 분야에서는 특성이라 부르는 게 일반적이다.
머신러닝 모델의 타깃
10개의 특성 중에서 주택 중위가격이 부동산과 관련해서 매우 중요하다. 따라서 어떤 구역에 대해 주택 중위가격을 제외한 9개의 특성이 주어졌을 때 해당 구역의 주택 중위가격을 타깃target으로 예측하는 시스템을 머신러닝 모델로 구현하고자 한다.
2.2.2. 훈련 모델 확인#
구역별 주택 중위가격을 타깃으로 예측하는 시스템에 활용될 회귀 모델을 훈련시키고자 한다. 훈련시킬 모델의 특성은 다음과 같다.
지도 학습: 구역별 주택 중위가격을 타깃, 즉 최대한 정확하게 예측해야 하는 목표로 지정한다.
회귀: 주택 중위가격, 즉 이산형 값이 아닌 연속형 값을 예측한다. 보다 세분화하면 다중 회귀이자 단변량 회귀 모델이다.
다중 회귀multiple regression: 구역별로 여러 특성을 주택 가격 예측에 사용
단변량 회귀univariate regression: 구역별로 한 종류의 값만 예측
배치 학습: 빠르게 변하는 데이터에 적응할 필요가 없으며, 데이터셋의 크기도 충분히 작기에 데이터셋 전체를 대상으로 훈련을 진행한다.
이산형 데이터 vs 연속형 데이터
이산형 데이터descrete values는 1, 2, 3, 등 값과 값 사이를 명확하게 구분할 수 있는 데이터을 가리킨다. 반면에 연속형 데이터continuous values은 유리수, 실수 처럼 두 개의 값 사이에 항상 새로운 값이 존재하는 데이터이다.
2.3. 데이터 구하기#
캘리포니아 주택가격 데이터는 매우 유명하여 많은 공개 저장소에서 다운로드할 수 있다. 여기서는 개인 깃허브 리포지토리에 압축파일로 저장한 파일을 다운로드해서 사용한다.
아래 코드의 load_housing_data() 함수는
지정된 깃허브 리포지토리에 저장되어 있는
캘리포니아 주택가격 데이터를 다운로드한 후에
Pandas 데이터프레임으로 변환하여 반환한다.
따라서 housing 변수는 캘리포니아 주택가격 데이터를 담고 있는 데이터프레임을 가리킨다.
housing = load_housing_data()
2.4. 데이터 탐색과 시각화#
데이터 탐색은 훈련을 시작하기 전에 주어진 데이터셋의 다양한 특성을 대략적으로 살펴보는 과정이다. 데이터 시각화는 데이터 탐색을 위한 주요 기법 중의 하나이다. 먼저 데이터프레임의 메서드를 활용한 데이터 탐색을 알아본다.
2.4.1. 데이터프레임과 데이터 탐색#
Pandas의 데이터프레임으로 적재된 데이터셋의 기본적인 데이터 구조를 다양한 메서드를 이용하여 훑어본다.
head() 메서드
데이터프레임에 포함된 처음 5개 샘플을 보여준다.
housing.head()

info() 메서드
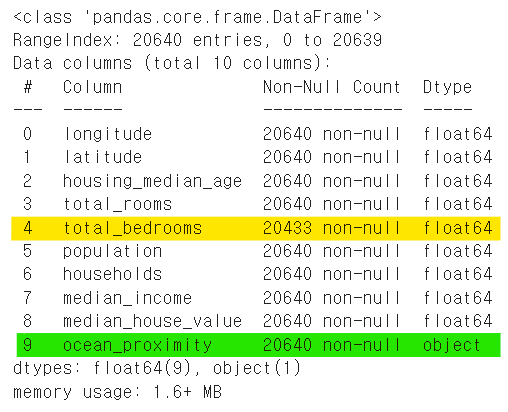
데이터셋의 정보를 요약해서 보여준다.
구역 수: 20,640개.
구역별로 경도, 위도, 주택 건물 중위연령, 해안 근접도 등 총 10개의 조사 항목.
해안 근접도를 뜻하는
ocean_proximity특성은 범주형categorical이고 나머지는 수치형numerical 특성임.특성의
Dtype이object: 범주형 데이터특성의
Dtype이float64: 수치형 데이터
총 방 수를 뜻하는
total_bedrooms특성은 207개의 null 값, 즉 결측치 포함.
housing.info()
범주형 특성 탐색: valule_counts() 메서드
‘해안 근접도’는 5개의 범주로 구분된다.
valule_counts() 메서드는 사용된 특성값과 각각의 특성값이 사용된 횟수를 확인해준다.
housing["ocean_proximity"].value_counts()

각 특성값의 의미는 다음과 같다.
특성값 |
설명 |
|---|---|
<1H OCEAN |
해안에서 1시간 이내 |
INLAND |
내륙 |
NEAR OCEAN |
해안 근처 |
NEAR BAY |
샌프란시스코의 Bay Area 구역 |
ISLAND |
섬 |
수치형 특성 탐색
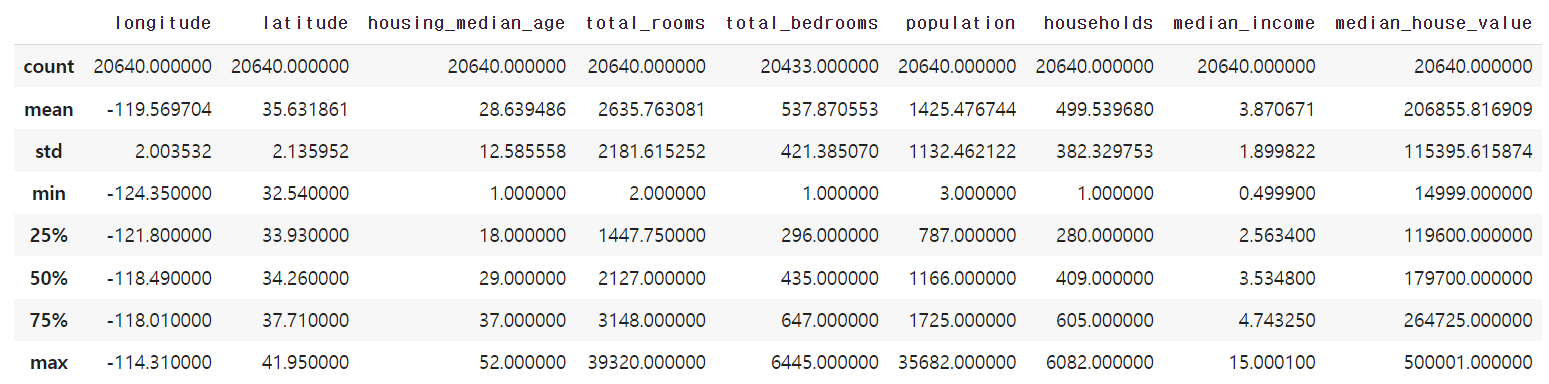
describe() 메서드는 평균값, 표준편차, 사분범위 등 수치형 특성들의 정보를 요약해서 보여준다.
housing.describe()
수치형 특성별 히스토그램
hist() 메서드가 수치형 특성별로 히스토그램을 그린다.
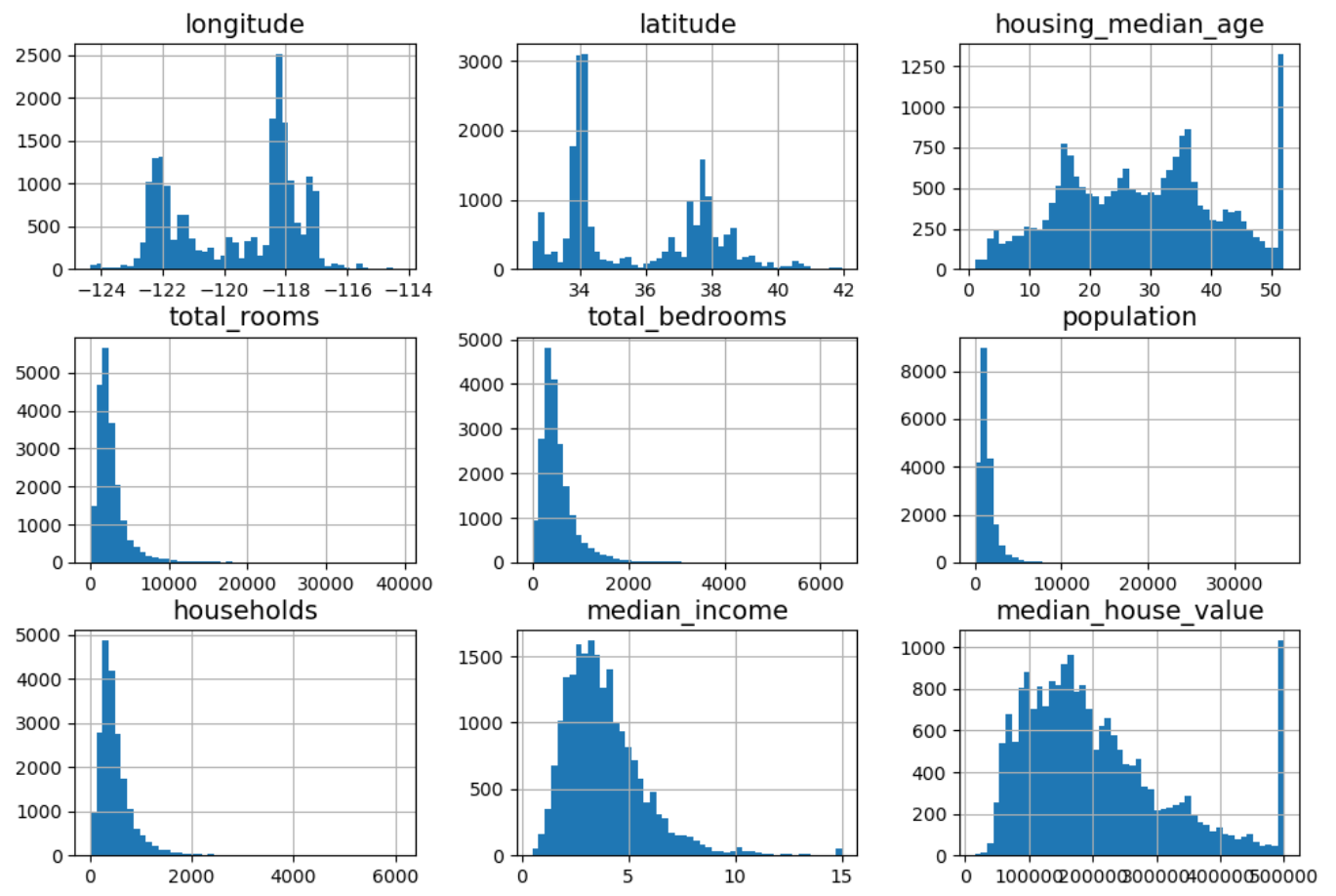
아래 9개의 히스토그램으로부터 다음 정보를 얻을 수 있다.
각 특성마다 사용되는 단위와 스케일이 다르다. 1 단위부터 만 단위까지 다양하다.
일부 특성은 한쪽으로 치우쳐저 있다. 예를 들어
total_rooms,total_bedrooms,population,households등의 특성값들이 오른쪽 꼬리를 길게 갖는다.일부 특성은 값을 제한한 것으로 보인다. 예를 들어
housing_median_age,median_house_value등의 특성값 상한값이 임의로 지정되어 잘린 것처럼 보인다.
housing.hist(bins=50, figsize=(12, 8))
2.4.2. 훈련셋과 테스트셋#
모델 훈련을 시작하기 전에 준비된 데이터셋을 보통 훈련셋training set과 테스트셋test set으로 나눈다. 테스트셋은 훈련 과정중에 전혀 사용되지 않으며 보통 전체 데이터셋의 최대 20% 정도로 선택하며, 전체 데이터셋의 크기에 따라 테스트셋의 크기가 너무 크지 않게 비율을 적절히 조절한다. 훈련셋의 일부는 훈련 중에 훈련의 진척 정도를 측정하는 검증valdation 용도로 활용되며, 아래에서 소개하는 교차 검증에서 유용하게 사용된다.

데이터셋을 훈련셋과 데이터셋으로 나눌 때 보통 계층 샘플링을 사용한다.
계층 샘플링
각 계층별로 적절한 양의 샘플을 추출하는 기법이 계층 샘플링stratified sampling이다. 계층은 유사한 성질의 데이터로 구성된 그룹이며, 계층 샘플링을 사용해야 하는 이유는 계층별로 충분한 양의 샘플이 훈련셋으로 추출되어야 훈련 과정에서 편향이 발생하지 않기 때문이다. 예를 들어, 특정 소득 구간에 포함된 샘플이 과하게 적거나 과하게 많으면 해당 계층의 중요도가 과소 혹은 과대 평가되어 데이터의 실제 특성과 차이(편향)를 보일 수 있다.
캘리포니아 주택가격 데이터셋을 훈련셋과 테스트셋으로 나눌 때 중위소득 특성을 계층 샘플링의 기준으로 삼는다. 이유는 여기서 훈련시키고자 하는 모델이 구역별 주택 중위가격을 예측하는 모델인데 아무래도 중위 주택가격이 구역에 사는 가구의 중위소득과 밀접하게 연관되어 있을 것이기 때문이다.
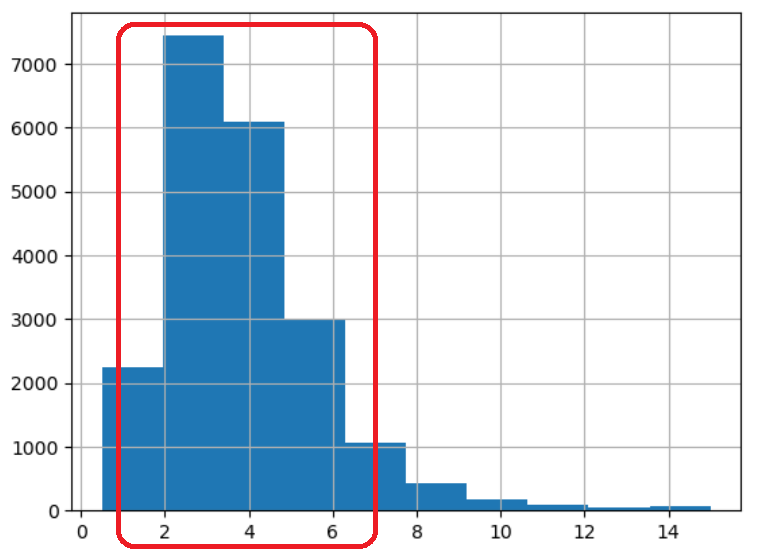
먼저 구역별 중위소득 특성을 대상으로 히스토그램을 그려보면
대부분 구역의 중위소득이 1.5 ~ 6.0, 즉 15,000에서 60,000 달러 사이인 것을 알 수 있다.
hist() 메서드를 특성에 대해 적용하면 하나의 히스토그램을 그린다.
housing['median_income'].hist()
따라서 중위소득 구간을 아래처럼 5개로 구분한 다음에 계층 샘플링을 이용하여 훈련셋과 테스트셋을 구분하면 좋을 것 같아 보인다.
구간 |
범위 |
|---|---|
1 |
0.0 ~ 1.5 |
2 |
1.5 ~ 3.0 |
3 |
3.0 ~ 4.5 |
4 |
4.5 ~ 6.0 |
5 |
6.0 ~ |
먼저 언급된 5 개의 구간으로 구분하는 "income_cat" 특성을 추가한다.
pd.cut() 함수는 특성과 구간 구분이 주어지면 각 구간에 해당하는 특성값들에 지정된 레이블을 할당하는
형식으로 새로운 특성값들을 만들어 낸다.
housing["income_cat"] = pd.cut(housing["median_income"],
bins=[0., 1.5, 3.0, 4.5, 6., np.inf],
labels=[1, 2, 3, 4, 5])
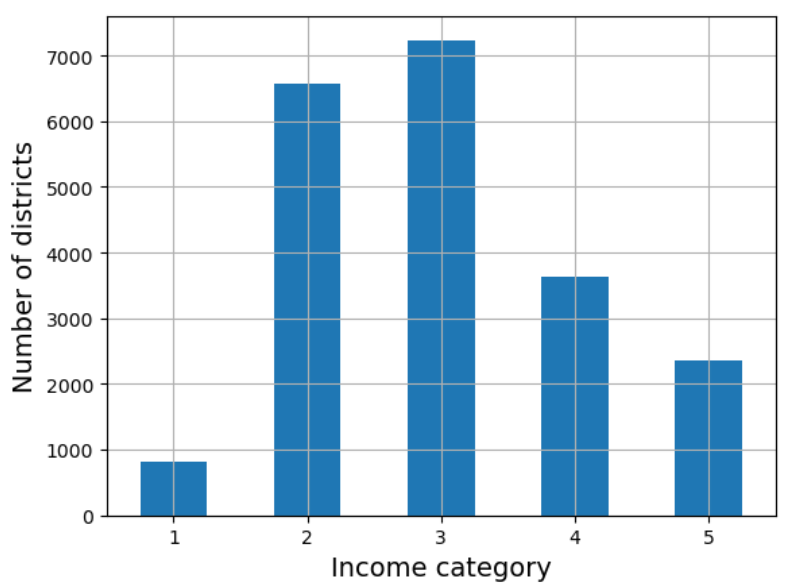
income_cat 특성에 따른 데이터 분포는 다음과 같다.
housing["income_cat"].value_counts().sort_index().plot.bar(rot=0, grid=True)
plt.xlabel("Income category")
plt.ylabel("Number of districts")
이제 "income_cat" 특성에 사용된 값들의 분포 비율을 반영하면서
훈련셋과 테스트셋을 8대 2로 나눈다.
사이킷런의 train_test_split() 함수는 데이터프레임에 속한 샘플을
지정된 비율로 두 개의 데이터프레임으로 나눌 때
계층 샘플링을 지원한다.
from sklearn.model_selection import train_test_split
strat_train_set, strat_test_set = train_test_split(housing,
test_size=0.2,
stratify=housing["income_cat"],
random_state=42)
계층 샘플링이 무작위 샘플링보다 계층별 샘플의 비율을 훨씬 잘 유지함을 아래 표가 확인해준다.
소득 구간 |
전체(%) |
계층 샘플링(%) |
무작위 샘플링(%) |
|---|---|---|---|
1 |
3.98 |
4.00 |
4.24 |
2 |
31.88 |
31.88 |
30.74 |
3 |
35.06 |
35.05 |
34.52 |
4 |
17.63 |
17.64 |
18.41 |
5 |
11.44 |
11.43 |
12.09 |
2.4.3. 데이터 시각화#
데이터 시각화는 지금까지와는 달리 훈련셋만을 대상으로 진행한다.
아래 코드는 housing 변수가 가리키는 데이터프레임을 전체 데이터셋에서
계층 샘플링을 이용하여 생성된 훈련셋의 복사본으로 변경한다.
housing = strat_train_set.copy()
지리적 데이터 시각화
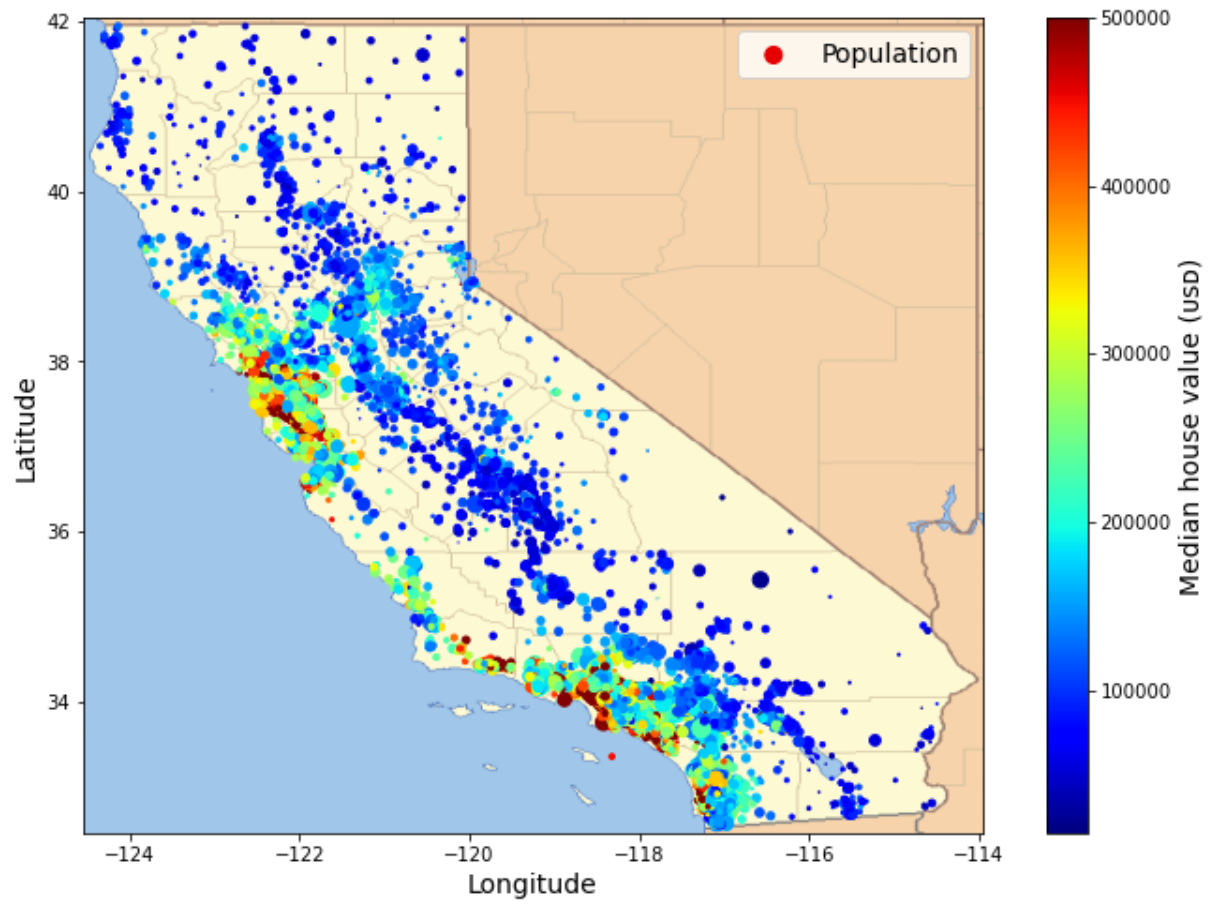
데이터의 지리적 분포를 시각화한다. 즉, 경도와 위도 정보를 이용하여 구역 정보를 산포도로 나타내면 인구의 밀집 정도를 확인할 수 있다. 예를 들어, 샌프란시스코의 Bay Area, LA, 샌디에고 등 유명 대도시의 특정 구역이 높은 인구 밀도를 갖는다.
데이터프레임의 plot() 메서드는 다양한 종류의 그래프를 그린다.
kind 매개변수의 키워드 인자를 "scatter"로 지정하면 산점도를 그린다.
이외에 다양한 키워드 인자를 그래프 옵션으로 지정할 수 있다.
예를 들어 구역의 주택 중위가격을 색상으로,
인구밀도는 원의 크기로 활용하면
인구 밀도가 높은 유명 대도시의 특정 구역에 위치한
주택 가격이 높다는 일반적인 사실 또한 쉽게 확인된다.
housing.plot(kind="scatter",
x="longitude",
y="latitude",
grid=True,
s=housing["population"] / 100,
label="population",
c="median_house_value",
cmap="jet",
colorbar=True,
legend=True,
figsize=(10, 7))
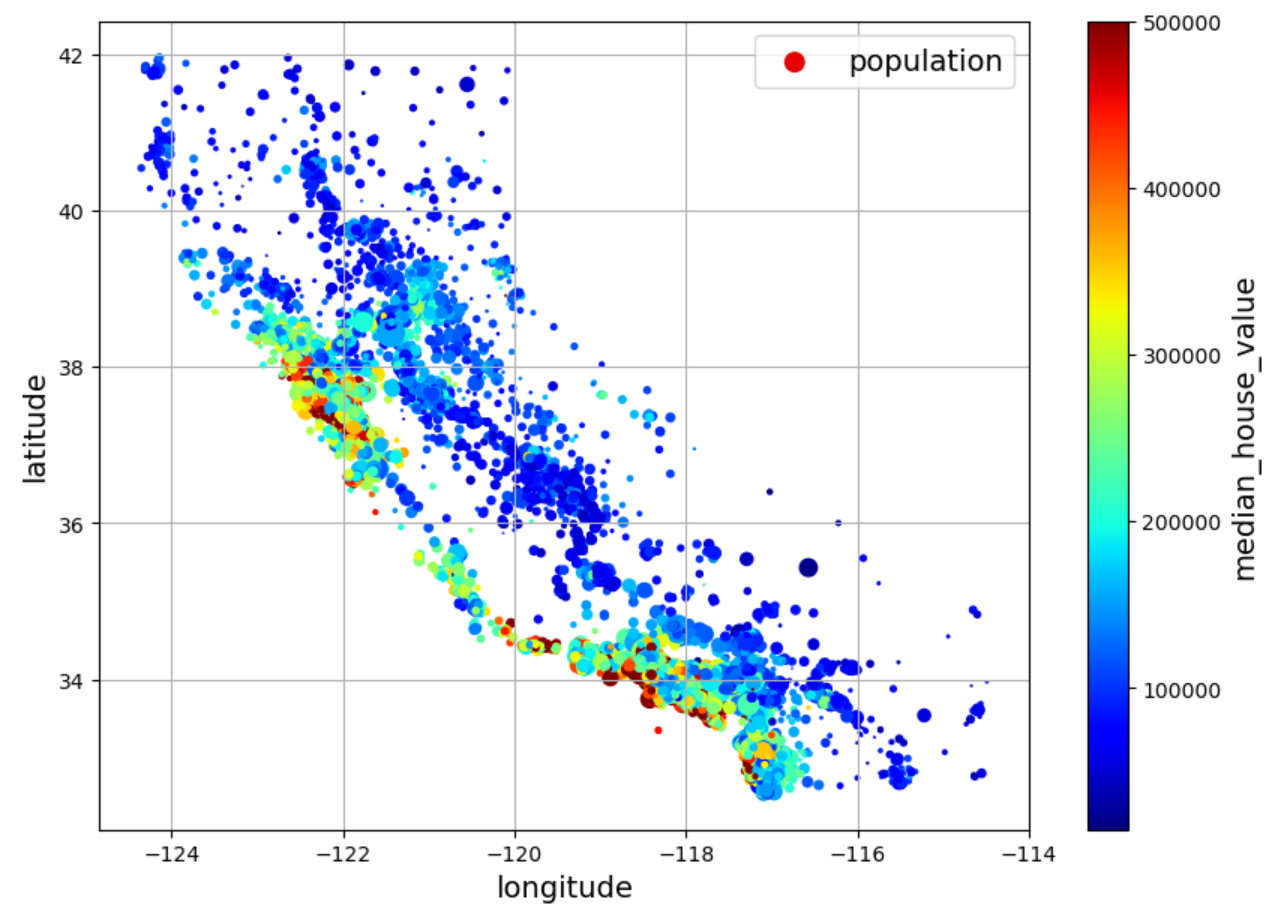
아래 그림은 산점도와 캘리포니아 주의 실제 지도를 합친 결과이다.
상관관계
데이터프레임의 corr() 메서드는 수치형 특성들 사이의 선형 상관계수를 계산한다.
corr_matrix = housing.corr()
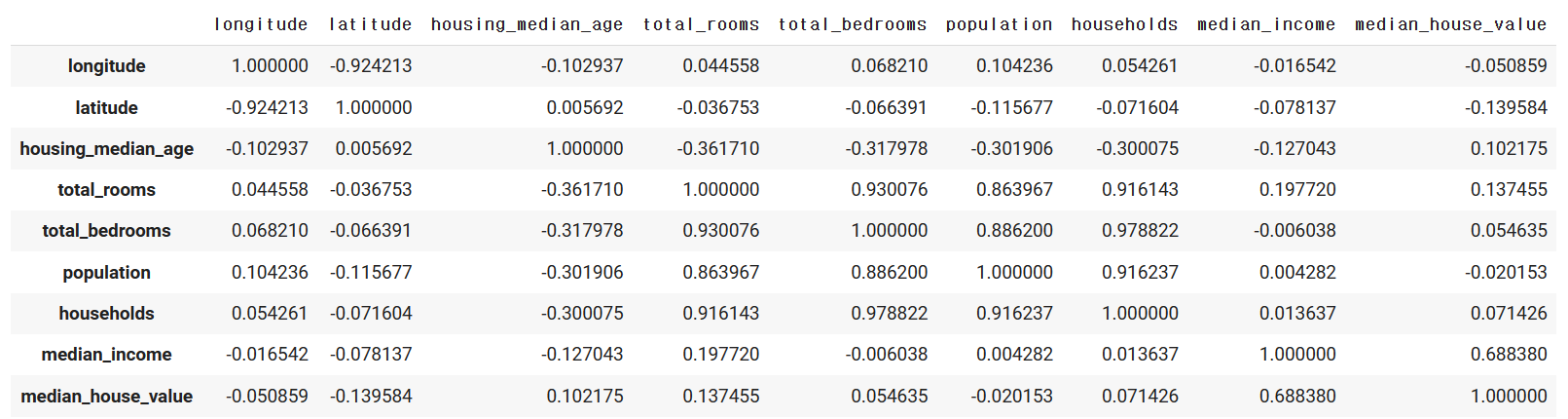
주택 중위가격 특성과 다른 특성 사이의 선형 상관관계를 나타내는 상관계수는 다음과 같다.
corr_matrix["median_house_value"].sort_values(ascending=False)

상관계수는 -1에서 1 사이의 값으로 표현된다.
상관계수 |
선형 상관관계 |
|---|---|
1에 가까울 수록 |
강한 양의 선형 상관관계 |
-1에 가까울 수록 |
강한 음의 선형 상관관계 |
0에 가까울 수록 |
매 약한 선형 상관관계 |
상관계수와 상관관계
상관계수가 0이라는 것은 선형 상관관계가 없다는 의미이지 서로 아무런 상관관계가 없다는 말이 아니다. 또한 선형계수가 1이라 하더라도 두 특성이 변하는 비율이 반드시 1대 1은 아니다. 예를 들어 하나의 특성값이 1 커질 때 다른 특성값이 0.0001씩 변해도 선형계수는 1이다. 즉, 하나의 특성값이 커질 때 다른 특성값이 일정하게 변하면 선형계수는 1이 된다.
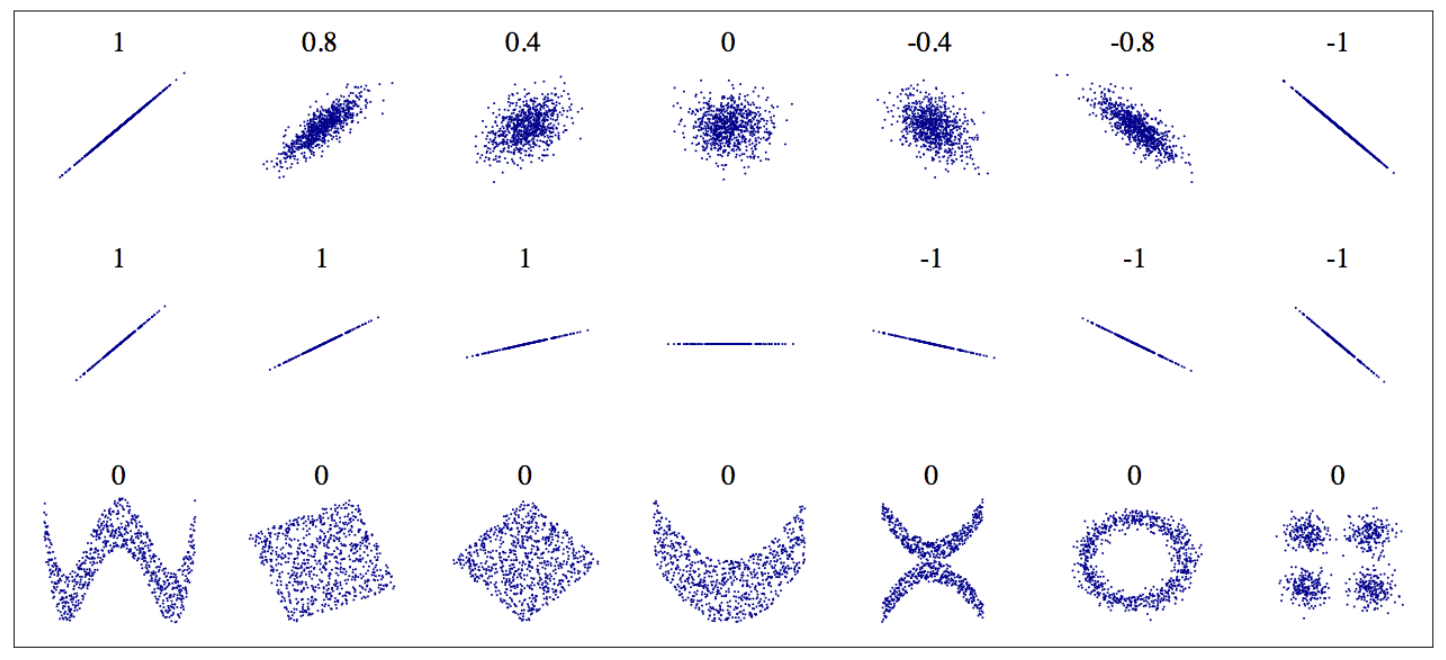
<그림 출처: 위키백과>
주택 중위가격과 중위소득의 상관계수가 0.68로 가장 높다. 이는 중위소득이 올라가면 주택 중위가격도 상승하는 경향이 나름 강하게 있음을 의미한다. 하지만 아래 산점도의 점들이 너무 넓게 퍼져 있어서 완벽한 선형관계와는 거리가 멀다.
housing.plot(kind="scatter", x="median_income", y="median_house_value", alpha=0.1, grid=True)
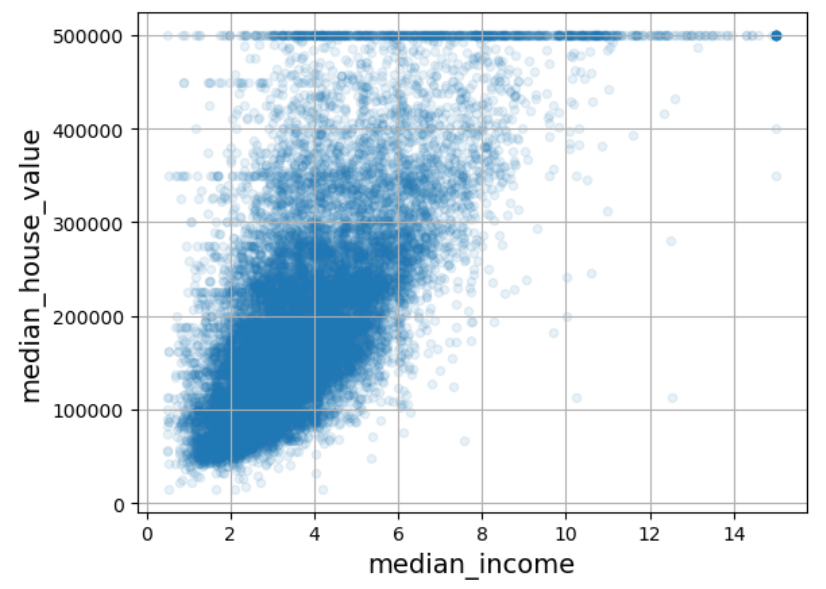
50만 달러에서 보이는 수평선은 50만 달러 이상은 모두 50만달러로 지정한 결과로 보여진다. 그렇게 인위적으로 조작된 데이터는 모델 훈련에 도움이 되지 않아 제거하는 것이 일반적으로 좋지만 여기서는 그대로 두고 사용한다.
경우에 따라 기존의 특성을 조합해서 새로운 특성을 활용할 수도 있다. 예를 들어 구역별 총 방 수와 총 침실 수 대신 아래 특성이 보다 유용해 보인다.
침실 비율(
bedrooms_ratio)가구당 방 수(
rooms_per_house)가구당 평균 가구원수(
people_per_house)
실제로 세 특성을 새로 추가한 다음에 상관계수를 확인하면 침실 비율과 주택 중위가격 사이의 선형 상관관계가 중위소득을 제외한 기존의 다른 특성들에 비해 높게 나타난다.
2.5. 데이터 준비: 정제와 전처리#
데이터 탐색을 통해 확인한 지도학습 회귀 모델을 훈련시키기 위해 먼저 적절한 훈련용 데이터를 준비해야 한다. 데이터 준비는 데이터 정제와 데이터 전처리 과정으로 이뤄진다.
데이터 정제
일반적으로 결측치 처리, 이상치와 노이즈 제거를 의미한다.
캘리포니아 주택가격 데이터셋은 구역별 총 방 수를 의미하는 total_rooms 특성에서
결측치가 일부 포함되어 있지만 이상치 또는 노이즈는 포함하지 않는다.
데이터 전처리
수치형 특성과 범주형 특성을 구분하여 수행한다. 캘리포니아 주택가격 데이터셋에 대한 전처리로 다음을 수행한다.
범주형 특성 전처리: 원-핫-인코딩
수치형 특성 전처리: 특성 스케일링과 특성 조합
캘리포니아 주택가격 데이터셋의 특성에 대해 다음 전처리를 진행하려 한다.
비율 특성 추가
침실 비율 특성
가구당 방 수 특성
가구당 평균 가구원수 특성
로그 변환:
"total_bedrooms","total_rooms","population","households","median_income"구역 군집 특성 추가: 위도와 경도, 주택 중위가격 정보를 활용하여 유사한 구역끼리 구성된 군집으로 분류
해안 근접도 특성에 대한 원-핫-인코딩 적용: 5개의 범주로 구분된 특성을 총 5개의 특성으로 구성된 수치형 데이터로 변환
데이터 준비 자동화
데이터 정제와 전처리 전과정을 사이킷런 라이브러리에서 제공하는 API를 활용한다. 먼저 사이킷런 API의 기본 특성을 살펴본 다음에 앞서 언급된 정제와 전처리 내용을 처리하는 각각의 API를 하나씩 살펴본다. 그런 다음 사이킷런 API를 연동하여 정제와 전처리 전 과정을 한꺼번에 순차적으로 처리하는 파이프라인pipeline으로 구성하여 자동화는 방식까지 소개한다.
API란?
API는 영어로 Application Programming Interface, 즉 응용 프로그래밍 인터페이스의 줄임말이다. 간단하게 말해 API는 응용 프로그램을 가리킨다. 프로그래밍 분야에서는 함수, 클래스, 모듈 등 프로그램 구현에 유용한 도구를 총칭하는 용어로, 특히 여기서는 사이킷런 라이브러리에 포함된 클래스, 메서드, 함수를 가리키는 용어로 사용된다.
2.5.1. 사이킷런 API#
사이킷런의 API는 일반적으로 다음 세 클래스의 인스턴스로 생성된다.
추정기estimator
fit()메서드를 지원하는 클래스의 인스턴스일반적으로 변환기와 예측기 둘 중의 하나임.
변환기transformer
fit()메서드와transform()메서드를 함께 지원하는 클래스의 인스턴스일반적으로 데이터 정제와 전처리 과정에서 주로 사용됨.
fit()메서드: 데이터 변환에 필요한 정보 계산transform()메서드: 데이터 변환 실행fit_transform()메서드도 함께 지원:fit()메서드와transform()메서드를 연속으로 호출.
예측기predictor
fit()메서드와predict()메서드를 함께 지원하는 클래스의 인스턴스일반적으로 모델이라 불림.
fit()메서드: 모델의 훈련 관장predict()메서드: 모델의 훈련이 종료 된 후 실전에서 예측값을 계산할 활용predict()메서드가 예측한 값의 성능을 측정하는score()메서드도 일반적으로 함께 지원됨.일부 예측기는 예측값의 신뢰도를 평가하는 기능도 함께 제공.
2.5.2. SimpleImputer 변환기: 결측치 처리#
입력 데이터셋의 총 침실 수를 의미하는 total_bedrooms 특성에 168개 구역의 값이 NaN(Not a Number)으로 표시되어 있는데
이는 168개 구역에 대해 총 침실 수 정보가 누락되어 있음을 의미한다.
null_rows_idx = housing.isnull().any(axis=1)
housing.loc[null_rows_idx].head()

머신러닝 모델은 일반적으로 결측치가 있는 데이터셋을 잘 활용하지 못하며, 일반적으로 아래 방법 중 하나를 선택해서 결측치를 없애는 데이터 정제를 실행한다.
방법 1: 해당 구역 샘플 제거
방법 2: 해당 특성 삭제
방법 3: 평균값, 중위수, 최빈값, 0, 또는 주변에 위치한 값 등 특정 값으로 결측치 채우기
여기서는 중위수median로 결측치를 대체하는 방법 3을 적용한다. 아래 코드는 총 방 수 특성의 결측치를 해당 특성의 중위수로 대체한다.
median = housing["total_bedrooms"].median()
housing["total_bedrooms"].fillna(median, inplace=True)
하지만 여기서는 사이킷런의 SimpleImputer 변환기를 이용하여 모든 결측치를 중위수median로
대체하는 방법을 사용한다.
이유는 이어서 소개하는 사이킷런에서 제공하는 다른 용도의 데이터 전처리 변환기들과 함께
하나의 변환기 파이프라인을 구성하여 데이터 정제와 전처리를 자동화시킬 수 있기 때문이다.
아래 코드는 SimpleImputer 변화기 객체를 이용하여 결측치를 각 특성의 중위수로 채운다.
원래 무든 수치형 특성의 결측치를 대상으로 하지만 캘리포니아주 주택가격 데이터셋에는
총 방 수 특성에만 결측치가 존재하기에 결과는 위 코드와 동일하다.
from sklearn.impute import SimpleImputer
housing_num = housing.select_dtypes(include=[np.number]) # 수치형 특성들만 선택
imputer = SimpleImputer(strategy="median")
imputer.fit(housing_num)
X = imputer.transform(housing_num) # 결과는 np.array 자료형
# 아래 테이블을 보여주기 위해 데이터프레임으로 변환.
housing_tr = pd.DataFrame(X, columns=housing_num.columns, index=housing_num.index)
housing_tr.loc[null_rows_idx].head()
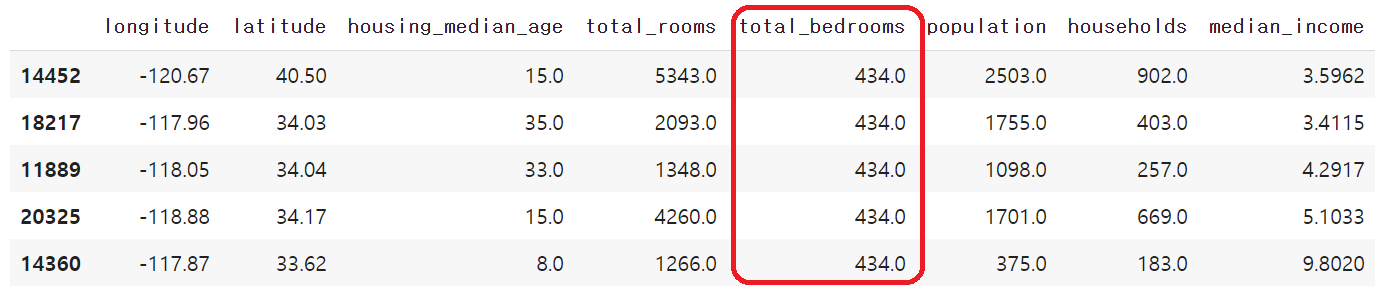
참고: 아래 코드 (1)의 두 줄 코드를 코드 (2)의 한 줄 코드로 대체할 수 있다.
이유는 fit_transform() 메서드는 fit() 메서드와 transform() 메서드를 연속으로 호출하기 때문이다.
코드 (1)
imputer.fit(housing_num) X = imputer.transform(housing_num)
코드 (2)
X = imputer.fit_transform(housing_num)
2.5.3. 입력 데이터셋과 타깃 데이터셋#
부적절한 데이터 샘플을 처리하는 데이터 정제 과정이 끝나면 모델 훈련에 적합한 데이터셋을 준비하는 전처리 과정을 진행한다. 하지만 데이터 전처리를 진행하기 전에 먼저 훈련셋을 다시 입력 데이터셋과 타깃 데이터셋으로 구분한다. 이유는 입력 데이터셋과 타깃 데이터셋에 대한 전처리 과정이 일반적으로 다르기 때문이다. 또한 여기서는 입력 데이터셋에 대해서만 전처리를 실행한다.
타깃 데이터셋은 일반적으로 전처리 대상이 아니지만 경우에 따라 변환이 요구될 수 있다. 예를 들어, 타깃 데이터셋의 두터운 꼬리 분포를 따르는 경우 로그 함수를 적용하여 데이터의 분포가 보다 균형잡히도록 하는 것이 권장된다.
타깃 데이터셋
모델이 훈련을 통해 최대한 정확하계 예측해야 하는 값으로 구성되며, 여기서는 구역별 주택 중위가격을 타깃으로 지정한다. 즉, 앞으로 다룰 모델은 주어진 구역의 주택 중위가격을 최대한 정확하게 예측하도록 훈련된다.
입력 데이터셋
타깃으로 지정된 값을 예측하는 데에 필요한 정보로 구성된 데이터셋이다. 여기서는 구역별 주택 중위가격을 제외한 나머지 특성들로 구성된 데이터셋을 입력 데이터셋으로 사용한다. 따라서 주택 중위가격이 제외된 구역의 다른 정보가 입력되면 해당 구역의 주택 중위가격을 예측하도록 모델이 훈련된다.
입력/타깃 데이터셋 구분
정리하면 다음과 같이 계층 샘플링으로 얻어진 훈련셋 strat_train_set 을
입력 데이터셋 과 타깃 데이터셋으로 구분한다.
입력 데이터셋: 주택 중위가격 특성이 제거된 훈련셋
housing = strat_train_set.drop("median_house_value", axis=1)
타깃 데이터셋: 주택 중위가격 특성으로만 구성된 훈련셋
housing_labels = strat_train_set["median_house_value"].copy()
2.5.4. OneHotEncoder 변환기: 범주형 특성 전처리#
해안 근접도 특성 ocean_proximity는 5 개의 범주를 나타내는 문자열을 값으로 사용한다.
그런데 사이킷런의 머신러닝 모델은 일반적으로 문자열과 같은 텍스트 데이터를 다루지 못한다.
가장 단순한 해결책으로 5 개의 범주를 정수로 변환할 수 있다.
범주 |
숫자 |
|---|---|
<1H OCEAN |
0 |
INLAND |
1 |
ISLAND |
2 |
NEAR BAY |
3 |
NEAR OCEAN |
4 |
하지만 이 방식은 경우에 따라 작은 수보다 큰 수가 좋다라는 의미로 모델 훈련과정에서 잘못 활용될수 있는 위험성을 내포한다. 이유는 해안 근접도의 의미는 여기서는 해안과의 거리를 단순히 구분하기 위한 용도로 사용되기 때문이다. 그리고 해안에 근접한다 해서 주택 가격이 기본적으로 더 비싸지거나 싸지지는 않는다.
범주형 특성을 수치화하는 다른 방식은 원-핫 인코딩one-hot encoding이다. 원-핫 인코딩은 수치화된 범주들 사이의 크기 비교를 피하기 위해 더미dummy 특성을 활용한다.
더미 특성
프로그래밍 분야에서 더미, 영어로 dummy는 의미 없는 값을 의미한다. 여기서 더미 특성은 한 구역의 해안 근접도를 지정할 때 반드시 필요한 값은 아니지만 함께 고려하는 특성을 가리키는 의미로 사용한다.
원-핫 인코딩을 적용하면 해안 근접도 특성을 삭제하고 대신 다섯 개의 범주 전부를 새로운 특성으로 추가한다. 또한 다섯 개의 특성에 사용되는 값은 다음 방식으로 지정된다.
삭제된 카테고리의 특성값: 1
나머지 카테고리의 특성값: 0
예를 들어, INLAND를 해안 근접도 특성값으로 갖던 샘플은
INLAND라는 ocean_proximity 특성 대신에
다음 모양의 특성값을 갖게 된다.
[0.0, 1.0, 0.0, 0.0, 0.0]
리스트에 포함된 다섯 개 각각의 값은 차례대로 다음 특성에 해당하는 값을 가리킨다.
'<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN'
사이킷런의 OneHotEncoder 변환기가 원-핫-인코딩을 지원하며
해안 근접도를 변환한 결과는 다음과 같다.
from sklearn.preprocessing import OneHotEncoder
housing_cat = housing[["ocean_proximity"]]
cat_encoder = OneHotEncoder(sparse_output=False)
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
housing_cat_onehot = pd.DataFrame(housing_cat_1hot,
columns=cat_encoder.get_feature_names_out(),
index=housing_cat.index)
housing_cat_onehot
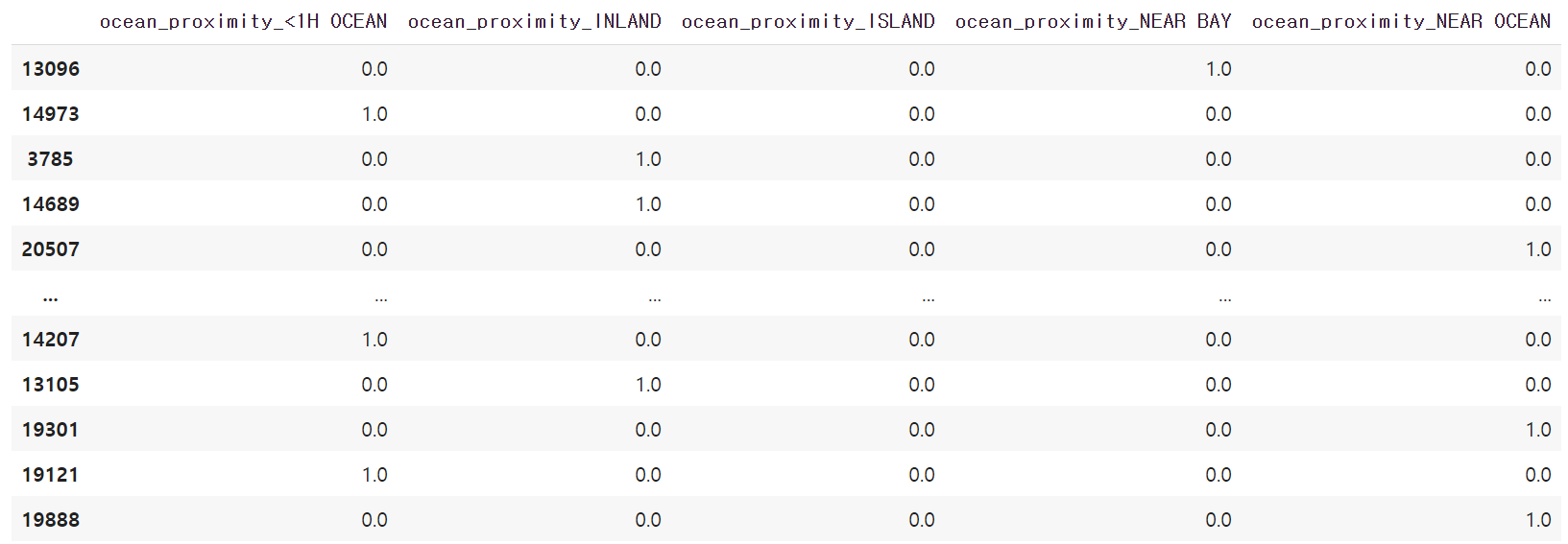
2.5.5. MinMaxScaler와 StandardScaler 변환기: 수치형 특성 스케일링#
머신러닝 알고리즘은 입력 데이터셋의 특성값들의 스케일scale이 비슷할 때 보다 잘 훈련된다. 따라서 모든 특성의 스케일을 통일하는 스케일링scaling 전처리를 일반적으로 실행한다.
스케일링은 보통 아래 두 가지 방식을 사용한다.
min-max 스케일링(정규화)
표준화
정규화: min-max 스케일링
정규화normalization라고 불리는 min-max 스케일링은 아래 식을 이용하여 모든 특성값 \(x\)를 0에서 1 사이의 값으로 변환한다. \(max\) 와 \(min\) 은 각각 해당 특성값들의 최댓값과 최솟값을 가리킨다.
min-max 스케일링은 이상치에 매우 민감하다.
예를 들어 이상치가 매우 크면 분모가 분자에 비해 훨씬 크게 되어 변환된 값이 0 근처에 몰리게 된다.
아래 코드는 사이킷런의 MinMaxScaler 변환기를 모든 수치형 특성에 대해
min-max 스케일링을 실행한다.
from sklearn.preprocessing import MinMaxScaler
min_max_scaler = MinMaxScaler(feature_range=(0, 1))
housing_num_min_max_scaled = min_max_scaler.fit_transform(housing_num)
하지만 여기서는 정규화 보다는 표준화를 이용하여 수치형 특성들에 대해 스케일링을 실행한다.
표준화
표준화standardization는 아래식을 이용하여 특성값 \(x\)를 변환한다. 단, \(\mu\) 와 \(\sigma\) 는 각각 해당 특성값들의 평균값과 표준편차를 가리킨다.
변환된 특성은 평균값은 0, 표준편차는 1인 분포를 따르며, 이상치에 상대적으로 덜 영향을 받는다.
아래 코드는 사이킷런의 StandardScaler 변환기를 이용하여 모든 수치형 특성에 대해 표준화를 실행한다.
from sklearn.preprocessing import StandardScaler
std_scaler = StandardScaler()
housing_num_std_scaled = std_scaler.fit_transform(housing_num)
2.5.6. FunctionTransformer 변환기#
min-max 스케일링을 진행하려면 먼저 각 특성의 최댓값과 최솟값을,
표준화를 진행하려면 먼저 각 특성의 평균값과 표준편차를 알아야 하는데
이를 위해 MinMaxScaler 또는 Standardscaler 클래스의 fit() 메서드를 이용한다.
따라서 위 코드에서처럼 fit_transform() 메서드를 데이터셋에 적용하면
먼저 fit() 메서드가 실행되어 변환에 필요한 값들을 생성하고
이후에 이들을 이용하여 transform() 메서드가 데이터를 변환한다.
그런데 경우에 따라 어떤 정보도 필요 없이 바로 데이터 변환을 진행할 수도 있다.
그리고 이럴 때는 fit() 메서드를 사용할 필요가 없는데,
이런 변환기는 FunctionTransformer 클래스의 인스턴스를 활용하여 간단하게 지정할 수 있다.
여기서는 로그 변환과 비율 계산을 지원하는 두 개의 변환기를
FunctionTransformer 클래스의 인스턴스로 지정해서 활용한다.
로그 변환기
데이터셋이 두터운 꼬리 분포를 따르는 경우,
즉 히스토그램이 지나치게 한쪽으로 편향된 경우
스케일링을 적용하기 전에 먼저
로그 함수를 적용하여 어느 정도 좌우 균형이 잡힌 분포로 변환할 것을 권장한다.
아래 그림은 구역별 인구로 구성된 population 특성값에 로그함수를 적용할 때 분포가 보다 균형잡히는 것을 잘 보여준다.
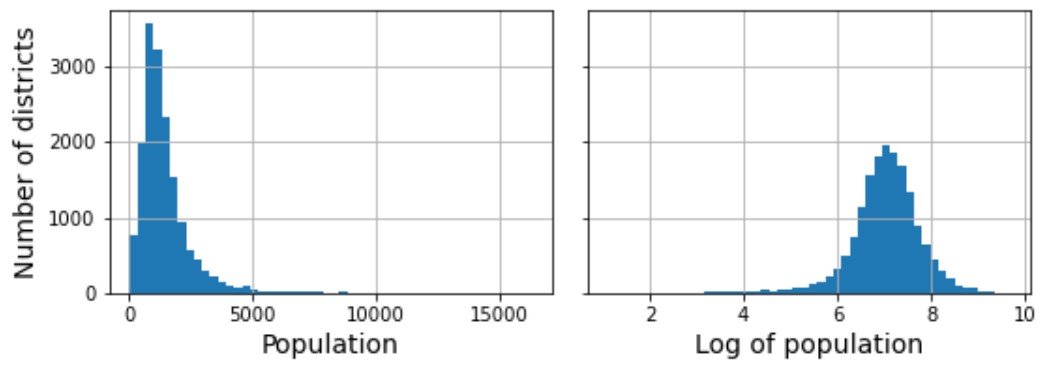
여기서는 로그 변환이 필요한 모든 특성에 대해 아래 형식의 로그 변환기를 적용한다.
FunctionTransformer(np.log)
적용대상 특성은 다음과 같다.
"total_bedrooms", "total_rooms", "population", "households", "median_income"
비율 계산 변환기
두 개의 특성 사이의 비율을 계산하여 새로운 특성을 생성하는 변환기 또한
FunctionTransformer를 활용할 수 있다.
FunctionTransformer(lambda X: X[:, [0]] / X[:, [1]])
비율 계산 변환기를 이용하여 아래 특성을 새롭게 생성할 수 있다.
침실 비율(bedrooms for room):
housing['total_bedrooms'] / housing['total_rooms']가구당 방 수(rooms for household):
housing['total_bedrooms'] / housing['households']가구당 평균 가구원수(population per household):
housing['population'] / housing['households']
2.5.7. 군집 변환기: 사용자 정의 변환기#
데이터 준비 과정에서 경우에 따라 사용자가 직접 변환기를 구현해야할 필요가 있다.
그런데 SimpleImputer 변환기의 경우처럼
먼저 fit() 메서드를 이용하여 평균값, 중위수 등과 같은 정보를 데이터셋으로부터 계산한 다음에
transform() 메서드를 적용할 수 있는 변환기는
직접 클래스로 선언해야 한다.
무엇보다도 사이킷런의 다른 변환기와 호환이 되도록 하기 위해서
fit() 과 transform() 등 다양한 메서드를 모두 직접 구현해야 한다.
여기서는 캘리포니아 주 20,640 개의 구역을 서로 가깝게 위치한 구역들로 묶어 총 10개의 군집cluster으로 구분하는 변환기 클래스를 다음과 같이 선언한다.
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.cluster import KMeans
from sklearn.metrics.pairwise import rbf_kernel
class ClusterSimilarity(BaseEstimator, TransformerMixin):
def __init__(self, n_clusters=10, gamma=1.0, random_state=None):
self.n_clusters = n_clusters
self.gamma = gamma
self.random_state = random_state
def fit(self, X, y=None, sample_weight=None):
self.kmeans_ = KMeans(self.n_clusters, random_state=self.random_state)
self.kmeans_.fit(X, sample_weight=sample_weight)
return self # 항상 self 반환
def transform(self, X):
return rbf_kernel(X, self.kmeans_.cluster_centers_, gamma=self.gamma)
def get_feature_names_out(self, names=None):
return [f"Cluster {i} similarity" for i in range(self.n_clusters)]
cluster_simil = ClusterSimilarity(n_clusters=10, gamma=1., random_state=42)
similarities = cluster_simil.fit_transform(housing[["latitude", "longitude"]],
sample_weight=housing_labels)
위 코드에 대한 설명은 8장 비지도 학습에서 자세히 다룬다. 여기서는 대신 다음 세 가지만을 기억해 두자.
첫째, 변환기를 선언할 때 BaseEstimator와 TransformerMixin 두 개의 클래스를 상속해야 한다.
BaseEstimator클래스 상속: 하이퍼파라미터를 조정을 자동화할 때 필요한get_params(),set_params()두 메서드 상속TransformerMixin클래스 상속:fit_transform()메서드 상속
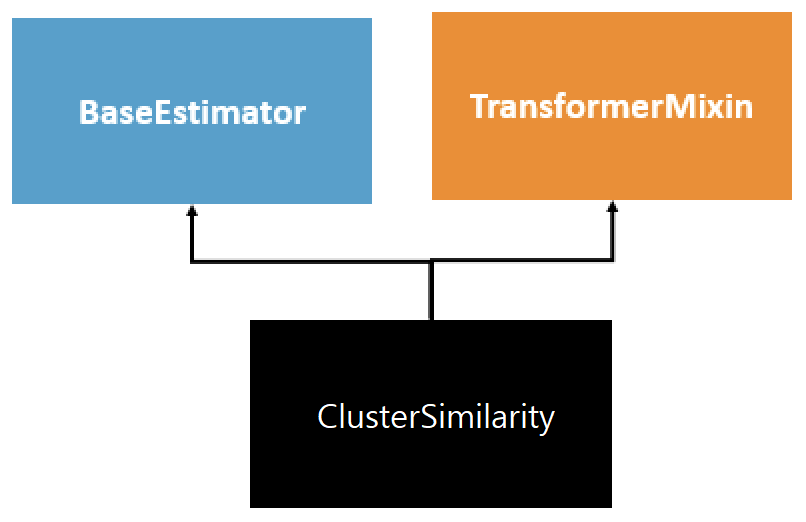
둘째, get_feature_names_out() 메서드를 재정의해서 변환기에 의해 새로 생성된 특성들의 이름을 지정한다.
셋째, ClusterSimilarity 변환기를 이용하여 얻어진 군집 특성을 이용하면 아래 결과를 얻을 수 있다.
모든 구역을 10개의 군집으로 분류한다.
transform()메서드는 각 샘플에 대해 10개의 센트로이드와의 유사도 점수를 계산한다. 유사도는fit()메서드가 알아낸 10개의 센트로이드 정보를 이용한다. 아래코드에서 센트로이드 계산을 위해 사용되는fit()메서드는 위도와 경도 정보뿐만 아니라 해당 구역의 중위소득을 참고한다. 즉, 중위소득이 비슷한 구역들의 거리가 보다 가까워지도록 계산한다.
cluster_simil = ClusterSimilarity(n_clusters=10, gamma=1., random_state=42)
similarities = cluster_simil.fit_transform(housing[["latitude", "longitude"]],
sample_weight=housing['median_income'])
처음 5 개 샘플과 각 센트로이드에 대한 유사도 점수는 다음과 같다. 예를 들어 첫째 샘플의 경우 7번 인덱스의 값이 0.99로 가장 큰데, 이는 첫째 샘플이 8번째 군집의 센트로이드와 가장 유사함을 의미한다.
similarities[:5].round(2)
array([[0. , 0.14, 0. , 0. , 0. , 0.08, 0. , 0.97, 0. , 0.61],
[0.6 , 0. , 0.99, 0. , 0. , 0. , 0.03, 0. , 0.12, 0. ],
[0. , 0.29, 0. , 0. , 0.01, 0.45, 0. , 0.74, 0. , 0.31],
[0.68, 0. , 0.21, 0. , 0. , 0. , 0.52, 0. , 0. , 0. ],
[0.82, 0. , 0.89, 0. , 0. , 0. , 0.13, 0. , 0.03, 0. ]])
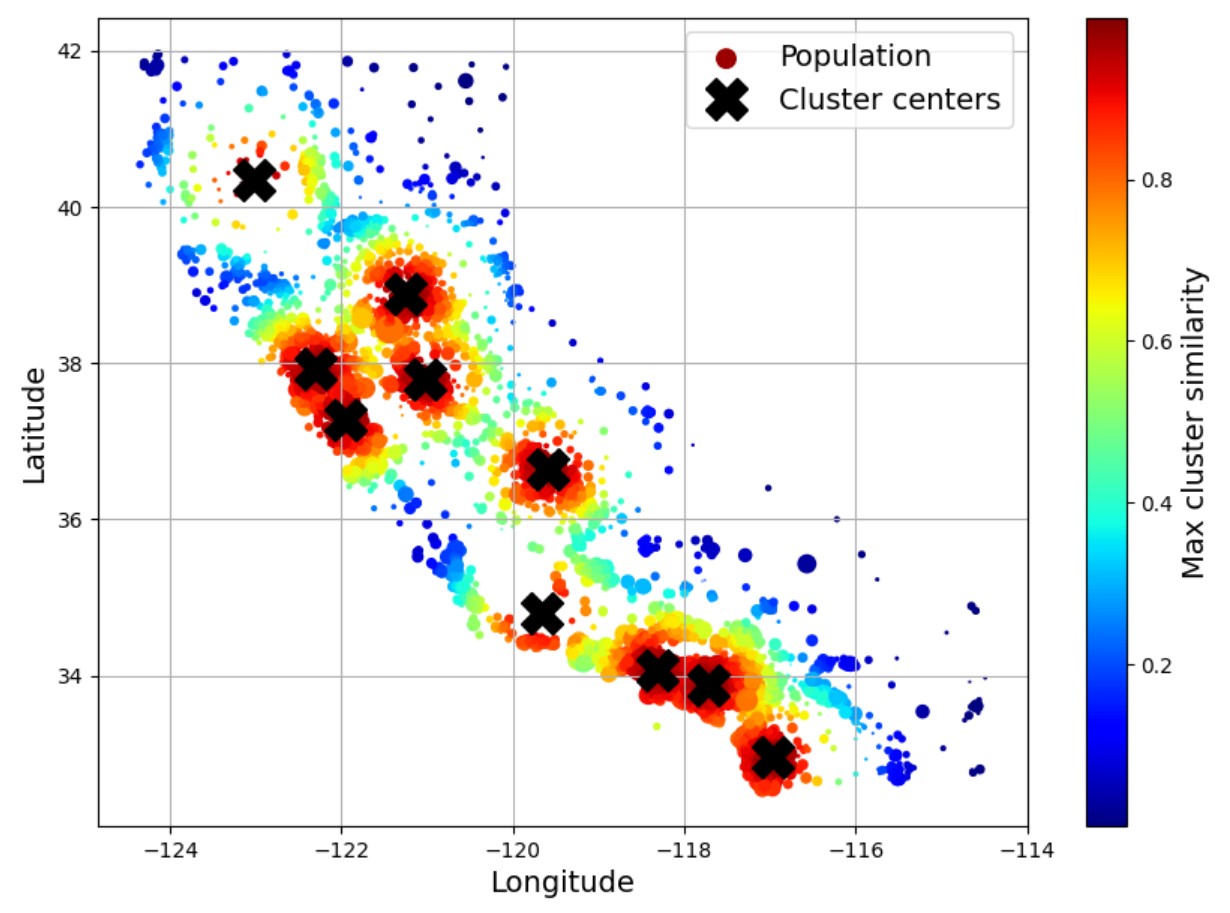
아래 그래프를 위 결과를 이용하여 그릴 수 있다.
🗙 표시는 각 군집의 센트로이드centroid, 즉 각 군집의 중심 구역을 표시한다.
색상은 센트로이드 구역과의 유사도를 가리킨다. 빨강색의 구역이 센트로이드 구역과의 유사도가 1에 가깝다.
2.6. 파이프라인#
모든 전처리 단계가 정확한 순서대로 진행되어야 한다.
이를 위해 사이킷런의 Pipeline 클래스를 이용하여 여러 변환기를 순서대로
실행하는 변환기 파이프라인을 생성해서 활용한다.
사이킷런에서 제공하는 파이프라인 관련 주요 API는 다음과 같다.
Pipeline클래스make_pipeline()함수ColumnTransformer클래스make_column_selector()함수make_column_transformer()함수
2.6.1. Pipeline 클래스#
예를 들어, 수치형 특성을 대상으로 결측치를 중위수로 채우는 정제와 표준화를 연속적으로 실행하는 파이프라인은 다음과 같이 정의한다.
num_pipeline = Pipeline([("impute", SimpleImputer(strategy="median")),
("standardize", StandardScaler())])
Pipeline 인스턴스를 생성할 때 추정기명과 추정기로 이루어진 쌍들의 리스트를
이용한다.
단, 마지막 추정기를 제외한 나머지 추정기는 모두
fit_transform() 메서드를 지원하는 변환기어야 한다.
파이프라인으로 정의된 추정기의 유형은 마지막 추정기의 유형과 동일하다.
따라서 num_pipeline 은 변환기다.
num_pipeline.fit() 를 호출하면 마지막 추정기 이전까지의 변환기에 대해서는
fit_transform() 메소드가 연속적으로 호출되고,
마지막 변환기의 fit() 메서드 최종 호출된다.
make_pipeline() 함수
파이프라인에 포함되는 변환기의 이름이 중요하지 않다면 make_pipeline() 함수를 이용하여
Pipeline 객체를 생성할 수 있다. 이름은 자동으로 지정된다.
위 파이프라인과 동일한 파이프라인 객체를 다음과 같이 생성할 수 있다.
from sklearn.pipeline import make_pipeline
num_pipeline = make_pipeline(SimpleImputer(strategy="median"),
StandardScaler())
2.6.2. ColumnTransformer 클래스#
ColumnTransformer 클래스는 특성별로
파이프라인 변환기를 지정하여 특성별 전처리를 실행할 수 있다.
예를 들어, 수치형 특성엔 num_pipeline 변환기를, 범주형 특성엔 OneHotEncoder 변환기를 적용하는
변환기를 다음과 같이 구현할 수 있다.
# 수치형 특성 리스트 지정
num_attribs = ["longitude", "latitude", "housing_median_age", "total_rooms",
"total_bedrooms", "population", "households", "median_income"]
# 범주형 특성 리스트 지정
cat_attribs = ["ocean_proximity"]
# 범주형 특성 변환 파이프라인
cat_pipeline = make_pipeline(
SimpleImputer(strategy="most_frequent"),
OneHotEncoder(handle_unknown="ignore"))
# 전체 특성 변환기
preprocessing = ColumnTransformer([
("num", num_pipeline, num_attribs),
("cat", cat_pipeline, cat_attribs)])
make_column_selector() 함수
파이프라인에 포함되는 각 변환기를 적용할 특성을 일일이 나열하는 일이 어려울 수 있다.
이때 지정된 자료형을 사용하는 특성들만을 선택해주는 make_column_selector() 함수를
유용하게 활용할 수 있다.
make_column_selector(dtype_include=np.number): 수치형 특성 모두 선택make_column_selector(dtype_include=object): 범주형 특성 모두 선택
따라서 위 preprocessing 변환기를 아래와 같이 정의할 수 있다.
preprocessing = ColumnTransformer([
("num", num_pipeline, make_column_selector(dtype_include=np.number)),
("cat", cat_pipeline, make_column_selector(dtype_include=object)
])
make_column_transformer() 함수
ColumnTransformer 인스턴스에 포함되는 파이프라인의 이름이 중요하지 않다면
make_column_transformer() 함수를 이용할 수 있다.
사용 방식은 make_pipeline() 함수와 유사하다.
예를 들어 앞서의 preprocessing 변환기를 아래와 같이 정의할 수 있다.
preprocessing = make_column_transformer(
(num_pipeline, make_column_selector(dtype_include=np.number)),
(cat_pipeline, make_column_selector(dtype_include=object)),
)
2.6.3. 캘리포니아 데이터셋 변환 파이프라인#
ColumnTransformer 클래스와 Pipeline 클래스를 이용하여
캘리포니아 주택가격 데이터의 입력 데이터셋을 한꺼번에 변환하는
변환기를 다음 네 개의 변환기를 이용하여 구현한다.
(1) 비율 변환기
가구당 방 수, 침실 비율, 가구당 평균 가구원수 등 비율을 사용하는 특성을 새로 추가할 때 사용되는 변환기를 다음과 같이 정의한다.
def column_ratio(X):
return X[:, [0]] / X[:, [1]] # 1번 특성에 대한 0번 특성의 비율율
def ratio_name(function_transformer, feature_names_in):
return ["ratio"] # 새로 생성되는 특성값들의 특성명
ratio_pipeline = make_pipeline(
SimpleImputer(strategy="median"),
FunctionTransformer(column_ratio, feature_names_out=ratio_name),
StandardScaler()
)
(2) 로그 변환기
데이터 분포가 두터운 꼬리를 갖는 특성을 대상으로 로그 함수를 적용하는 변환기를 지정한다.
로그 변환기를 지정할 때 사용되는 feature_names_out="one-to-one"는 로그 변환되어 생성되는
특성값들의 특성명을 이전 특성명과 동일하게 지정하라는 의미이다.
보다 자세한 의미는 실제로 활용될 때 한 번 더 설명한다.
log_pipeline = make_pipeline(
SimpleImputer(strategy="median"),
FunctionTransformer(np.log, feature_names_out="one-to-one"),
StandardScaler()
)
(3) 군집 변환기
구역의 위도와 경도를 이용하여 구역들의 군집 정보를 새로운 특성으로 추가하는 변환기를 지정한다.
주의사항: 이전과는 달리 군집 분류를 위해 경도, 위도 정보만 이용한다.
cluster_simil = ClusterSimilarity(n_clusters=10, gamma=1., random_state=42)
(4) 기본 변환기
특별한 변환이 필요 없는 경우에도 기본적으로 결측치 문제 해결과 스케일을 조정하는 변환기를 사용한다.
default_num_pipeline = make_pipeline(
SimpleImputer(strategy="median"),
StandardScaler()
)
종합
앞서 언급된 모든 변환기를 특성별로 적용하는 변환기를
ColumnTransformer 클래스를 이용하여 정의한다.
remainder=default_num_pipeline는
그때까지 언급되지 않은 나머지 특성들을 처리하는 변환기를
키워드 인자로 지정한다.
remainder 매개변수의 키워드 인자로 나머지 특성을 삭제하는 것을 지정하는
drop 이 기본값이며, 그 이외에 passthrough는 나머지 특성은
변환하지 않고 그대로 두어야 함을 의미한다.
아래 코드에서는 주택 중위연령을 가리키는 housing_median_age 특성에는
기본 변환기를 적용한다.
preprocessing = ColumnTransformer([
("bedrooms", ratio_pipeline, ["total_bedrooms", "total_rooms"]), # 침실 비율
("rooms_per_house", ratio_pipeline, ["total_rooms", "households"]), # 가구당 방 수
("people_per_house", ratio_pipeline, ["population", "households"]), # 가구당 평균 가구원수
("log", log_pipeline, ["total_bedrooms", "total_rooms", "population", # 로그 변환
"households", "median_income"]),
("geo", cluster_simil, ["latitude", "longitude"]), # 구역별 군집 정보
("cat", cat_pipeline, make_column_selector(dtype_include=object)), # 범주형 특성 전처리
],
remainder=default_num_pipeline) # 주택 중위연령(housing_median_age) 대상
아래 코드는 위 변환기를 이용하여 정제와 전처리를 입력 데이터셋의 모든 특성에 대해 특성별로 실행한다.
housing_prepared = preprocessing.fit_transform(housing)
변환된 데이터셋의 특성은 총 24개이며 다음과 같다.
비율 변환기 적용: 3개의 새로운 특성 생성.
위도와 경도: 10개의 특성으로 변환. 2개의 특성을 빼고 10개 특성 새로 추가.
해안근접도: 5개의 특성으로 변환. 1개의 특성을 빼고 10개 특성 추가.
나머지 특성은 새로운 특성을 추가로 생성하지는 않음.
preprocessing.get_feature_names_out()
array(['bedrooms__ratio', 'rooms_per_house__ratio',
'people_per_house__ratio', 'log__total_bedrooms',
'log__total_rooms', 'log__population', 'log__households',
'log__median_income', 'geo__Cluster 0 similarity',
'geo__Cluster 1 similarity', 'geo__Cluster 2 similarity',
'geo__Cluster 3 similarity', 'geo__Cluster 4 similarity',
'geo__Cluster 5 similarity', 'geo__Cluster 6 similarity',
'geo__Cluster 7 similarity', 'geo__Cluster 8 similarity',
'geo__Cluster 9 similarity', 'cat__ocean_proximity_<1H OCEAN',
'cat__ocean_proximity_INLAND', 'cat__ocean_proximity_ISLAND',
'cat__ocean_proximity_NEAR BAY', 'cat__ocean_proximity_NEAR OCEAN',
'remainder__housing_median_age'], dtype=object)
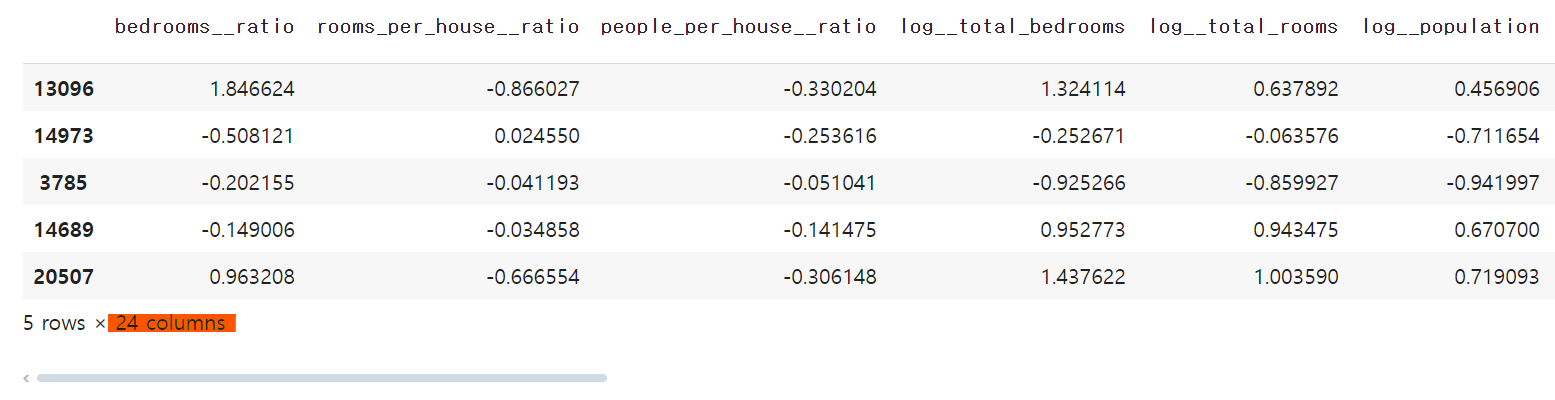
변환된 데이터셋을 데이터프레임으로 표현하면 다음과 같다. 특성이 24개로 너무 많아서 아래 그림에서는 6개의 특성만 보여준다.
housing_prepared_df = pd.DataFrame(housing_prepared,
columns=preprocessing.get_feature_names_out(),
index=housing.index)
housing_prepared_df.head()
2.7. 모델 선택과 훈련#
훈련셋 준비가 완료된 상황에서 모델을 선택하고 훈련시키는 일이 남아 있다.
사이킷런이 제공하는 예측기 모델을 사용하면 훈련은 기본적으로 간단하게 진행된다. 여기서는 사이킷런이 제공하는 세 종류의 회귀 모델의 사용법과 결과의 차이를 간단하게 살펴본다. 각 모델의 자세한 특징과 상세 설명은 이어지는 장에서 하나씩 다룬다.
주의사항: 여기서 소개되는 모든 예측기는 앞서 설명한 전처리 과정과 함께 하나의 파이프라인으로 묶여서 활용된다.
2.7.1. 모델 훈련과 평가#
사이킷런의 회귀 모델을 훈련시키고 모델의 훈련 결과를 평가하는 방식은 거의 동일하다. 여기서 언급하는 모델은 다음 세 종류이다.
회귀 모델을 사용하는 이유는 구역별 주택 중위가격인 연속형 값을 예측해야 하기 때문이다. 또한 회귀 모델의 성능 평가는 일반적으로 RMSE(root-mean-square error, 평균 제곱근 오차)로 계산된다. RMSE(평균 제곱근 오차)는 예측 오차의 제곱의 평균값에 루트를 쒸운 값이며, 0에 가까울 수록 모델의 예측 성능이 좋다.
선형 회귀 모델: 입력 데이터셋의 특성과 타깃 사이의 선형 관계를 훈련을 통해 학습한다.
모델 지정
from sklearn.linear_model import LinearRegression lin_reg = make_pipeline(preprocessing, LinearRegression())
모델 훈련
lin_reg.fit(housing, housing_labels)
모델 활용
lin_reg.predict(housing)
모델 성능 측정: RMSE(평균 제곱근 오차) 활용
from sklearn.metrics import mean_squared_error lin_rmse = mean_squared_error(housing_labels, housing_predictions, squared=False)
모델 훈련 평가
RMSE(
lin_rmse)가 68687.89 정도로 나쁨.훈련셋에 대한 성능이 낮아서 과소적합 현상이 발생했다고 말할 수 있음.
보다 좋은 특성을 찾거나 더 강력한 모델을 적용해야 함.
결정트리 회귀 모델: 결정트리 회귀 모델은 데이터에서 복잡한 비선형 관계를 훈련을 통해 학습한다.
모델 지정
from sklearn.tree import DecisionTreeRegressor tree_reg = make_pipeline(preprocessing, DecisionTreeRegressor(random_state=42))
모델 훈련
tree_reg.fit(housing, housing_labels)
모델 활용
housing_predictions = tree_reg.predict(housing)
모델 성능 측정: RMSE 활용
tree_rmse = mean_squared_error(housing_labels, housing_predictions,
squared=False)
모델 훈련 평가
RMSE(
tree_rmse)가 0으로 완벽해 보임.모델이 훈련셋에 심각하게 과대적합 되었음을 반영함.
실전 상황에서 RMSE가 0이 되는 것은 불가능함.
테스트셋에 대한 RMSE는 매우 높게 나옴.
랜덤 포레스트 회귀 모델: 랜덤 포레스트random forest 회귀 모델은 여러 개의 결정트리를 동시에 훈련시킨 후 각 모델의 예측값의 평균값 등을 이용하는 모델이다. 각 모델은 서로 다른 훈련셋을 이용하여 훈련한다.
모델 지정: 사이킷런의
RandomForestRegressor모델은 기본값으로 100개의 결정트리를 동시에 훈련시킨다.
from sklearn.ensemble import RandomForestRegressor
forest_reg = make_pipeline(preprocessing,
RandomForestRegressor(n_estimators=100, random_state=42))
모델 훈련
forest_reg.fit(housing, housing_labels)
모델 활용
housing_predictions = forest_reg.predict(housing)
모델 성능 측정: RMSE 활용
forest_rmse = mean_squared_error(housing_labels, housing_predictions,
squared=False)
모델 훈련 평가
RMSE(
tree_rmse)가 17474 정도로 선형회귀 모델 보다 헐씬 낮음.테스트셋에 대한 RMSE가 보다 높기는 함.
하지만 결정트리 모델 보다 과대적합 현상이 매우 적게 발생함.
2.7.2. 교차 검증#
교차 검증cross validation을 이용하여 모델의 성능을 보다 객관적으로 평가할 수 있다. 사이킷런에서 제공하는 k-겹 교차 검증 과정은 다음과 같다.
폴드 생성: 훈련셋을 폴드fold라 불리는 k-개의 부분 집합으로 무작위로 분할
모델 훈련: 총 k 번 훈련
매 훈련마나다 하나의 폴드를 선택하여 검증 데이터셋으로 지정
나머지 (k-1) 개의 폴드를 대상으로 훈련
매 훈련이 끝날 때마다 선택된 검증 데이터셋을 이용하여 모델 평가
매번 다른 폴드 활용
최종평가: k-번 훈련 평가 결과의 평균값 활용
아래 그림은 5-겹 교차 검증을 묘사한다.
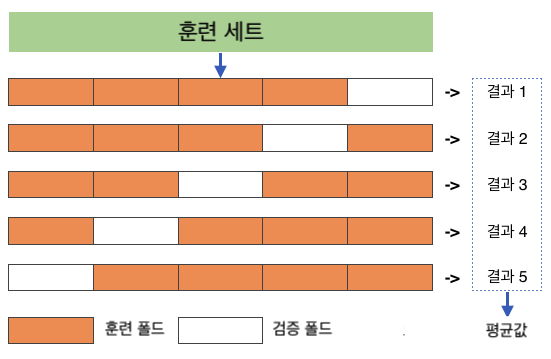
사이킷런의 cross_val_score() 함수
cross_val_score() 함수는 지정된 모델을 k-겹 교차 검증을 이용하여 평가한다.
훈련중인 모델의 성능을 측정한다.
아래 코드는 결정트리 모델에 대해 교차 검증을 실행하며, 사용된 키워드 인자는 다음과 같다.
scoring="neg_mean_squared_error"옵션훈련중인 모델의 성능을 측정하는 효용함수 지정
모델의 성능 측정값은 높을 수록 좋은 성능으로 평가되기에 회귀 모델의 경우 일반적으로 RMSE의 음숫값을 사용함.
cv=10: 10-겹 교차 검증 진행
from sklearn.model_selection import cross_val_score
tree_rmses = -cross_val_score(tree_reg, housing, housing_labels,
scoring="neg_root_mean_squared_error", cv=10)
cv=10 설정에 의해 10 개의 폴드를 사용하며 매번 RMSE를 측정한다.
pd.Series(tree_rmses).describe()
count 10.000000
mean 66868.027288
std 2060.966425
min 63649.536493
25% 65338.078316
50% 66801.953094
75% 68229.934454
max 70094.778246
dtype: float64
선형회귀 모델에 대한 교차 검증: 결정트리 모델의 교차 검증 보다 약간 나쁨.
lin_rmses = -cross_val_score(lin_reg, housing, housing_labels,
scoring="neg_root_mean_squared_error", cv=10)
pd.Series(lin_rmses).describe()
count 10.000000
mean 69858.018195
std 4182.205077
min 65397.780144
25% 68070.536263
50% 68619.737842
75% 69810.076342
max 80959.348171
dtype: float64
랜덤 포레스트 회귀 모델에 대한 교차 검증: 래덤 포레스트 모델에 대한 교차 검증을 적용하면 폴드 수에 비례하여 훈련 시간이 더 오래 걸리지만 성능은 훨씬 좋음.
forest_rmses = -cross_val_score(forest_reg, housing, housing_labels,
scoring="neg_root_mean_squared_error", cv=10)
pd.Series(forest_rmses).describe()
count 10.000000
mean 47019.561281
std 1033.957120
min 45458.112527
25% 46464.031184
50% 46967.596354
75% 47325.694987
max 49243.765795
dtype: float64
scoring 키워드 인자
교차 검증에서 모델의 성능 평가 기준을 지정하는 scoring 키워드 인자는
사용되는 모델의 종류에 따라 다양하게 지정할 수 있다.
현재 사용 가능한 평가 방식은
사이킷런의 Metrics and Scoring 문서에서
확인할 수 있다.
2.8. 모델 미세 조정#
지금까지 살펴 본 모델 중에서 랜덤 포레스트 회귀 모델의 성능이 가장 좋았다. 이렇게 가능성이 높은 모델을 찾은 다음엔 모델의 세부 설정(하이퍼파라미터)을 조정하거나 성능이 좋은 모델 여러 개를 이용하여 모델의 성능을 최대한 끌어올린다.
이런 방식으로 잘 훈련된 모델의 성능을 좀 더 끌어 올리는 방법을 모델 미세 조정fine tuning이라 한다. 모델 미세 조정은 보통 다음 세 가지 방식을 많이 사용한다.
그리드 탐색
랜덤 탐색
앙상블 학습
하이퍼파라미터 vs. 파라미터
사이킷런 클래스의 하이퍼파라미터hyperparameter는
해당 클래스의 객체를 생성할 때 생성자 메서드의 인자로 사용되는 값들을 가리킨다.
반면에 파라미터parameter는
fit() 메서드가 데이터셋으로부터 추출한 정보에 해당하는 값을 가리킨다.
추정기, 변환기, 예측기는 각각의 역할에 맞는 파라미터를 계산한다.
사이킷런의 모든 클래스는 적절한 하이퍼파라미터로 초기화되어 있으며 데이터 변환과 값 예측에 필요한 모든 파라미터를 효율적으로 관리한다.
2.8.1. 그리드 탐색#
지정된 하이퍼파라미터의 모든 조합에 대해 교차 검증을 진행하여 최적의 모델을 생성하는 하이퍼파라미터 조합을 찾는 기법이다.
GridSearchCV 클래스
아래 코드는 랜덤 포레스트 모델을 대상으로 그리드 탐색을 실행하며 총 (3x3 + 2x3 = 15) 가지의 모델의 성능을 확인한다.
(군집수 3 가지) * (최대특성수 3 가지) + (군집수 2 가지) * (최대특성수 3 가지)
또한 3-겹 교차 검증(cv=3)을 진행하기에 모델 훈련을 총 45(=15x3)번 진행한다.
from sklearn.model_selection import GridSearchCV
full_pipeline = Pipeline([
("preprocessing", preprocessing),
("random_forest", RandomForestRegressor(random_state=42)),
])
# 3*3 + 2*3 조합 확인
param_grid = [
{'preprocessing__geo__n_clusters': [5, 8, 10],
'random_forest__max_features': [4, 6, 8]},
{'preprocessing__geo__n_clusters': [10, 15],
'random_forest__max_features': [6, 8, 10]},
]
# 3-겹 교차 검증 활용 훈련
grid_search = GridSearchCV(full_pipeline, param_grid, cv=3,
scoring='neg_root_mean_squared_error')
grid_search.fit(housing, housing_labels)
best_params_ 속성
그리드 탐색을 통해 찾아낸 최적의 하이퍼파라미터 조합은 다음과 같다.
grid_search.best_params_
{'preprocessing__geo__n_clusters': 15, 'random_forest__max_features': 6}
best_estimator_ 속성
그리드 탐색을 통해 찾아낸 최적의 모델은 best_estimator_ 속성에 저장된다.
grid_search.best_estimator_
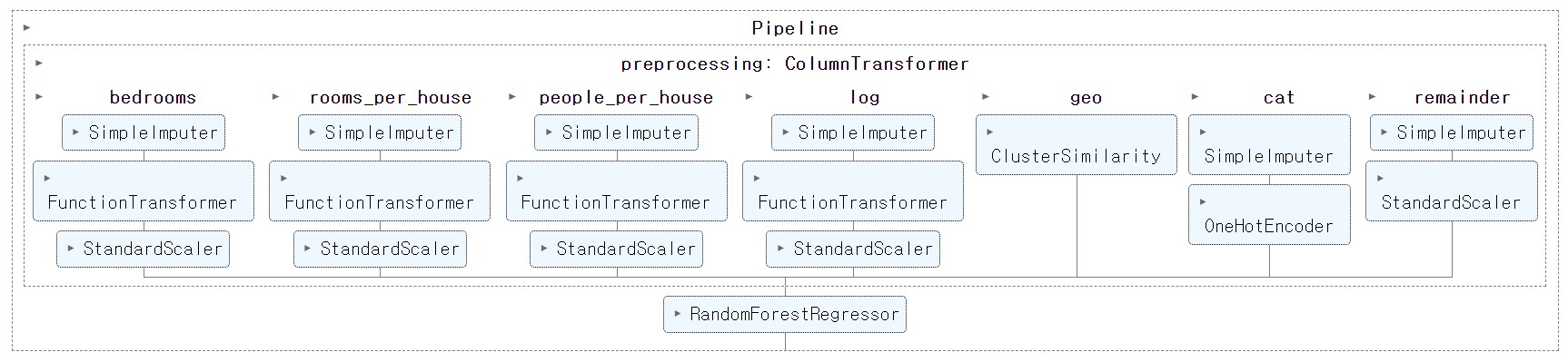
최고 성능의 랜덤 포레스트 회귀 모델에 대한 교차 검증의 RMSE는 44042 정도로
이전보다 좀 더 좋아졌다.
해당 값은 grid_search.cv_results_ 속성에서 확인할 수 있다.
2.8.2. 랜덤 탐색#
그리드 탐색은 적은 수의 하이퍼파라미터 조합을 실험해볼 때만 유용하다. 반면에 하이퍼파라미터의 탐색 공간이 크면 랜덤 탐색이 보다 효율적으로 최적의 하이퍼파라미터 조합을 찾아낸다.
RandomizedSearchCV 클래스
아래 코드는 다음 두 하이퍼파라미터를 대상으로
10번(n_iter=10) 무작위 선택을 지정된 범위 내에서 진행한다.
preprocessing__geo__n_clustersrandom_forest__max_features
또한 3-겹 교차 검증(cv=3)을 진행하기에 모델 훈련을 총 30(=10x30)번 진행한다.
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint
# 하이퍼파라미터 탐색 공간 지정
param_distribs = {'preprocessing__geo__n_clusters': randint(low=3, high=50),
'random_forest__max_features': randint(low=2, high=20)}
# 10개의 하이퍼파라미터 무작위 선택, 3-겹 교차 검증 활용
rnd_search = RandomizedSearchCV(
full_pipeline, param_distributions=param_distribs, n_iter=10, cv=3,
scoring='neg_root_mean_squared_error', random_state=42)
rnd_search.fit(housing, housing_labels)
랜덤 탐색을 통해 찾아낸 최적의 모델과 최적의 하이퍼파라미터 조합 확인방법은 그리드 탐색의 경우와 동일하다.
군집수: 45개
최대 특성수: 9개
rnd_search.best_params_
{'preprocessing__geo__n_clusters': 45, 'random_forest__max_features': 9}
최고 성능의 랜덤 포레스트 회귀 모델에 대한 교차 검증의 RMSE는 41995 정도로
그리드 탐색에서 찾은 모델보다 좀 더 좋아졌다.
해당 값은 rnd_search.cv_results_ 속성에서 확인할 수 있다.
무작위 선택 확률분포 함수 활용
랜덤 탐색을 하려면 특정 옵션 변수갈들을 무작위로 선택해주는 확률분포 함수를 지정해야 한다.
이전 코드의 랜덤 탐색에서는 이산 균등 분포를 사용하는 randint() 함수를 이용하였다.
'preprocessing__geo__n_clusters': randint(low=3, high=50)
'random_forest__max_features': randint(low=2, high=20)
scipy는 이외에 다른 종류의 확률 분포 함수를 지원한다.
예를 들어, 지정된 구간에서의 부동소수점을 선택해야 한다면
연속 균등 분포 함수인 scipy.stats.uniform(a, b)를 이용할 수 있다.
기타 모델 미세 조정 도구
다양한 방식의 모델 미세 조정에 대한 보다 자세한 정보는 Best Tools for Model Tuning and Hyperparameter Optimization을 참고할 수 있다.
2.8.3. 앙상블 학습#
결정 트리 모델 하나보다 랜덤 포레스트처럼 여러 모델로 이루어진 모델이 보다 좋은 성능을 낼 수 있다. 또한 최고 성능을 보이는 여러 개의 모델을 조합하면 보다 좋은 성능을 얻을 수 있다. 이렇게 성능이 좋은 여러 개의 모델을 함께 학습하여 예측값을 지정하는 방식인 앙상블 학습에 대해 6장에서 자세히 다룬다.
2.8.4. 최적 모델 활용#
모델 미세 조정을 통해 구한 최적의 모델을 분석해서 훈련에 사용된 데이터셋에 대한 중요한 통찰을 얻을 수 있다. 예를 들어, 최적의 랜덤 포레스트 모델로부터 모델의 예측값에 영향을 주는 특성들의 상대적 중요도를 확인할 수 있다.
캘리포니아 주택 가격 예측 모델의 경우 랜덤 탐색을 통해 찾아낸 최적의 모델에서
feature_importances_를 확인하면 다음 정보를 얻는다.
log__median_income특성이 해당 구역의 집값 예측이 가장 중요함.해안 근접도 특성 중에서 특히
INLAND특성이 집값 예측에 나름 중요한 역할을 수행함.
# 최적 모델
final_model = rnd_search.best_estimator_
# 특성별 상대적 중요도
feature_importances = final_model["random_forest"].feature_importances_
# 중요도 내림차순 정렬
sorted(zip(feature_importances,
final_model["preprocessing"].get_feature_names_out()),
reverse=True)
[(0.18694559869103852, 'log__median_income'),
(0.0748194905715524, 'cat__ocean_proximity_INLAND'),
(0.06926417748515576, 'bedrooms_ratio__bedrooms_ratio'),
(0.05446998753775219, 'rooms_per_house__rooms_per_house'),
(0.05262301809680712, 'people_per_house__people_per_house'),
(0.03819415873915732, 'geo__Cluster 0 similarity'),
[...]
(0.00015061247730531558, 'cat__ocean_proximity_NEAR BAY'),
(7.301686597099842e-05, 'cat__ocean_proximity_ISLAND')]
주의사항: 모델이 전처리와 함게 하나의 파이프라인으로 묶여 있음에 주의한다.
따라서 위 코드에서 사용된 final_model["random_forest"]가 예측기를 가리킨다.
full_pipeline = Pipeline([
("preprocessing", preprocessing),
("random_forest", RandomForestRegressor(random_state=42)),
])
테스트셋 활용 최종 평가
최고 성능 모델을 테스트셋에 적용하여 훈련된 모델의 성능을 최종 평가한다. 지금까지 확인한 모델 중에서 가장 좋은 성능을 보인다.
X_test = strat_test_set.drop("median_house_value", axis=1)
y_test = strat_test_set["median_house_value"].copy()
final_predictions = final_model.predict(X_test)
final_rmse = mean_squared_error(y_test, final_predictions, squared=False)
print(final_rmse)
41424.40026462184
테스트셋에 적용된 변환기
위 코드에서 final_model.predict(X_test)를 실행하면 먼저
모델에 포함된 전처리 과정이 테스트셋에 대해 먼저 진행된다.
그런데 훈련셋에 대해서와는 달리 전처리를 처리하는 변환기의 fit_transform() 메서드가 아닌
transform() 메서드가 사용된다.
이유는 변환기가 데이터 변환을 위해 필요한 정보를 훈련셋에 대해 fit() 메서드를 먼저 적용하여
알아내는 데 이 정보를 그대로 테스트셋에 대해 활용하기 때문이다.
사이킷런의 변환기와 예측기는 모두 fit() 메소드에 의해 추출된 정보를 자체 객체에 속성으로 저장하며
필요에 따라 재활용한다.
예제를 이용한 보다 자세한 설명은 아래 링크를 참조한다.
2.9. 최적 모델 저장과 활용#
최적의 모델을 훈련시키는 과정이 매우 길 수 있다. 따라서 한 번 훈련된 좋은 모델은 저장해 놓고 필요할 때 불러와서 바로 사용할 수 있도록 해둔다. 이 뿐만 아니라 업데이트된 모델이 적절하지 않은 경우 이전 모델로 되돌려야 하는 상황이 발생할 수도 있다.
모델의 저장과 불러오기는 joblib 모듈을 활용한다.
저장하기
import joblib joblib.dump(final_model, "my_california_housing_model.pkl")
불러오기와 활용
final_model_reloaded = joblib.load("my_california_housing_model.pkl") final_model_reloaded.predict(X_test)
