결정트리

6. 결정트리#

감사의 글

자료를 공개한 저자 오렐리앙 제롱과 강의자료를 지원한 한빛아카데미에게 진심어린 감사를 전합니다.

소스코드

본문 내용의 일부를 파이썬으로 구현한 내용은 (구글코랩) 결정트리에서 확인할 수 있다.

주요 내용

결정트리 훈련과 활용
CART 알고리즘
지니 불순도 vs. 엔트로피
결정트리 규제
회귀 결정트리
결정트리 단점

슬라이드

본문 내용을 요약한 슬라이드를 다운로드할 수 있다.

6.1. 결정트리 훈련과 활용#

6.1.1. 결정트리 훈련#

아래 코드는 붓꽃 데이터셋을 대상으로 사이킷런의 DecisionTreeClassifier 모델을 훈련시킨다. 특성은 꽃잎의 길이와 너비만을 사용하여 세 개의 품종으로 분류하는 다중 클래스 모델을 훈련시킨다. max_depth는 결정트리의 최대 깊이를 지정하는 하이퍼파라미터며, 여기서는 2로 지정한다. 기본값은 None이며, 이는 최대 깊이를 제한하지 않음을 의미한다.

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier

iris = load_iris(as_frame=True)
X_iris = iris.data[["petal length (cm)", "petal width (cm)"]].values
y_iris = iris.target

tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf.fit(X_iris, y_iris)

결정트리 모델과 데이터 전처리

결정트리 모델을 훈련시키기 위해 입력 데이터셋의 전처리는 일반적으로 필요 없다.

6.1.2. 결정트리 시각화#

사이킷런의 export_graphviz() 함수를 이용하여 학습된 결정트리를 그래프로 시각화한다. 또한 pdf, png 등 많은 종류의 파일로 변환이 가능하다.

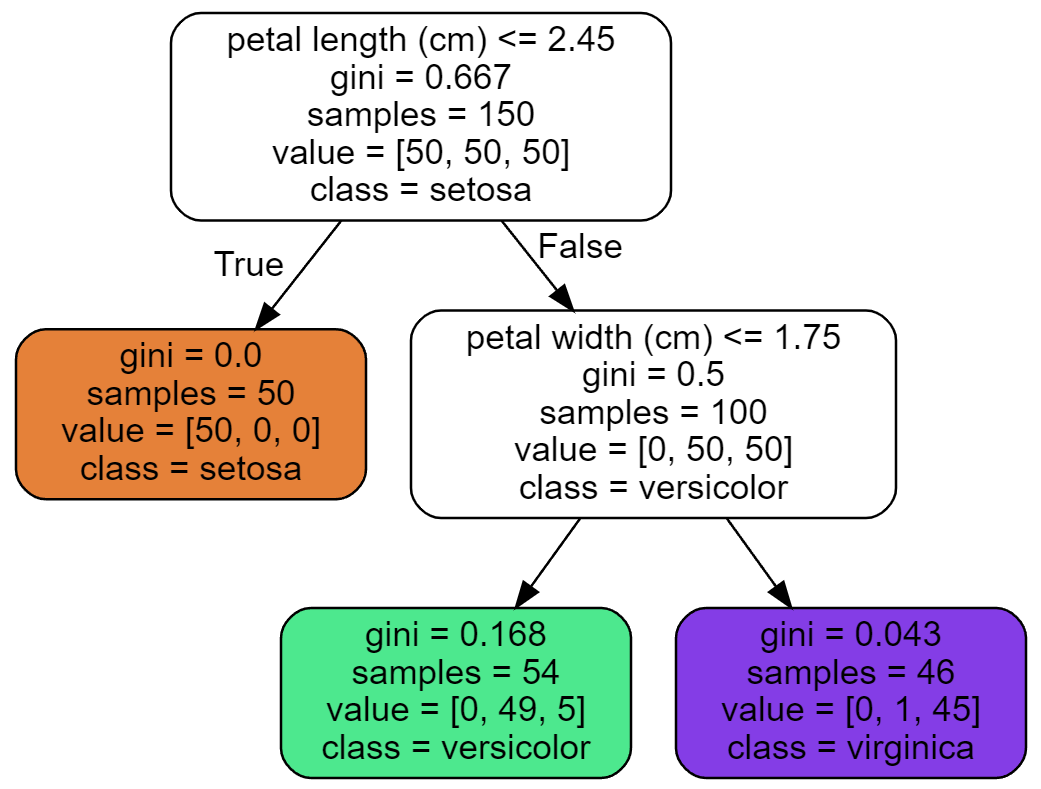
결정트리의 각 노드에 포함된 속성은 다음과 같다.

gini: 노드의 지니 불순도
samples: 노드에 속하는 샘플수
value: 각각의 범주(클래스)에 속하면서 노드에 포함된 샘플 수. 타깃 정보 활용.
class: 가장 높은 비율을 차지하는 범주. 비율이 동일한 경우 낮은 인덱스의 범주 선택.

트리와 노드

트리rooted tree는 아래 성질을 만족하는 노드node와 이음선edge들로 이루진다.

루트로 사용되는 하나의 노드가 있다.
루트를 제외한 모든 노드는 부모 노드로부터 오는 진입 이음선으로 연결된다.
루트로부터 임의의 노트로 연결되는 경로가 유일하게 존재한다.

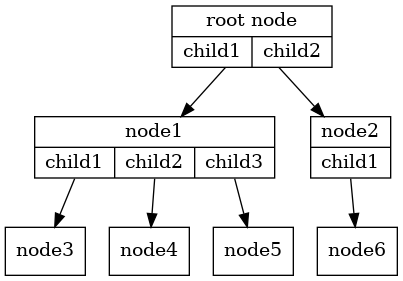
트리의 노드는 가지 분할이 시작되는 지점이며 부모 노드와 자식 노드를 가질 수 있다.

루트root 노드: 맨 상단에 위치한 노드. 부모 노드를 갖지 않음.
잎leaf 노드: 더 이상의 가지분할이 발생하지 않는 노드. 자식 노드를 갖지 않음.

노드의 인덱스

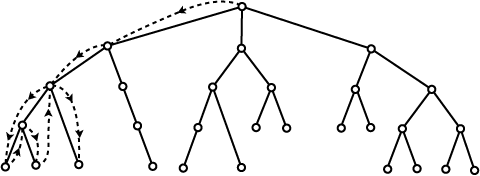
노드의 인덱스는 깊이 우선 탐색depth-first-search(DFS) 방식으로 이루어진다. 즉, 루트 노드를 0으로 시작해서 아래 그림에서처럼 가능한한 계속해서 왼쪽 자식부터 인덱스를 지정한다.

루트 노드에서 시작해서 갈 수 있는 한 가장 왼쪽 자식 노드로 탐색 진행
잎 노드에 다달한 경우 탐색 대상이 될 수 있는 자식 노드를 갖는 가장 가까운 조상 노드로 이동해서 깊이 우선 탐색 진행. 단, 한 번 탐색한 자식 노드는 무시.

지니 불순도

각 노드의 지니 불순도는 노드에 포함된 샘플들이 여러 범주에 퍼져있는 정도를 계산한다. 노드의 모든 샘플이 하나의 범주에 속하면 지니 불순도는 0, 골고루 퍼져

다음처럼 계산된다. 아래 수식에서 \(G_i\) 는 \(i\)-번 인덱스 노드의 지니 불순도를 가리킨다.

\[G_i = 1 - \sum_{k=0}^{K-1} (p_{i,k})^2\]

\(p_{i,k}\): \(i\) 번째 노드에 있는 훈련 샘플 중 범주 \(k\)에 속한 샘플의 비율
\(K\): 범주(클래스)의 개수

예를 들어, 깊이 2의 왼편 노드 \(G_3\)의 지니 불순도는 0.168로 계산된다.

\[G_3 = 1 - (0/54)^2 - (49/54)^2 - (5/54)^2 = 0.168\]

반면에 깊이 1의 왼편 노드 \(G_1\)에는 세토사 품종 55개만 포함되어 있어서 지니 불순도가 0이다.

\[G_1 = 1 - (55/55)^2 - (0/55)^2 - (0/55)^2 = 0\]

6.1.3. 범주 예측#

예를 들어 꽃잎 길이와 너비가 각각 5cm, 1.5cm 인 샘플의 범주는 아래 과정을 거처 주어진 데이터가 속한 잎 노드의 속성을 확인하여 예측한다.

루트에서 시작한다.
분할 1단계: 꽃잎 길이가 2.45cm 보다 크기에 오른편 자식 노드로 이동한다.
분할 2단계: 꽃잎 너비가 1.75cm 이하이기에 왼편 자식 노드로 이동한다. 해당 노드가 잎 노드이고 버시컬러의 비율이 가장 높기에 버시컬러 품종으로 예측한다.

이처럼 결정트리 모델은 예측값의 계산과정을 명확하게 추적할 수 있다. 이런 의미에서 결정트리 모델은 화이트박스whitebox 모델이다. 반면에 머신러닝, 딥러닝의 대부분의 모델은 예측값의 생성과정을 추적하기 어려운 블랙박스blackbox 모델이다.

결정경계

max_depth=3으로 지정해서 모델을 다시 학습시키자.

tree_clf_deeper = DecisionTreeClassifier(max_depth=3, random_state=42)
tree_clf_deeper.fit(X_iris, y_iris)

graphviz를 이용하여 훈련된 결정트리 모델을 시각화하면 다음과 같다.

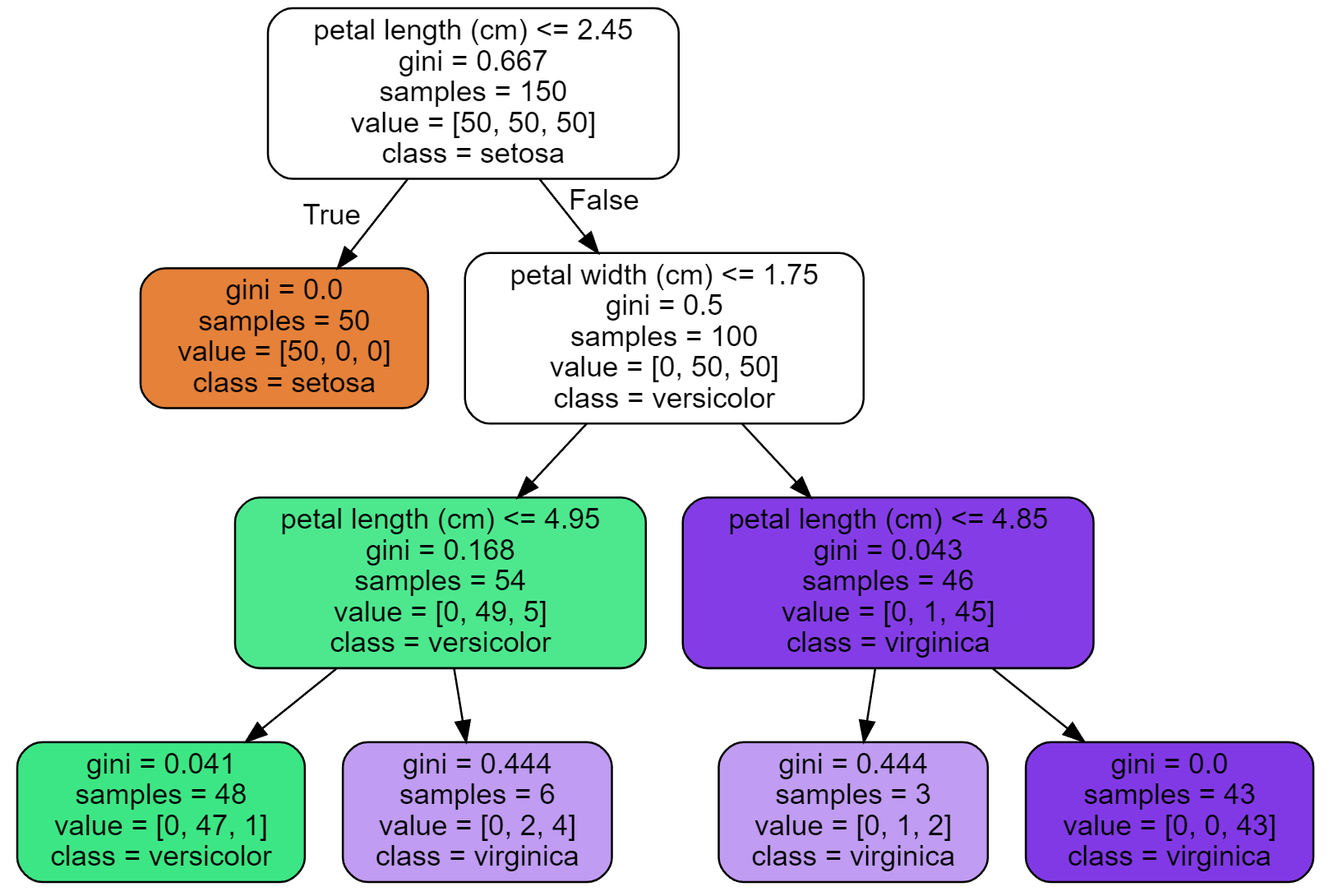
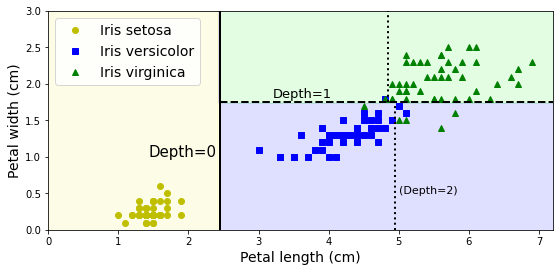
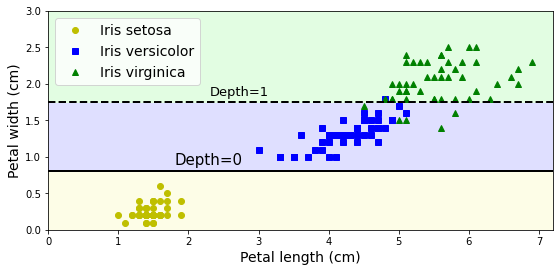
max_depth=3으로 지정해서 학습된 결정트리의 결정경계를 그래프로 그리면 다음과 같다.

1차 분할 기준: 꽃잎 길이 2.45cm. 트리 깊이 0에서 진행됨.
2차 분할 기준: 꽃잎 너비 1.75cm. 트리 깊이 1에서 진행됨.
3차 분할 기준: 꽃잎 길이 4.95cm. 트리 깊이 2에서 진행됨.
4차 분할 기준: 꽃잎 길이 4.85cm. 트리 깊이 2에서 진행됨.

분할에 사용된 값은 다음과 같이 확인한다.

tree_.threshold: 훈련된 결정트리 모델에 저장된 분할 임계점 정보.
0, 2, 3, 6: 분할이 발생한 노드들의 인덱스

th0, th1, th2a, th2b = tree_clf_deeper.tree_.threshold[[0, 2, 3, 6]]

6.1.4. 범주에 속할 확률#

주어진 샘플이 지정된 범주에 속할 확률은 다음과 같이 계산된다.

먼저, 해당 샘플이 포함되는 잎 노드를 확인한다.
해당 잎 노드에서 계산된 범주별 비율을 해당 범주에 속할 확률로 사용한다.

예를 들어, max_depth=2로 훈련된 tree_clf 모델은 꽃잎 길이와 너비가 각각 5cm, 1.5cm인 붓꽃을 깊이 2의 왼편 잎 노드인 \(G_3\)에 포함시킨다. 그리고 \(G_3\) 노드에 포함된 샘플들의 범주별 비율은 다음과 같다.

\[(0/54, 49/54, 5/54) = (0, 0.907, 0.093) \qquad\qquad (\text{세토사}, \text{버시컬러}, \text{버지니카})\]

버시컬러에 속할 확률이 90.7%로 가장 높기 때문에 해당 샘플은 버시컬러로 예측된다.

predict_proba() 메서드 vs. predict() 메서드

사이킷런의 결정트리 모델은 predict_proba() 메서드가 지정된 샘플의 범주별 추정 확률을 계산한다.

>>> tree_clf.predict_proba([[5, 1.5]]).round(3)
array([[0.   , 0.907, 0.093]])

반면에 predict() 메서드는 품종 범주를 예측하며, 가장 높은 추정 확률을 갖는 품종으로 지정한다.

>>> tree_clf.predict([[5, 1.5]]).round(3)
array([1])

반면에 max_depth=3으로 훈련된 tree_clf_deeper은 버지니카로 예측한다.

>>> tree_clf_deeper.predict_proba([[5, 1.5]]).round(3)
array([[0.   , 0.333, 0.667]])

>>> tree_clf_deeper.predict([[5, 1.5]]).round(3)
array([2])

6.2. CART 알고리즘#

CARTClassification and Regression Tree 분류 알고리즘

각 노드에서 아래 비용함수를 최소화 하는 특성 \(k\)와 해당 특성의 임곗값 \(t_k\)를 결정해서 분할하는 과정을 반복한다.

\(m\), \(m_\text{left}\), \(m_\text{right}\): 각각 부모와 왼쪽, 오른쪽 자식 노드에 속한 샘플 개수
\(G_\text{left}\), \(G_\text{right}\): 각각 왼쪽, 오른쪽 자식 노드의 지니 불순도

\[ J(k, t_k) = \frac{m_\text{left}}{m}\, G_\text{left} + \frac{m_\text{right}}{m}\, G_\text{right} \]

특성 \(k\)는 지정된 횟수 만큼 무작위로 선택되지만 선택된 특성의 임곗값 \(t_k\)는 모든 가능성, 즉 모든 훈련 샘플의 특성값을 대상으로 한다.

즉, 지니 불순도가 낮은 두 개의 부분집합으로 분할되도록 학습된다. 분할은 max_depth 등 규제에 의해 조절되거나 더 이상 불순도를 줄이는 분할이 불가능할 때까지 진행된다.

탐욕 알고리즘

\(J(k, t_k)\)를 가장 작게 하는 \(k\)와 \(t_k\)를 찾는 알고리즘은 탐욕 알고리즘이다. 이유는 대상으로 삼은 노드를 기준으로 지니 불순도가 가장 낮은, 즉 가장 순수한 두 개의 부분집합으로 분할하지만 이후의 분할에 대해서는 생각하지 않기 때문이다. 하지만 탐욕적 기법은 일반적으로 적절한 성능의 해를 찾아준다.

6.2.1. CART 알고리즘의 시간복잡도#

최적의 결정트리를 찾는 문제는 \(O(\exp(m))\) 복잡도를 갖는 동시에 NP-완전NP-complete이다. 따라서 매우 작은 훈련 세트에 대해서도 제대로 적용하기 어렵다.

하지만 탐욕 기법을 사용하는 CART 알고리즘의 시간 복잡도는 다음과 같다. \(n, m\)은 각각 특성수와 샘플수를 나타낸다.

각 노드에서 분류하는 데 걸리는 시간: \(O(n\cdot m\cdot \log_2(m))\)
결정트리를 완성하는 데 걸리는 시간: \(O(n\cdot m^2\cdot \log_2(m))\)

참고로 \(m\cdot \log_2(m)\) 은 정렬 후에 각 특성값을 임곗값으로 확인하는 데에 걸리는 시간과 연관된다.

반면에 학습된 결정트리가 예측에 필요한 시간은 \(O(\log_2 m)\)으로 매우 빠르다. 이유는 결정트리 모델은 균형 이진탐색트리balanced binary search tree에 가깝고 따라서 가장 깊은 경로가 \(\log_2(m)\) 정도이기 때문이다. 실제로 각 노드에서 하나의 특성만 분류기준으로 사용되기에 특성 수와 무관하게 이진트리의 경로를 추적할 수 있다.

6.2.2. 지니 불순도 vs. 엔트로피#

DecisionTreeClassifier의 criterion 하이퍼파라미터의 값을 'entropy' 로 지정하면 지니 불순도 대신에 샘플들의 무질서 정도를 측정하는 엔트로피entropy가 노드를 분할하는 기준으로 사용된다.

\(i\)-번 인덱스 노드의 엔트로피 \(H_i\) 는 다음과 같이 계산된다.

\[\begin{split}H_i = -\sum_{\substack{k=1\\p_{i,k}\neq 0}}^{K} p_{i,k} \log_2(p_{i,k})\end{split}\]

지니 불순도를 사용할 때와 비교해서 큰 차이가 나지는 않는다. 만약 차이가 난다면 엔트로피 방식이 결정 트리를 보다 좌우 균형이 잡히도록 자식 노드로 분할한다. 하지만 기본적으로 별 차이가 없고 지니 불순도 방식이 보다 빠르게 훈련되기에 기본값으로 지정되었다.

엔트로피 방식이 보다 균형 잡힌 이진탐색트리를 만드는 이유

특정 \(k\) 에 대해 \(p_{i,k}\) 가 \(0\) 에 매우 가까우면 \(-\log(p_{i,k})\) 가 매우 커진다. 이는 엔트로피 증가로 이어지기 때문에 결국 비용함수 \(J(k, t_k)\) 가 증가한다. 따라서 \(p_{i, k}\) 가 매우 작게되는 경우는 피하도록 학습하게 되고 결국 보다 균형 잡힌 두 개의 부분집합으로 분할하는 방향으로 유도된다.

6.2.3. 규제 하이퍼파라미터#

비파라미터 모델 vs. 파라미터 모델

결정트리 모델은 데이터에 대한 어떤 가정도 하지 않는다. 예를 들어, 노드를 분할할 때 어떤 제한도 가해지지 않으며, 따라서 학습되어야 하는 파라미터의 개수를 미리 알 수 없다. 이유는 노드를 분할 할 때마다 새로운 파라미터가 학습되기 때문이다. 이런 모델을 비파라미터 모델nonparametric model이라 부른다. 비파라미터 모델의 자유도는 제한되지 않기에 과대적합될 가능성이 높다.

반면에 선형 모델 등 지금까지 살펴 본 모든 모델은 학습되는 모델에 필요한 파라미터 수가 훈련 시작 전에 규정되며, 이런 이유로 과대적합 가능성이 상대적으로 작아진다. 이런 모델을 파라미터 모델parametric model이라 한다.

사이킷런 DecisionTreeClassifier 규제 하이퍼파라미터

앞서 살펴 본 max_depth 이외에 다양한 하이퍼파라미터를 이용해 모델의 과대적합 위험도를 줄이는 규제로 사용한다. 가장 많이 사용되는 규제는 다음과 같다. min_ 을 접두사로 갖는 하이퍼파라미터는 노드가 만족시켜야 하는 특성의 최소값을, max_ 를 접두사로 갖는 하이퍼파라미터는 노드가 만족시켜야 하는 특성의 허용된 최대값을 지정한다. 따라서 min_으로 시작하는 하이퍼파라미터는 값을 키우면 규제가 강해지고, max_로 시작하는 파라미터는 값을 줄여야 규제가 강해진다.

하이퍼파라미터	기능
`max_depth`	결정트리의 높이 제한
`min_samples_split`	노드 분할해 필요한 최소 샘플 개수
`min_samples_leaf`	잎 노드에 포함된 최소 샘플 개수
`max_leaf_nodes`	잎 노드 최대 개수
`max_features`	분할에 사용되는 특성 개수

규젝 적용 모델

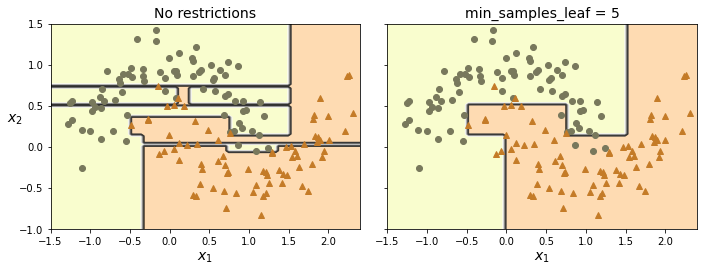
아래 코드는 min_samples_leaf=5 규제를 사용하는 모델(아래 그림 오른쪽)과 어느 규제도 사용하지 않은 모델(아래 그림 왼쪽)의 차이를 보여준다. 사용되는 훈련세트는 초승달 데이터셋이다.

왼쪽 결정트리: 과대적합 발생
오른쪽 결정트리: min_samples_leaf=5 규제 사용. 즉, 리프에 최소 5개 이상의 샘플이 포함되어야 함. 결과적으로 일반화 성능이 보다 좋은 결정트리가 생성됨.

from sklearn.datasets import make_moons

X_moons, y_moons = make_moons(n_samples=150, noise=0.2, random_state=42)

tree_clf1 = DecisionTreeClassifier(random_state=42)
tree_clf2 = DecisionTreeClassifier(min_samples_leaf=5, random_state=42)
tree_clf1.fit(X_moons, y_moons)
tree_clf2.fit(X_moons, y_moons)

6.3. 회귀 결정트리#

결정트리를 회귀 용도로 사용할 수 있다. 대표적으로 사이킷런의 DecisionTreeRegressor 클래스가 예측기 모델 학습에 사용된다.

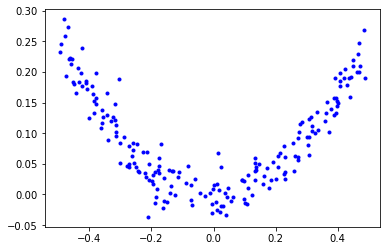
예를 들어, 잡음이 포함된 2차 함수 형태의 데이터셋을 이용하여 결정트리 회귀 모델을 훈련시켜 보자.

회귀 결정트리 훈련

아래 코드는 DecisionTreeRegressor 회귀 모델을 훈련시킨다. max_depth의 의미는 DecisionTreeClassifier의 경우와 동일하다.

tree_reg = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg.fit(X_quad, y_quad)

훈련된 결정트리는 다음과 같다.

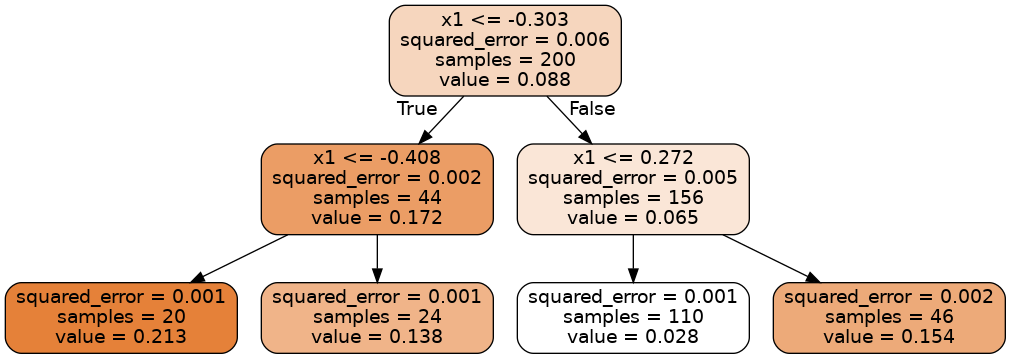
결정트리의 각 노드에 포함된 속성은 다음과 같다.

samples: 해당 노드에 속하는 훈련 샘플 수
value: 해당 노드에 속하는 훈련 샘플의 평균 타깃값
squared_error: 해당 노드에 속하는 훈련 샘플의 평균제곱오차(MSE)

회귀 결정트리 예측

x1=0.2 인 경우의 예측값은 아래 과정을 거처 주어진 데이터가 속한 잎 노드의 속성을 확인하여 예측한다.

루트에서 시작한다.
분할 1단계: -0.303 보다 크기에 오른쪽 자식 노드로 이동한다.
분할 2단계: 0.272 보다 작기에 왼쪽 자식 노드로 이동한다. 해당 노드가 잎 노드이고 value=0.028 이기에 0.028을 예측값으로 지정한다.

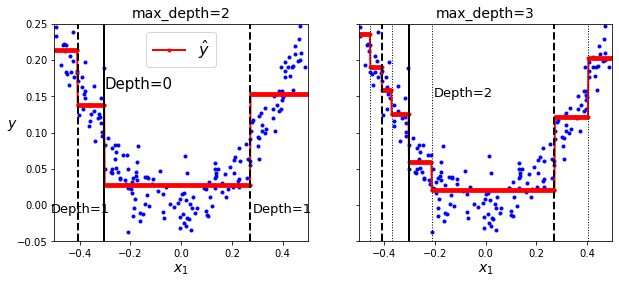
아래 왼쪽 그래프는 max_depth=2로, 오른쪽 그래프는 max_depth=3로 지정해서 훈련된 회귀 결정트리 예측 함수의 그래프이다.

검정 실선(Depth=0): 1차 분할 기준
검정 파선(Depth=1): 2차 분할 기준
(오른쪽 그래프) 검정 점선(Depth=2): 3차 분할 기준

회귀용 CART 알고리즘의 비용함수

분류의 경우처럼 탐욕적으로 아래 비용함수를 최소화 하는 특성 \(k\)와 해당 특성의 임곗값 \(t_k\)를 결정해서 분할하는 과정을 반복한다.

\(\text{MSE}_\text{node}\): 해당 노드의 평균제곱오차(MSE).
\(m_\text{node}\): 해당 노드에 속하는 샘플 수
\(y^{(i)}\): 샘플 \(i\)에 대한 실제 타깃값

\[\begin{split} \begin{align*} J(k, t_k) &= \frac{m_\text{left}}{m}\, \text{MSE}_\text{left} + \frac{m_\text{right}}{m}\, \text{MSE}_\text{right} \\[2ex] \text{MSE}_\text{node} &= \frac{1}{m_\text{node}} \sum_{i\in \text{node}} (\hat y_{node} - y^{(i)})^2\\[1ex] \hat y_\text{node} &= \frac{1}{m_\text{node}} \sum_{i\in\text{node}} y^{(i)} \end{align*} \end{split}\]

회귀 결정트리 규제

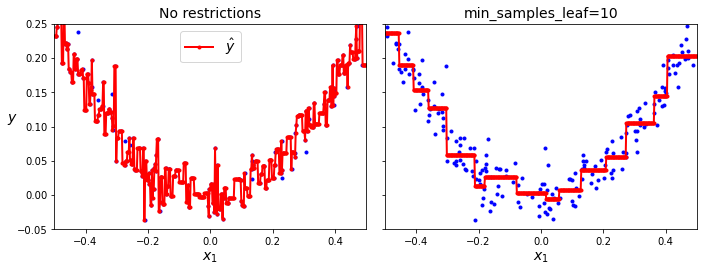
분류의 경우처럼 규제가 없으면 과대적합이 발생한다. 아래 왼쪽 그래프는 규제없이 훈련되어 훈련셋에 과대적합된 결정트리의 예측값을 보여준다. 반면에 오른쪽 그래프는 min_samples_leaf=10 규제를 사용한 결과이며, 일반화 성능이 훨씬 결정트리의 예측값을 보여준다.

6.4. 결정트리 단점#

6.4.1. 훈련셋 회전 민감도#

결정트리 알고리즘은 단순하지만 매우 뛰어난 성능을 갖지만 몇 가지 단점을 갖는다.

먼저 결정트리는 항상 축에 수직인 분할을 사용한다. 따라서 훈련셋에 회전을 조금만 가해도 결정 경계가 많이 달라진다. 예를 들어 아래 오른쪽 그래프는 왼쪽 데이터셋을 45도 회전시킨 훈련셋으로 학습된 결정트리이며 쓸데없이 계단 형식의 굴곡이 있는 결정경계를 갖는다.

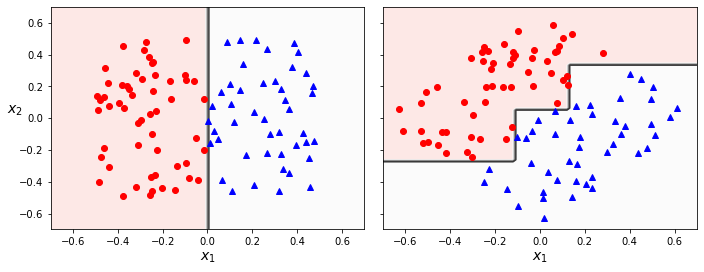
하지만 예를 들어 (8장에서 배울) 주성분 분석(PCA) 기법 등을 사용하여 훈련 샘플 회전시키는 전처리를 구행한 후에 학습을 시키는 것도 가능하다.

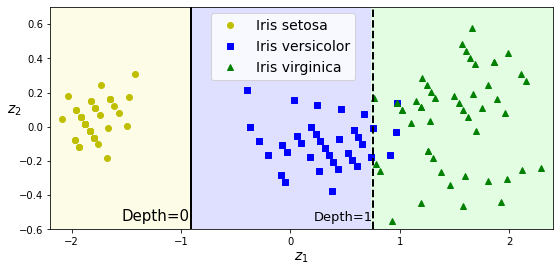
PCA 기법은 간단하게 말해 데이터셋을 회전시켜서 특성들 사이의 연관성을 약화시키며, 이를 통해 결정트리의 학습에 도움을 줄 수 있다는 정도만 여기서는 언급한다. 예를 들어, PCA 기법으로 회전시킨 붓꽃 데이터셋에 분류 결정트리를 훈련시킨 결과는 다음과 같다.

from sklearn.decomposition import PCA
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler

pca_pipeline = make_pipeline(StandardScaler(), PCA())
X_iris_rotated = pca_pipeline.fit_transform(X_iris)
tree_clf_pca = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf_pca.fit(X_iris_rotated, y_iris)

6.4.2. 높은 분산#

결정트리는 꽤 높은 분산을 갖는다. 즉, 훈련셋이나 하이퍼파라미터가 조금만 달라져도 완전히 다른 결정트리가 훈련될 수 있다. 심지어 동일한 모델을 훈련시켜도 많이 다른 결정트리가 생성되기도 한다. 이는 결정트리가 생성될 때 특성을 무작위로 선택하기 때문이다. 따라서 random_state 를 지정하지 않으면 아래 그래프와 같은 많이 다른 결정트리가 생성되기도 한다.

랜덤 포레스트

높은 분산 문제는 여러 개의 결정트리를 동시에 훈련시킨 후 평균값을 활용하는 랜덤 포레스트 모델을 이용하면 해결된다. 이에 대한 자세한 내용은 7장를 참고한다.

6.5. 연습문제#

참고: (실습) 결정트리