3. 텐서#
참고
Introduction to Tensors를 참고하였습니다.
소스코드
여기서 언급되는 코드를 (구글 코랩) 텐서에서 직접 실행할 수 있다.
슬라이드
본문 내용을 요약한 슬라이드를 다운로드할 수 있다.
주요 내용
넘파이 어레이와 텐서
텐서의 종류
텐서의 모양, 랭크, 축, 크기
텐서 연산
텐서 변환
3.1. 넘파이 어레이와 텐서#
MNIST 손글씨 데이터 분류 모델의 훈련에 사용된 훈련셋과 테스트셋은
넘파이 어레이, 즉 numpy.ndarray(이하 np.ndarray) 자료형으로 저장된다.
머신러닝에 사용되는 데이터셋은 일반적으로 넘파이 어레이와 같은
텐서tensor에 저장된다.
텐서tensor는 데이터를 담은 모음 자료형을 가리키며
넘파이 어레이가 대표적인 텐서이다.
텐서플로우 라이브러리는 자체의 Tensor 자료형인 tensorflow.Tensor(이하 tf.Tensor)를 제공한다.
tf.Tensor는 넘파이 어레이와 매우 유사하지만 GPU를 활용한 연산을 지원한다는 점에서 넘파이 어레이와 다르다.
앞서 신경망 모델을 구성할 때처럼
여기서는 tensorflow.keras를 기본 패키지로 사용하는데
케라스 신경망 모델의 입력, 출력값으로 넘파이 어레이가 기본으로 사용된다.
반면에 모델 훈련 과정을 실제로 관장하는 tensorflow의 API는 기본적으로 tf.Tensor를 모든 계산에 활용한다.
3.1.1. 넘파이 어레이의 차원#
import tensorflow as tf
import numpy as np
넘파이 어레이의 차원은 어레이 정의에 사용된 축axis의 개수로 결정되며 랭크rank라 불리기도 한다.
0차원(0D) 어레이
정수 한 개, 부동소수점 한 개 등 하나의 수를 표현하는 어레이.
스칼라scalar라고도 불림.
축이 없는 0차원 어레이임.
x0 = np.array(1.34)
y0 = np.array(12)
1차원(1D) 어레이
1열로 나열된 값들의 리스트와 같은 형식의 어레이.
벡터vector로도 불리며 한 개의 축을 가짐.
x1 = np.array([12, 3, 6, 14, 7])
2차원(2D) 어레이
행row과 열column 두 개의 축을 가짐.
행렬matrix로도 불림.
x2 = np.array([[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]])
3차원(3D) 어레이
행, 열, 깊이 세 개의 축 사용.
컬러 이미지 등을 표현할 때 사용됨.
x3 = np.array([[[5.0, 7.8, 2.1],
[6.0, 7.9, 3],
[7, 8.0, 4],
[34, 0, 3.5],
[1, 3.6, 2]],
[[5, 7.8, 2],
[3.4, 0, 3.5],
[6, 7.9, 3],
[7, 8.0, 4],
[1, 3.6, 2]]])
4차원(4D) 어레이
컬러 이미지로 구성된 데이터셋 등을 표현할 때 사용됨.
이외에 5D, 6D 어레이 등도 실전에서 활용되지만 여기서는 다루지 않는다.
벡터의 차원
벡터의 길이를 차원이라 부르기도 한다.
예를 들어, np.array([12, 3, 6, 14, 7])는 5차원 벡터다.
따라서 벡터의 차원인지, 텐서의 차원인지 명확히 구분할 필요가 있다.
3.1.2. 넘파이 어레이 주요 속성#
넘파이 어레이가 갖는 주요 특성 세 개는 다음과 같다.
ndim 속성
텐서의 차원 저장.
print(x0.ndim, x1.ndim, x2.ndim, x3.ndim, sep='\n')
0
1
2
3
shape 속성
텐서의 모양을 튜플로 저장.
각 항목은 축(axis)별로 사용된 텐서의 크기를 가리킴.
print(x0.shape, x1.shape, x2.shape, x3.shape, sep='\n')
()
(5,)
(3, 5)
(2, 5, 3)
dtype 속성
텐서에 포함된 항목의 통일된 자료형.
float16,float32,float64,int8,uint8,string등이 가장 많이 사용됨.
print(x0.dtype, x1.dtype, x2.dtype, x3.dtype, sep='\n')
float64
int64
int64
float64
3.1.3. 넘파이 어레이 실전 예제#
2D 어레이 데이터셋
각각의 샘플이 지정된 개수의 특성으로 구성된 벡터로 표현된다.
전체 데이터셋은 (샘플 수, 특성 수) 모양의 2D 텐서로 표현된다.
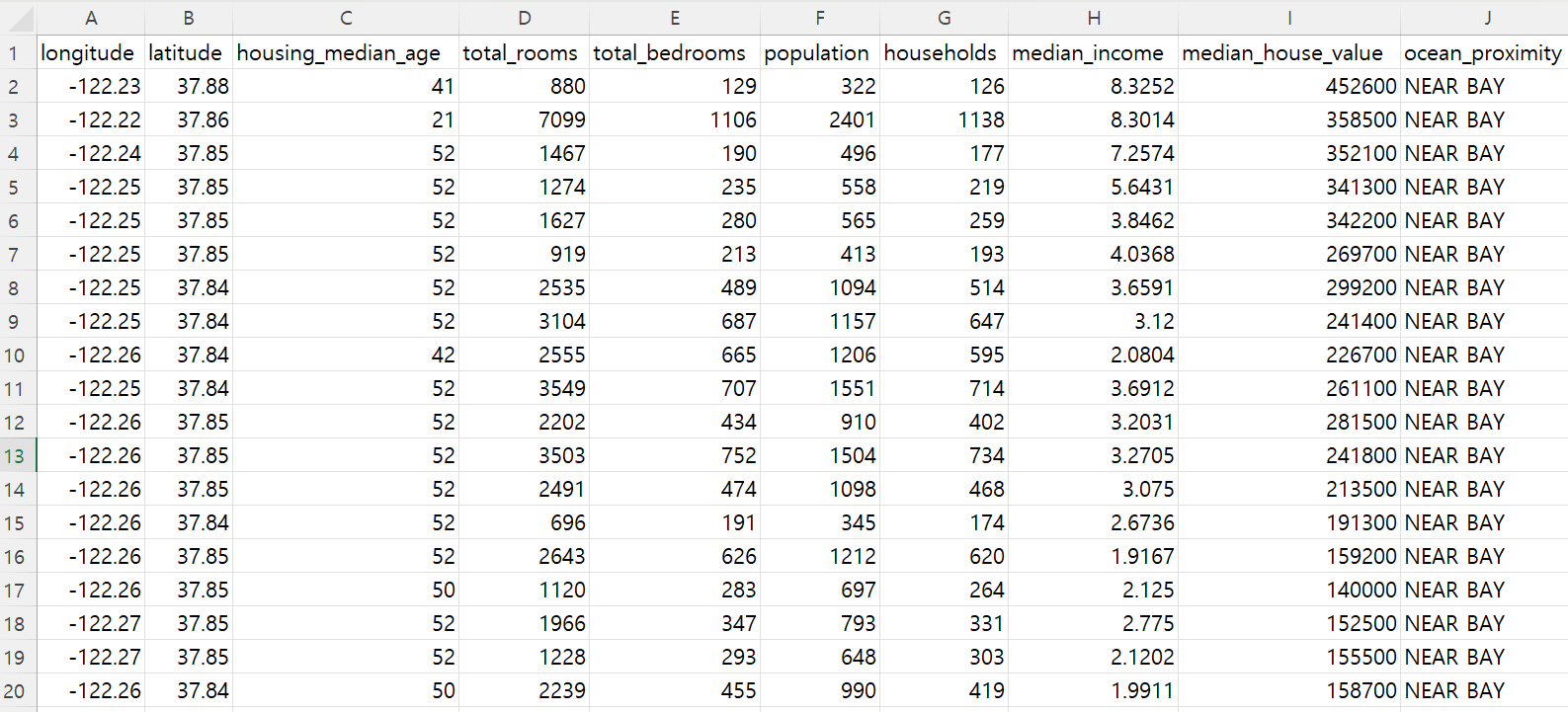
예를 들어 캘리포니아 구역별 인구조사 데이터셋이
일반적으로 2D 어레이로 제공된다.
샘플: 10개의 특성 사용. 따라서
(10,)모양의 벡터로 표현됨.데이터셋: 20,640개의 구역별 데이터 포함. 따라서
(20640, 10)모양의 2D 어레이로 표현 가능.
3D 어레이 데이터셋
흑백 손글씨 사진으로 구성된 MNIST 데이터셋이 대표적이다.
샘플:
28x28크기의 (흑백) 손글씨 사진.(28, 28)모양의 2D 텐서로 표현 가능.MNIST 훈련 데이터셋: 총 6만개의 (흑백) 손글씨 사진으로 구성됨.
(60000, 28, 28)모양의 3D 어레이로 표현 가능.
4D 텐서 실전 활용 예제
컬러 사진으로 구성된 데이터셋은
(샘플 수, 높이, 너비, 채널 수) 또는 (샘플 수, 채널 수, 높이, 너비)
모양의 4D 텐서로 표현된다.
RGB를 사용하는 컬러 어미지는 3개의 커널을, 흑백 사진은 1개의 채널을 갖는다.
예를 들어 256x256 크기의 컬러 사진 128개를 갖는 데이터셋은
(128, 256, 256, 3) 모양 4D 텐서로 표현된다.

반면에 28x28 크기의 흑백 사진 128개를 갖는 데이터셋 또는 배치는
(128, 28, 28, 1) 모양 4D 텐서로 표현된다.
하지만 MNIST의 경우처럼 흑백 사진 데이터셋은 일반적으로 3D 어레이로 표현한다.
3.2. 텐서플로우의 텐서#
텐서플로우는 두 종류의 텐서 자료형을 지원한다.
불변 텐서:
tf.Tensor자료형입출력 데이터 등 변하지 않는 값을 다룰 때 사용.
불변 자료형
가변 텐서:
tf.Variable자료형모델의 가중치, 편향 등 항목의 업데이트가 필요할 때 사용되는 텐서.
가변 자료형
사용법은 기본적으로 넘파이 어레이와 유사하며, GPU 연산과 그레이디언트 자동계산, 빅데이터 처리 등 신경망 모델 훈련에 최적화된 기능을 제공한다.
3.2.1. 불변 텐서#
불변 텐서를 다양한 방식으로 생성할 수 있다. 아래 코드는 직접 불변 텐서의 모양과 항목을 지정한다.
x = tf.constant([[1., 2.], [3., 4.]])
print(x)
tf.Tensor(
[[1. 2.]
[3. 4.]], shape=(2, 2), dtype=float32)
넘파이 어레이의 경우와 거의 유사하게 다양한 불변 텐서를 생성하는 함수들이 제공된다.
tf.ones() 함수는 1로만 이루어진 불변 텐서를 생성한다.
x = tf.ones(shape=(2, 1))
print(x)
tf.Tensor(
[[1.]
[1.]], shape=(2, 1), dtype=float32)
반면에 tf.zeros() 텐서는 0으로만 이루어진 불변 텐서를 생성한다.
x = tf.zeros(shape=(2, 1))
print(x)
tf.Tensor(
[[0.]
[0.]], shape=(2, 1), dtype=float32)
특정 확률분포를 따르는 값들로 구성된 불변 텐서를 생성하는 다음 두 함수가 딥러닝에서 매우 유용하게 활용된다. 두 함수 모두 불변 텐서를 생성한다.
normal()함수: 평균값(mean)과 표준편차(stddev)를 지정하면 해당 정규분포를 따르는 항목들을 이용하여 원하는 모양의 불변 텐서를 생성한다.
x = tf.random.normal(shape=(3, 1), mean=0., stddev=1.)
print(x)
tf.Tensor(
[[ 0.23775762]
[-1.3753685 ]
[-2.166317 ]], shape=(3, 1), dtype=float32)
uniform()함수: 지정된 구간 최솟값(minval)과 최댓값(maxval) 사이에서 균등분포를 따르는 항목들을 이용하여 불변 텐서를 생성한다.
x = tf.random.uniform(shape=(3, 1), minval=0., maxval=1.)
print(x)
tf.Tensor(
[[0.22281778]
[0.28075564]
[0.9108522 ]], shape=(3, 1), dtype=float32)
불변 텐서의 수정 불가능성
한 번 생성된 불변 텐서는 수정이 불가능하다. 예를 들어 인덱싱으로 항목을 수정할 수 없다.
x[0, 0] = 1.0
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In[14], line 1
----> 1 x[0, 0] = 1.0
TypeError: 'tensorflow.python.framework.ops.EagerTensor' object does not support item assignment
참고로 넘파이 어레이는 항상 항목 수정이 가능하다.
import numpy as np
y = np.ones(shape=(2, 2))
y[0, 0] = 0.0
print(y)
[[0. 1.]
[1. 1.]]
3.2.2. 가변 텐서#
tf.Variaible 객체는 항목을 수정할 수 있는 가변 텐서다.
아래 코드는 정규 분포를 이용하여 (3. 1) 모양의 가변 텐서를 생성한다.
v = tf.Variable(initial_value=tf.random.normal(shape=(3, 1)))
print(v)
<tf.Variable 'Variable:0' shape=(3, 1) dtype=float32, numpy=
array([[ 1.3996521 ],
[-0.91019785],
[ 0.08374712]], dtype=float32)>
가변 텐서 대체
assign() 메서드는 해당 텐서를 통째로 모양이 동일한 다른 텐서로 대체한다.
v.assign(tf.ones((3, 1)))
<tf.Variable 'UnreadVariable' shape=(3, 1) dtype=float32, numpy=
array([[1.],
[1.],
[1.]], dtype=float32)>
단, 대체하는 텐서의 모양(shape)이 기존 텐서의 모양과 동일해야 한다.
v.assign(tf.ones((3, 2)))
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[18], line 1
----> 1 v.assign(tf.ones((3, 2)))
File ~/miniconda3/lib/python3.12/site-packages/tensorflow/python/ops/weak_tensor_ops.py:142, in weak_tensor_binary_op_wrapper.<locals>.wrapper(*args, **kwargs)
140 def wrapper(*args, **kwargs):
141 if not ops.is_auto_dtype_conversion_enabled():
--> 142 return op(*args, **kwargs)
143 bound_arguments = signature.bind(*args, **kwargs)
144 bound_arguments.apply_defaults()
File ~/miniconda3/lib/python3.12/site-packages/tensorflow/python/ops/resource_variable_ops.py:1085, in BaseResourceVariable.assign(self, value, use_locking, name, read_value)
1083 else:
1084 tensor_name = " " + str(self.name)
-> 1085 raise ValueError(
1086 (f"Cannot assign value to variable '{tensor_name}': Shape mismatch."
1087 f"The variable shape {self._shape}, and the "
1088 f"assigned value shape {value_tensor.shape} are incompatible."))
1089 kwargs = {}
1090 if forward_compat.forward_compatible(2022, 3, 23):
1091 # If the shape is fully defined, we do a runtime check with the shape of
1092 # value.
ValueError: Cannot assign value to variable ' Variable:0': Shape mismatch.The variable shape (3, 1), and the assigned value shape (3, 2) are incompatible.
가변 텐서 항목 수정
가변 텐서의 특정 항목을 수정하려면 인덱싱과 assign() 메서드를 함께 사용한다.
v[0, 0].assign(3.)
<tf.Variable 'UnreadVariable' shape=(3, 1) dtype=float32, numpy=
array([[3.],
[1.],
[1.]], dtype=float32)>
assign_add()와assign_sub()
assign_sub() 메서드는 -= 연산자,
assign_add() 메서드는 += 연산자의 기능을 갖는다.
특히 assign_sub() 메서드가 경사하강법 적용과정에서 가중치와 편향 텐서를 업데이트할 때 사용된다.
v.assign_sub(tf.ones((3, 1)))
<tf.Variable 'UnreadVariable' shape=(3, 1) dtype=float32, numpy=
array([[2.],
[0.],
[0.]], dtype=float32)>
가변 텐서 활용
가변 텐서는 경상하강법으로 매 스텝마다 업데이트되어야 하는 파라미터들로 구성된 텐서로 주로 활용된다.
3.2.3. 차원과 모양#
텐서틀로우 텐서의 기본 성질과 활용법을 간단하게 살펴 본다. 불변 텐서를 이용하지만 가변 텐서에 대해서도 기본적으로 동일하게 작동한다. 텐서의 차원과 모양은 넘파이 어레이의 경우와 사실상 동일하다. 또한 두 자료형 사이의 변환이 필요에 따라 자유자재로 처리된다.
스칼라: 0차원 텐서
d0_tensor = tf.constant(4)
print(d0_tensor)
print()
print("차원:", d0_tensor.ndim)
print("모양:", d0_tensor.shape)
print("항목 자료형:", d0_tensor.dtype)
tf.Tensor(4, shape=(), dtype=int32)
차원: 0
모양: ()
항목 자료형: <dtype: 'int32'>
벡터: 1차원 텐서
d1_tensor = tf.constant([2.0, 3.0, 4.0])
print(d1_tensor)
print()
print("차원:", d1_tensor.ndim)
print("모양:", d1_tensor.shape)
print("항목 자료형:", d1_tensor.dtype)
tf.Tensor([2. 3. 4.], shape=(3,), dtype=float32)
차원: 1
모양: (3,)
항목 자료형: <dtype: 'float32'>
행렬: 2차원 텐서
아래 d2_tensor는 dtype 키워드 인자를 이용하여 자료형을 tf.int16으로 지정하였다.
d2_tensor = tf.constant([[1, 2],
[3, 4],
[5, 6]], dtype=tf.int16)
print(d2_tensor)
print()
print("차원:", d2_tensor.ndim)
print("모양:", d2_tensor.shape)
print("항목 자료형:", d2_tensor.dtype)
tf.Tensor(
[[1 2]
[3 4]
[5 6]], shape=(3, 2), dtype=int16)
차원: 2
모양: (3, 2)
항목 자료형: <dtype: 'int16'>
dtype을 지정하지 않았다면 d0_tensor의 경우처럼 int32로
dtype이 자동 지정되었을 것이다.
참고로 int32는 int16 보다 보다 큰 정수를 다룰 수 있으며
따라서 보다 많은 메모리와 계산 시간이 소비된다.
딥러닝 모델은 경우에 따라 매우 큰 텐서 연산을 실행해야 하기에
계산의 시간적, 공간적 효율성이 매우 중요하다.
따라서 반드시 필요한 만큼의 메모리를 확보하는
dtype을 지정하는 일이 중요하다.
d2_tensor = tf.constant([[1, 2],
[3, 4],
[5, 6]])
print(d2_tensor)
tf.Tensor(
[[1 2]
[3 4]
[5 6]], shape=(3, 2), dtype=int32)
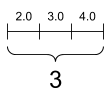
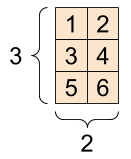
언급된 세 개의 텐서를 그림으로 나타내면 다음과 같다.
스칼라, 모양: [] |
벡터, 모양: [3] |
행렬, 모양: [3, 2] |
|---|---|---|
 |
 |
 |
3차원 텐서
세 개의 축을 사용한다.
d3_tensor = tf.constant([[[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]],
[[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]],
[[20, 21, 22, 23, 24],
[25, 26, 27, 28, 29]]
])
3차원 텐서의 모양은 다음과 같이 세 개의 축 각각에 사용된 항목의 수로 구성된 길이가 3인 리스트처럼 생겼다.
print(d3_tensor)
print()
print("차원:", d3_tensor.ndim)
print("모양:", d3_tensor.shape)
print("항목 자료형:", d3_tensor.dtype)
tf.Tensor(
[[[ 0 1 2 3 4]
[ 5 6 7 8 9]]
[[10 11 12 13 14]
[15 16 17 18 19]]
[[20 21 22 23 24]
[25 26 27 28 29]]], shape=(3, 2, 5), dtype=int32)
차원: 3
모양: (3, 2, 5)
항목 자료형: <dtype: 'int32'>
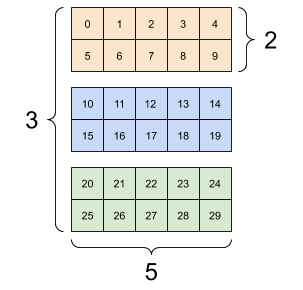
랭크-3 텐서를 여러 가지 방식으로 시각화할 수 있다.
d3_tensor의 모양: [3, 2, 5] |
||
|---|---|---|
 |
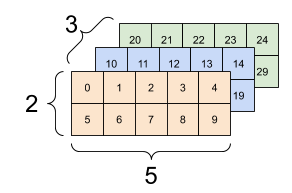 |
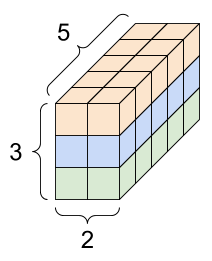 |
4차원 텐서
네 개의 축을 사용한다.
예를 들어 d4_tensor는 tf.zeros() 함수를 이용하여 생성된
모든 항목이 0인 4차원 텐서를 가리킨다.
d4_tensor = tf.zeros([3, 2, 4, 5])
print(d4_tensor)
print()
print("차원:", d4_tensor.ndim)
print("모양:", d4_tensor.shape)
print("항목 자료형:", d4_tensor.dtype)
tf.Tensor(
[[[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]]
[[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]]
[[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]]], shape=(3, 2, 4, 5), dtype=float32)
차원: 4
모양: (3, 2, 4, 5)
항목 자료형: <dtype: 'float32'>
d4_tensor를 시각화하면 다음과 같다.
아래 이미지에서 Rank는 차원을 의미한다.
| 4차원 텐서의 축과 모양 | |
|---|---|
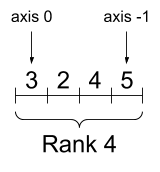 |
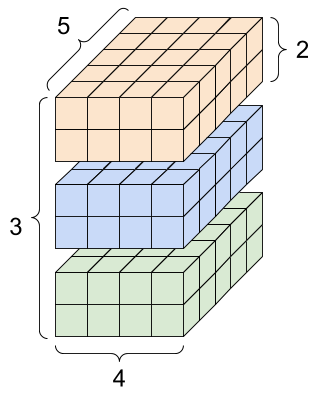 |
아래 그림은 위 4차원 텐서에 사용된 축 각각의 의미를 설명한다. 축은 텐서의 겉모양에서부터 출발하여 각각의 항목이 포함된 벡터까지 차례대로 배치batch, 높이height, 폭width, 특성features의 정보를 가리킨다.
| 축의 순서 이해 |
|---|
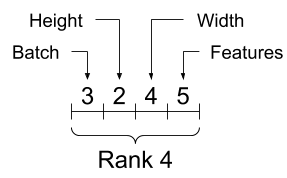 |
3.2.4. 넘파이 어레이로의 변환#
np.array() 함수 또는 tensor.numpy() 메서드를 이용하여
tf.tensor를 np.ndarray 로 변환할 수 있다.
np.array(d2_tensor)
array([[1, 2],
[3, 4],
[5, 6]], dtype=int32)
d2_tensor.numpy()
array([[1, 2],
[3, 4],
[5, 6]], dtype=int32)
3.3. 텐서 연산#
텐서의 덧셈과 곱셈은 항목별로 이루어진다.
a = tf.constant([[1, 2],
[3, 4]])
b = tf.ones([2, 2], dtype=tf.int32)
항목별 덧셈:
tf.add()함수 또는+연산자 이용
tf.add(a, b)
<tf.Tensor: shape=(2, 2), dtype=int32, numpy=
array([[2, 3],
[4, 5]], dtype=int32)>
a + b
<tf.Tensor: shape=(2, 2), dtype=int32, numpy=
array([[2, 3],
[4, 5]], dtype=int32)>
항목별 곱셈:
tf.multiply()함수 또는+연산자 이용
tf.multiply(a, b)
<tf.Tensor: shape=(2, 2), dtype=int32, numpy=
array([[1, 2],
[3, 4]], dtype=int32)>
a * b
<tf.Tensor: shape=(2, 2), dtype=int32, numpy=
array([[1, 2],
[3, 4]], dtype=int32)>
행렬(랭크-2 텐서) 연산은 항목별 연산과 다르다.
행렬 연산:
tf.matmul()함수 또는@연산자 이용
tf.matmul(a, b)
<tf.Tensor: shape=(2, 2), dtype=int32, numpy=
array([[3, 3],
[7, 7]], dtype=int32)>
a @ b
<tf.Tensor: shape=(2, 2), dtype=int32, numpy=
array([[3, 3],
[7, 7]], dtype=int32)>
이외에도 텐서는 다양한 종류의 연산에 활용된다.
c = tf.constant([[4.0, 5.0], [10.0, 1.0]])
최대 항목 찾기
tf.reduce_max(c)
<tf.Tensor: shape=(), dtype=float32, numpy=10.0>
최대 항목의 인덱스 확인
tf.math.argmax(c)
<tf.Tensor: shape=(2,), dtype=int64, numpy=array([1, 0])>
softmax()함수 적용
tf.nn.softmax(c)
<tf.Tensor: shape=(2, 2), dtype=float32, numpy=
array([[2.6894143e-01, 7.3105854e-01],
[9.9987662e-01, 1.2339458e-04]], dtype=float32)>
3.3.1. 텐서로의 자동 변환#
텐서플로우의 함수가 tf.Tensor를 인자로 입력받아야 하는데
인자가 tf.Tensor 자료형이 아니지만 텐서로 변환될 수 있으면
tf.Tensor로 자동 변환되어 처리된다.
이유는 내부적으로 tf.convert_to_tensor() 함수가
형변환을 실행하기 때문이다.
예를 들어, 리스트와 넘파이 어레이가 이에 해당한다.
tf.convert_to_tensor([1,2,3])
<tf.Tensor: shape=(3,), dtype=int32, numpy=array([1, 2, 3], dtype=int32)>
tf.reduce_max([1, 2, 3])
<tf.Tensor: shape=(), dtype=int32, numpy=3>
tf.math.argmax([1, 2, 3])
<tf.Tensor: shape=(), dtype=int64, numpy=2>
tf.nn.softmax(np.array([1.0, 12.0, 33.0]))
<tf.Tensor: shape=(3,), dtype=float64, numpy=array([1.26641655e-14, 7.58256042e-10, 9.99999999e-01])>
3.4. 텐서 인덱싱/슬라이싱#
텐서의 인덱싱과 슬라이싱 또한 넘파이의 경우와 동일하게 작동한다. 예를 들어 아래 랭크-3 텐서를 이용한 인덱싱/슬라이싱 예를 하나 살펴보자.
d3_tensor
<tf.Tensor: shape=(3, 2, 5), dtype=int32, numpy=
array([[[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9]],
[[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]],
[[20, 21, 22, 23, 24],
[25, 26, 27, 28, 29]]], dtype=int32)>
d3_tensor 텐서는 세 개의 축을 사용하는 랭크-3 텐서이며
모양은 다음과 같다.
d3_tensor.shape
TensorShape([3, 2, 5])
즉, 0번 축은 3 개의 항목을, 1번 축은 2 개의 항목을, 2번 축은 5 개의 항목을 각각 갖는다.
아래 코드는 0번 축과 1번 축의 모든 항목에 대해 2번 축의 4번 인덱스에 해당하는 값만 추출한다.
d3_tensor[:, :, 4]
<tf.Tensor: shape=(3, 2), dtype=int32, numpy=
array([[ 4, 9],
[14, 19],
[24, 29]], dtype=int32)>
| 배치에서 각 예의 모든 위치에서 마지막 특성 선택하기 | |
|---|---|
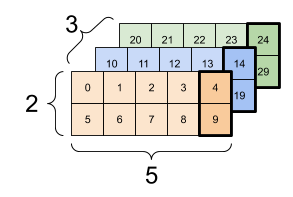 |
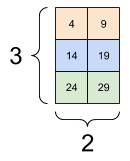 |
3.5. 텐서의 모양과 dtype 변환#
3.5.1. 모양 변환#
주어진 텐서의 모양을 변환해서 새로운 모양의 텐서를 생성할 수 있다. 단, 새로운 텐서를 위해 메모리를 더 사용하는 것은 아니며 단지 주어진 텐서의 정보를 활용하기에 매우 빠르고 메모리 효율적으로 작동한다. 이렇게 새로운 텐서를 생성하는 방식을 뷰view라 부른다.
x = tf.constant([[1], [2], [3]])
x
<tf.Tensor: shape=(3, 1), dtype=int32, numpy=
array([[1],
[2],
[3]], dtype=int32)>
x.shape
TensorShape([3, 1])
reshaped = tf.reshape(x, [1, 3])
reshaped
<tf.Tensor: shape=(1, 3), dtype=int32, numpy=array([[1, 2, 3]], dtype=int32)>
reshaped.shape
TensorShape([1, 3])
모양을 변환할 때 -1을 사용하면 그것은 해당 축의 항목의 개수는 다른 축의 항목의 개수에 맞춰서 자동으로 지정된다는 의미다. 이것이 가능한 이유는 텐서의 모양 변환을 통해 생성된 텐서는 기존의 텐서와 동일한 크기, 동일한 항목의 수를 가져야만 하기 때문이다.
예를 들어 아래 코드에서 사용된 -1은 3을 가리킨다. 이유는 총 세 개의 항목이 있는데 0번 축에 1개의 항목이 있어야 한다면 1번 축엔 세 개의 항목이 있어야 하기 때문이다.
reshaped = tf.reshape(x, [1, -1])
reshaped
<tf.Tensor: shape=(1, 3), dtype=int32, numpy=array([[1, 2, 3]], dtype=int32)>
3.5.2. dtype 변환#
tf.cast() 함수를 이용하여 dtype 속성에 저장된
항목들의 자료형을 강제로 형변환하여
새로운 텐서를 생성할 수 있다.
예제: 64비트 부동소수점 항목으로 구성된 텐서 선언
the_f64_tensor = tf.constant([2.2, 3.3, 4.4], dtype=tf.float64)
the_f64_tensor
<tf.Tensor: shape=(3,), dtype=float64, numpy=array([2.2, 3.3, 4.4])>
16비트 부동소수점 항목으로 구성된 텐서로 형변환하여 텐서 선언
the_f16_tensor = tf.cast(the_f64_tensor, dtype=tf.float16)
the_f16_tensor
<tf.Tensor: shape=(3,), dtype=float16, numpy=array([2.2, 3.3, 4.4], dtype=float16)>
8비트 음이 아닌 정수unsigned int로 구성된 텐서로 형변환
the_u8_tensor = tf.cast(the_f16_tensor, dtype=tf.uint8)
the_u8_tensor
<tf.Tensor: shape=(3,), dtype=uint8, numpy=array([2, 3, 4], dtype=uint8)>
3.5.3. 브로드캐스팅#
예를 들어 벡터에 스칼라를 더하려 하면 스칼라가 벡터와 모양을 맞춘 후 항목별 덧셈이 실행된다. 이때 새로 생성되는 벡터의 항목은 모두 스칼라로 지정된다. 이처럼 두 연산자의 모양을 자동으로 맞춘 후 연산이 실행되도록 하는 것을 브로드캐스팅broadcasting이라 하며 넘파이 어레이 연산에 적용디는 그것과 동일하게 작동한다.
x = tf.constant([1, 2, 3])
y = tf.constant(2)
z = tf.constant([2, 2, 2])
다음 세 개의 연산 결과가 모두 동일하다.
print(tf.multiply(x, 2))
print(x * y)
print(x * z)
tf.Tensor([2 4 6], shape=(3,), dtype=int32)
tf.Tensor([2 4 6], shape=(3,), dtype=int32)
tf.Tensor([2 4 6], shape=(3,), dtype=int32)
벡터와 행렬의 연산도 유사하게 작동한다.
x = tf.reshape(x,[3,1])
x
<tf.Tensor: shape=(3, 1), dtype=int32, numpy=
array([[1],
[2],
[3]], dtype=int32)>
y = tf.range(1, 5)
y
<tf.Tensor: shape=(4,), dtype=int32, numpy=array([1, 2, 3, 4], dtype=int32)>
아래 곱셈 연산은 먼저 x와 y를 모두
[3, 4] 모양의 행렬로 브로드캐스팅을 한 다음에
항목별 곱셈을 실행한다.
x * y
<tf.Tensor: shape=(3, 4), dtype=int32, numpy=
array([[ 1, 2, 3, 4],
[ 2, 4, 6, 8],
[ 3, 6, 9, 12]], dtype=int32)>
추가 시 브로드캐스팅: [1, 4]와 [3, 1]의 곱하기는 [3,4]입니다. |
|---|
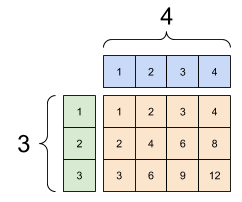 |
실제로 내부적으로 아래 연산과 동일하게 작동한다.
x_stretch = tf.constant([[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3]])
y_stretch = tf.constant([[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4]])
print(x_stretch * y_stretch)
tf.Tensor(
[[ 1 2 3 4]
[ 2 4 6 8]
[ 3 6 9 12]], shape=(3, 4), dtype=int32)
3.6. 다양한 종류의 텐서#
3.6.1. 비정형 텐서#
비정형 텐서raggedn tensor는
벡터의 길이가 일정하지 않은 축이 사용되는 텐서를 가리킨다.
tf.Tensor 자료형으로는 선언할 수 없으며
대신 tf.ragged.RaggedTensor 자료형으로 선언한다.
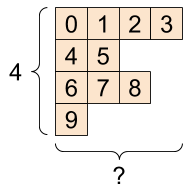
예를 들어, 아래 그림은 0번 축의 길이는 4이지만 1번 축의
길이가 일정하지 않는 비정형 텐서를 보여준다.
아래 비정형 텐서의 모양은 [4, None]으로 표시한다.
None은 해당 축에 포함된 벡터들의 길이가 일정하지 않음을 의미한다.
[4, None] 모양의 비정형 텐서 |
|---|
 |
위 그림 모양의 비정형 텐서를 선언해 보자. 이를 위해 아래 리스트를 이용한다.
ragged_list = [
[0, 1, 2, 3],
[4, 5],
[6, 7, 8],
[9]]
정규 텐서로는 선언할 수 없다.
try:
tensor = tf.constant(ragged_list)
except Exception as e:
print(f"{type(e).__name__}: {e}")
ValueError: Can't convert non-rectangular Python sequence to Tensor.
대신 tf.ragged.constant를 사용하여 tf.RaggedTensor로 선언할 수 있다.
ragged_tensor = tf.ragged.constant(ragged_list)
print(ragged_tensor)
<tf.RaggedTensor [[0, 1, 2, 3], [4, 5], [6, 7, 8], [9]]>
tf.RaggedTensor의 모양에서 축의 길이를 알 수 없는 축은 None으로 나타낸다.
print(ragged_tensor.shape)
(4, None)
3.6.2. 희소 텐서#
텐서의 크기가 매우 큰 반면에 0이 아닌 항목의 개수가 상대적으로
적을 때 희소 텐서sparse tensor를
사용하면 메모리를 보다 효율적으로 활용할 수 있다.
희소 텐서는 tf.sparse.SparseTensor 자료형이 지원한다.
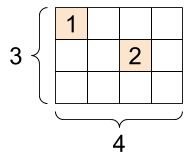
아래 그림은 [3, 4] 모양의 텐서 단 두 개의 값을 제외한 나머지는
0인 희소 텐서를 보여준다.
`tf.SparseTensor`, 모양: [3, 4] |
|---|
 |
아래 sparse_tensor 변수는 위 그림으로 표현된
희소 텐서를 가리킨다.
tf.sparse.SparseTensor 객체를 선언할 때
다음 세 개의 인자를 지정한다.
indices: 0이 아닌 항목들의 인덱스로 구성된 리스트values: 지정된 인덱스에 위치하는 항목들의 리스트dense_shape: 텐서의 모양
sparse_tensor = tf.sparse.SparseTensor(indices=[[0, 0], [1, 2]],
values=[1, 2],
dense_shape=[3, 4])
sparse_tensor
SparseTensor(indices=tf.Tensor(
[[0 0]
[1 2]], shape=(2, 2), dtype=int64), values=tf.Tensor([1 2], shape=(2,), dtype=int32), dense_shape=tf.Tensor([3 4], shape=(2,), dtype=int64))
밀집 텐서 대 희소 텐서
일반적인 텐서를 밀집 텐서dense tensor라 부른다. 텐서플로우는 내부적으로 희소 텐서와 밀집 텐서를 모두 다룰 수 있으며 필요에 따라 변환해서 사용한다.
희소 텐서를 밀집 텐서로 직접 변환하려면
tf.sparse.to_dense() 함수를 이용하면 된다.
dense_tensor = tf.sparse.to_dense(sparse_tensor)
dense_tensor
<tf.Tensor: shape=(3, 4), dtype=int32, numpy=
array([[1, 0, 0, 0],
[0, 0, 2, 0],
[0, 0, 0, 0]], dtype=int32)>
반면에 tf.sparse.from_dense() 함수는 밀집 텐서를 희소 텐서로 변환한다.
tf.sparse.from_dense(dense_tensor)
SparseTensor(indices=tf.Tensor(
[[0 0]
[1 2]], shape=(2, 2), dtype=int64), values=tf.Tensor([1 2], shape=(2,), dtype=int32), dense_shape=tf.Tensor([3 4], shape=(2,), dtype=int64))