출처: 위키백과
참고: 여기서 사용하는 코드는 조엘 그루스(Joel Grus)의 밑다닥부터 시작하는 데이터 과학 4장에 사용된 소스코드의 일부를 기반으로 작성되었다.
선형대수는 벡터와 행렬의 성질을 연구하는 수학의 한 분야이다.
여기서는 데이터 분석 기술의 핵심 자료형인 넘파이 어레이(numpy.array)의 개념과
기능에 기초를 제공하는 벡터와 행렬의 기본 개념을 소개한다.
넘파이 어레이(numpy.array)는 길이와 모양에 대한 정보와 함께 어레이를 조작하거나
어레이로부터 다양한 정보를 추출하는 메서드를 기본으로 제공한다.
반면에 파이썬 리스트(list)는 인덱싱과 몇 개의 리스트 조작 기능 이외에
별 다른 정보와 기능을 제공하지 않는다.
여기서는 벡터와 행렬을 각각 1차원과 2차원 리스트로 구현하여 실용적으로 사용하는 과정을 살펴본다. 보다 구체적으로는 벡터와 행렬의 자료형 정의에서 출발하여 벡터와 행렬의 연산 등을 모두 리스트와 기본 파이썬만을 이용하여 구현한다.
이를 통해 넘파이 어레이가 제공하는 다양한 기능에 대한 보다 깊은 이해와 함께 파이썬 데이터 분석 관련 프로그래밍 실력 향상에 도움을 주고자 한다.
주의사항: 아래 코드는 자료형 명시(type annotation)와 리스트 조건제시법을 많이 활용한다.
벡터는 유한 개의 숫자를 담고 있으며, 벡터의 길이를 차원(dimension)이라 부른다.
주의사항: 넘파이 어레이의 차원과 다른 개념임에 주의하라.
벡터는 수학과 통계에서 많이 사용된다.
수학 예제: 2차원 평면 공간에서 방향과 크기를 표현하는 2차원 벡터 (x, y)
통계 예제: 사람들의 키, 몸무게, 나이로 이루어진 3차원 벡터 (키, 몸무게, 나이)
통계 예제: 네 번의 시험 점수로 이루어진 4차원 벡터 (1차점수, 2차점수, 3차점수, 4차점수)
벡터 자료형은 부동소수점들로 이루어진 리스트로 정의될 수 있다.
from typing import List
Vector = List[float]
# (키, 몸무게, 나이)
height_weight_age1 : Vector = [70, 170, 50]
height_weight_age2 : Vector = [66, 163, 50]
# (1차점수, 2차점수, 3차점수, 4차점수)
grades1 : Vector = [95, 80, 75, 62]
grades2 : Vector = [85, 82, 79, 82]
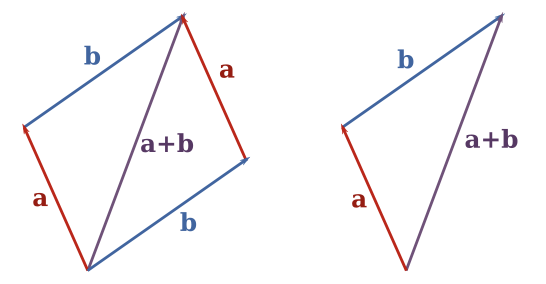
차원이 같은 벡터 두 개의 덧셈은 같은 위치에 있는 항목끼기 더한 결과로 이루어진 벡터를 생성한다.
벡터 $a$와 벡터 $b$의 합 $a+b$의 의미를 아래 그래프에서처럼 해석할 수 있다.

출처: 위키백과
차원이 같은 두 벡터의 항목별 합을 항목으로 같은 벡터를 반환하는 함수는 다음과 같다.
def addV(v: Vector, w: Vector) -> Vector:
assert len(v) == len(w) # 두 벡터의 길이가 같아야 함
return [v_i + w_i for v_i, w_i in zip(v, w)]
addV(height_weight_age1, height_weight_age2)
[136, 333, 100]
addV(grades1, grades2)
[180, 162, 154, 144]
동일한 차원의 임의의 개수의 벡터를 더하는 함수를 다음과 같이 정의할 수 있다.
def vector_sum(vectors: List[Vector]) -> Vector:
"""
인자: 동일한 차원의 벡터들의 리스트
반환값: 각 항목의 합으로 이루어진 동일한 차원의 벡터
"""
assert vectors # 1개 이상의 벡터가 주어져야 함
num_elements = len(vectors[0]) # 벡터 개수
assert all(len(v) == num_elements for v in vectors) # 모든 벡터의 크기가 같아야 함
# 동일한 위치의 항목을 모두 더한 값들로 이루어진 벡터 반환
return [sum(vector[i] for vector in vectors)
for i in range(num_elements)]
예를 들어, 2차원 벡터 네 개를 더한 결과는 다음과 같다.
vector_sum([[1, 2], [3, 4], [5, 6], [7, 8]])
[16, 20]
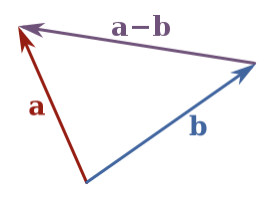
차원이 같은 벡터 두 개의 덧셈은 같은 위치에 있는 항목끼기 뺀 결과로 이루어진 벡터를 생성한다.
벡터 $a$와 벡터 $b$의 합 $a-b$의 의미를 아래 그래프에서처럼 해석할 수 있다.
출처: 위키백과
차원이 같은 두 벡터의 항목별 차를 항목으로 같은 벡터를 반환하는 함수는 다음과 같다.
def subtractV(v: Vector, w: Vector) -> Vector:
assert len(v) == len(w) # 두 벡터의 길이가 같아야 함
return [v_i - w_i for v_i, w_i in zip(v, w)]
subtractV(height_weight_age1, height_weight_age2)
[4, 7, 0]
subtractV(grades1, grades2)
[10, -2, -4, -20]
숫자 하나와 벡터의 곱셈을 스칼라 곱셈이라 부른다. 스칼라 곱셈은 벡터의 각 항목을 지정된 숫자로 곱해 새로운 벡터를 생성한다.
벡터의 각 항목에 동일한 부동소수점을 곱한 결과를 반화하는 함수는 다음과 같다.
def scalar_multV(c: float, v: Vector) -> Vector:
return [c * v_i for v_i in v]
scalar_multV(2, [1, 2, 3])
[2, 4, 6]
동일한 차원의 여러 벡터가 주어졌을 때 항목별 평균을 구할 수 있다. 항목별 평균은 항목끼리 모두 더한 후 벡터의 개수로 나눈다. 따라서 벡터의 덧셈과 스칼라 곱셈을 이용할 수 있다.
동일한 차원의 여러 벡터가 주어졌을 때 항목별 평균으로 이루어진 벡터를 반환하는 함수는 다음과 같다.
def vector_mean(vectors: List[Vector]) -> Vector:
n = len(vectors)
return scalar_multV(1/n, vector_sum(vectors))
참고: 5/3은 약 1.666666이다.
vector_mean([[1, 2], [2, 1], [2, 3]])
[1.6666666666666665, 2.0]
차원이 같은 벡터 두 개의 내적은 같은 위치에 있는 항목끼기 곱한 후 모두 더한 값이다. 벡터 $u = (u_1, \cdots, u_n)$와 벡터 $v = (v_1, \cdots, v_n)$가 주어졌을 때 두 벡터의 내적은 아래와 같다.
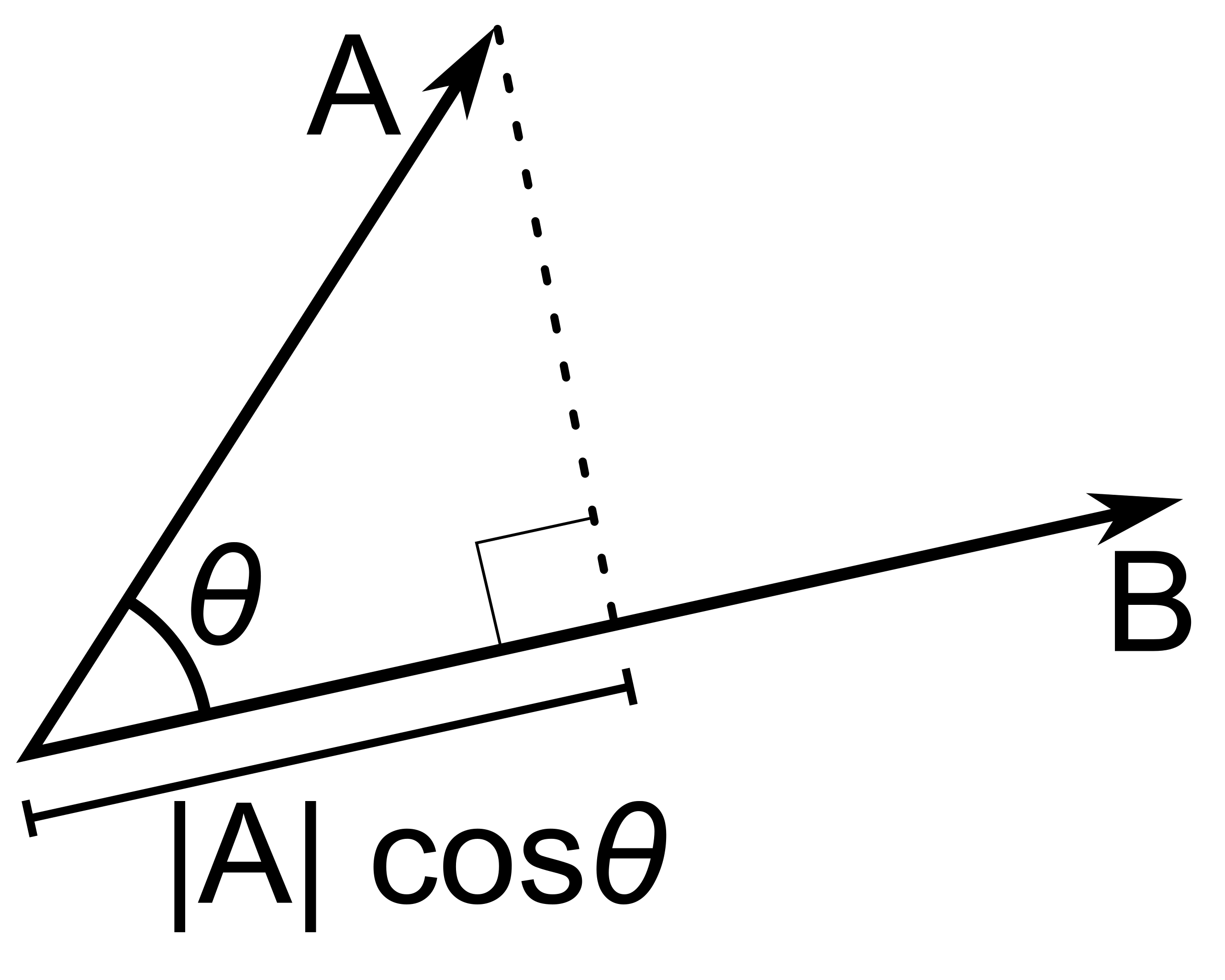
$$ \begin{align*} u \cdot v &= \sum_{i=1}^n u_i\cdot v_i \\ &= u_1\cdot v_1 + \cdots + u_n\cdot v_n \end{align*} $$두 개의 벡터 $A$와 $B$가 주어졌고, 벡터 $B$의 길이가 1이라고 가정하자. 그러면 내적 $A \cdot B$는 벡터 $A$가 벡터 $B$ 방향으로 사영되었을 때의 길이를 나타낸다.
출처: 위키백과
임의의 벡터 $B$에 대한 내적 $A \cdot B$는 다음과 같다. ($\theta$ 두 벡터가 이루는 각을 나타낸다.)
$$ A \cdot B = \vert A\vert\cdot \vert B\vert \cdot \cos\theta $$동일 차원의 두 벡터의 내적을 반환하는 함수는 다음과 같다.
def dot(v: Vector, w: Vector) -> float:
assert len(v) == len(w), "벡터들의 길이가 동일해야 함"""
return sum(v_i * w_i for v_i, w_i in zip(v, w))
dot([1, 2, 3], [4, 5, 6]) == 32
True
벡터 $v = (v_1, \cdots, v_n)$가 주어졌을 때 각 항목별 제곱의 합은 $v$와 $v$ 자신의 내적과 같다.
$$v \cdot v = v_1^2 + \cdots + v_n^2$$그런데 이 값은 정확하게 벡터 $v$의 크기 $\vert v\vert$의 제곱이다. 따라서 다음이 성립한다.
$$\vert v\vert = \sqrt{v \cdot v} = \sqrt{v_1^2 + \cdots + v_n^2}$$예를 들어 벡터 $(3, 4)$의 크기는 다음과 같다.
import math
def sum_of_squares(v: Vector) -> float:
return dot(v, v)
def magnitude(v: Vector) -> float:
return math.sqrt(sum_of_squares(v))
magnitude([3, 4])
5.0
벡터 $v = (v_1, \cdots, v_n)$와 벡터 $w = (w_1, \cdots, w_n)$ 사이의 거리는 벡터 $v-w$의 크기, 즉 아래처럼 정의된 $\vert v - w \vert$이다.
$$ \begin{align*} \vert v - w\vert &= \sqrt{(v-w) \cdot (v-w)} \\[.5ex] &= \sqrt{(v_1-w_1)^2 + \cdots + (v_n-w_n)^2} \end{align*} $$예를 들어, 두 벡터 $(1, 2)$와 $(2, 1)$ 사이의 거리는 다음과 같다.
def squared_distance(v: Vector, w: Vector) -> float:
return sum_of_squares(subtractV(v, w))
# 버전 1
def distance(v: Vector, w: Vector) -> float:
return math.sqrt(squared_distance(v, w))
# 버전 2
def distance(v: Vector, w: Vector) -> float:
return magnitude(subtractV(v, w))
참고: $\sqrt{2} = 1.41421356237...$
distance([1,2], [2,1])
1.4142135623730951
행렬(matrix)은 보통 숫자들을 직사각형 형태로 배열한 것이다.
예를 들어, $1, 2, 3, 4, 5, 6$ 여섯 개의 항목을 가진 행렬의 모양(shape)은 네 종류가 있다. 이유는 6을 두 개의 양의 정수의 곱셈으로 표현하는 방법이 네 가지이기 때문이다.
$$ 6 = 1\times6 = 2\times 3 = 3 \times 2 = 6 \times 1$$행렬을 리스트의 리스트, 즉 2중 리스트로 구현한다.
Matrix = List[List[float]]
예를 들어, 아래 A와 B는 각각 (2, 3), (3, 2) 모양의 행렬을 나타낸다.
A = [[1, 2, 3], # 2 x 3 행렬
[4, 5, 6]]
B = [[1, 2], # 3 x 2 행렬
[3, 4],
[5, 6]]
$n$ 개의 행과 $k$ 개의 열로 구성된 행렬을 $n \times k$ 행렬이라 부르며,
$(n,k)$를 해당 행렬의 모양(shape)라 부른다.
아래 함수 shape()는 주어진 행렬의 모양을 튜플로 반환한다.
from typing import Tuple
def shape(A: Matrix) -> Tuple[int, int]:
num_rows = len(A)
num_cols = len(A[0]) if A else 0 # number of elements in first row
return num_rows, num_cols
shape(A)
(2, 3)
shape(B)
(3, 2)
아래 두 함수는 각각 지정된 행와 지정된 열의 항목들로 구성된 행벡터와 열벡터를 반환한다.
# 행벡터 계산
def get_row(A: Matrix, i: int) -> Vector:
return A[i]
# 열벡터 계산
def get_column(A: Matrix, j: int) -> Vector:
return [A_i[j] for A_i in A]
행렬 A의 0번 행은 다음과 같다.
get_row(A, 0)
[1, 2, 3]
행렬 B의 1번 열은 다음과 같다.
get_column(B, 1)
[2, 4, 6]
아래 함수는 지정된 모양의 행렬을 생성한다. 셋째 인자는 지정된 위치의 항목을 계산하는 함수이다.
num_rows: 행의 수num_rows: 열의 수entry_fn: i, j가 주어지면 i행, j열에 위치한 값 계산from typing import Callable
def make_matrix(num_rows: int,
num_cols: int,
entry_fn: Callable[[int, int], float]) -> Matrix:
return [ [entry_fn(i, j) for j in range(num_cols)] for i in range(num_rows)]
영행렬(zero matrix)이란 행렬의 모든 원소의 값이 0인 행렬을 말한다. 예를 들어 아래 행렬은 (3, 2) 모양의 영행렬이다.
$$ \begin{bmatrix} 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{bmatrix} $$지정된 모양의 영행렬을 생성하는 함수는 다음과 같다.
def zero_matrix(n: int, m:int) -> Matrix:
return make_matrix(n, m, lambda i, j: 0)
zero_matrix(5,7)
[[0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0]]
단위행렬(identity matrix)은 정사각형 모양의 행렬 중에서 대각선 상에 위치한 항목은 1이고 나머지는 0인 행렬을 말한다. 예를 들어 아래 행렬은 (5, 5) 모양의 단위행렬이다.
\begin{bmatrix} 1&0&0&0&0 \\ 0&1&0&0&0 \\ 0&0&1&0&0 \\ 0&0&0&1&0 \\ 0&0&0&0&1 \end{bmatrix}단위행렬은 행과 열의 개수가 동일한 정방행렬이며, 지정된 모양의 단위행렬을 생성하는 함수는 다음과 같다.
def identity_matrix(n: int) -> Matrix:
return make_matrix(n, n, lambda i, j: 1 if i == j else 0)
identity_matrix(5)
[[1, 0, 0, 0, 0], [0, 1, 0, 0, 0], [0, 0, 1, 0, 0], [0, 0, 0, 1, 0], [0, 0, 0, 0, 1]]
모양이 같은 두 행렬의 덧셈/뺄셈은 항목별로 더한/뺀 결과로 이루어진 행렬이다. 즉, 벡터의 덧셈/뺄셈과 동일한 방식이다. 예를 들어, $2 \times 3$ 행렬의 덧셈/뺄셈은 다음과 같다.
행렬의 덧셈과 뺄셈을 계산하는 함수는 다음과 같다.
def addM(A: Matrix, B: Matrix) -> Matrix:
assert shape(A) == shape(B)
m, n = shape(A)
return make_matrix(m, n, lambda i, j: A[i][j] + B[i][j])
def subtractM(A: Matrix, B: Matrix) -> Matrix:
assert shape(A) == shape(B)
m, n = shape(A)
return make_matrix(m, n, lambda i, j: A[i][j] - B[i][j])
C = [[1, 3, 7],
[1, 0, 0]]
D = [[0, 0, 5],
[7, 5, 0]]
addM(C, D)
[[1, 3, 12], [8, 5, 0]]
subtractM(C, D)
[[1, 3, 2], [-6, -5, 0]]
숫자 하나와 행렬의 곱셈을 행렬 스칼라 곱셈이라 부른다. 스칼라 곱셈은 행렬의 각 항목을 지정된 숫자로 곱해 새로운 행렬을 생성한다. 즉, 벡터의 스칼라 곱셈과 동일한 방식이다.
예를 들어, (2, 3) 모양의 행렬의 스칼라 곱셈은 다음과 같다.
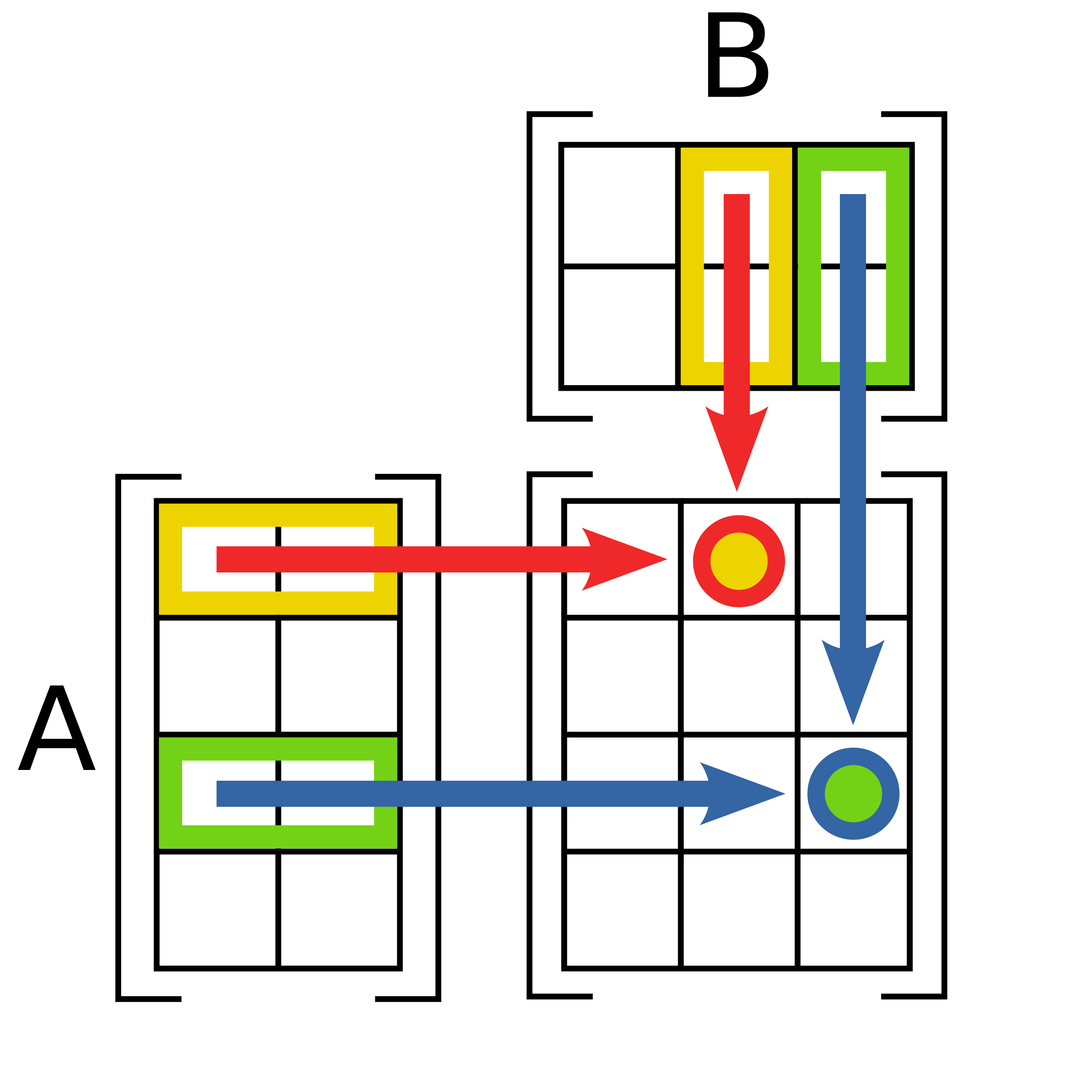
$$ \begin{align*} 2\cdot \begin{bmatrix}1&8&-3\\4&-2&5\end{bmatrix} &= \begin{bmatrix}2\cdot 1&2\cdot 8&2\cdot -3\\2\cdot 4&2\cdot -2&2\cdot 5\end{bmatrix} \\[.5ex] &= \begin{bmatrix}2&16&-6\\8&-4&10\end{bmatrix} \end{align*} $$$m \times n$ 행렬 $A$와 $n \times p$ 행렬 $B$의 곱은 $m \times p$ 행렬이며, 각 $(i, j)$번째 항목은 다음과 같이 정의된다.
그림으로 나타내면 다음과 같다.
출처: 위키백과
즉, 좌측 행렬 열의 수 $n$과 우측 행렬 행의 수 $n$이 같은 경우에만 곱셈이 가능하다. 예를 들어, $2 \times 3$ 행렬과 $3 \times 2$ 행렬의 곱셈은 다음과 같다.
$$ \begin{align*} \begin{bmatrix} 1&0&2\\-1&3&1 \end{bmatrix} \begin{bmatrix} 3&1\\2&1\\1&0 \end{bmatrix} &= \begin{bmatrix} (1\cdot 3+0\cdot 2+2\cdot 1)&(1\cdot 1+0\cdot 1+2\cdot 0)\\(-1\cdot 3+3\cdot 2+1\cdot 1)&(-1\cdot 1+3\cdot 1+1\cdot 0) \end{bmatrix} \\[.5ex] &= \begin{bmatrix} 5&1\\4&2 \end{bmatrix} \end{align*} $$행렬 $A B$의 $(i, j)$번째 항목 $(A B)_{ij}$는 벡터 내적과 깊이 연관되어 있다.
먼저, $m \times n$ 행렬 $A$와 $n \times p$ 행렬 $B$의 곱 $A \times B$의 $(i, j)$ 번째 항목은 다음과 같다.
반면에 행렬 $A$의 $i$ 행벡터를
$$A^0_i = (A_{i0},\dots, A_{i(n-1)}),$$행렬 $B$의 $j$ 열벡터를
$$B^1_j = (B_{0j},\dots, B_{(n-1)j})$$라 할 때, 다음이 성립한다.
$$ A^0_i \cdot B^1_j = A_{i0} \cdot B_{0j} + A_{i2} \cdot B_{2j} + \cdots + A_{i(n-1)} \cdot B_{(n-1)j} $$즉, $(A B)_{ij}$는 $A$의 $i$ 행벡터와 $B$의 $j$ 열벡터의 내적으로 정의된다.
예를 들어 $2 \times 3$ 행렬과 $3 \times 2$ 행렬의 곱셈을 다시 살펴보자.
위 계산을 벡터 내적으로 표현해보자. 먼저 두 행렬 $A$와 $B$를 지정한다.
그러면
$$(A\cdot B)_{11} = -1\cdot 1+3\cdot 1+1\cdot 0 = 2$$이고, 이것은 아래 결과와 동일하다.
영행렬은 행렬 덧셈의 항등원이며, 단위행렬은 행렬 곱셈의 항등원이다.
행렬의 전치란 행과 열을 바꾸는 것으로, 행렬 $A$의 전치는 $A^T$로 나타낸다. 즉, $A$가 $m \times n$ 행렬이면 $A^T$는 $n \times m$ 행렬이며, 그리고 $A^T$의 $i$행의 $j$열번째 값은 $A$의 $j$행의 $i$열번째 값이다. 즉,
$$ A ^{T}_{ij} = A_{ji} $$예를 들어, $2\times 3$ 행렬의 전치는 $3 \times 2$ 행렬이 되며 다음과 같이 작동한다.
$$ \begin{bmatrix} 9&8&7\\ -1&3&4 \end{bmatrix}^{T} = \begin{bmatrix} 9&-1\\ 8&3\\ 7&4 \end{bmatrix} $$$a$를 스칼라, $A, B$를 크기가 같은 행렬이라 하자. 이때 다음이 성립한다.
행렬의 스칼라 곱셈을 실행하는 함수 scalar_multM() 를 구현하라.
# pass와 None 적절한 코드와 표현식으로 대체하라.
def scalar_multM(c: float, A: Matrix) -> Matrix:
pass
return None
행렬 곱셈을 실행하는 함수 multM() 를 구현하라.
# pass와 None 적절한 코드와 표현식으로 대체하라.
# 힌트: 벡터 내적을 이용하라.
def multM(A: Matrix, B: Matrix) -> Matrix:
pass
return None
아래 행렬을 이용하여 아래 assert 명령문이 성립함을 확인하라.
E = [[3, 1],
[2, 1],
[1, 0]]
assert addM(E, zero_matrix(3, 2)) == E
assert multM(E, identity_matrix(2)) == E
전치 행렬을 생성하는 함수 transpose() 를 구현하라.
# pass와 None 적절한 코드와 표현식으로 대체하라.
def transpose(A: Matrix) -> Matrix:
pass
return None
앞서 정의된 행렬 A, B, C, D를 이용하여 전치행렬의 성질 5개가 성립함을 보여라.
assert transpose(transpost(A)) == A
assert transpose(addM(C, D)) == addM(transpose(C), transpose(D))
assert transpose(subtractM(C, D)) == subtractM(transpose(C), transpose(D))
assert transpose(scalar_multM(3, A)) == scalar_multM(3, transpose(A))
assert transpose(multM(A, B)) == multM(transpose(B), transpose(A))
어떤 동호회의 사용자 아이디 $i$와 $j$가 친구사이라는 사실을 $(i, j)$로 표시한다고 하자. 그리고 열 명의 사용자 사이의 친구관계가 다음과 같다고 가정하자.
friendships = [(0, 1), (0, 2), (1, 2), (1, 3), (2, 3), (3, 4),
(4, 5), (5, 6), (5, 7), (6, 8), (7, 8), (8, 9)]
그런데 이렇게 하면 사용자들 사이의 친구관계를 쉽게 파악하기 어렵다. 반면에 아래와 같이 $10\times 10$ 행렬로 표시하면 다르게 보인다.
즉, 사용자 $i$와 사용자 $j$ 사이의 친구관계 성립여부는 행렬 $F$의 $(i,j)$ 번째 항목이 1이면 친구관계이고, 0이면 아니라는 것을 바로 확인할 수 있다. 즉, $F_{ij} = 1$인가를 확인만 하면 된다.
위 행렬 $F$를 구현하는 (10, 10) 모양의 행렬를 가리키는 변수 friend_matrix 를 선언하라.
# None 을 적절한 표현식으로 대체하라.
friend_matrix = None
아이디 0번은 아이디 2번과 친구관계이다.
assert friend_matrix[0][2] == 1
아이디 8번은 아이디 0번과 친구관계가 아니다.
assert friend_matrix[8][0] == 0
아이디 5번과 친구사이인 아이디는 다음과 같다.
friends_of_five = [ i for i, is_friend in enumerate(friend_matrix[5]) if is_friend ]
friends_of_five
본문 포함 앞서 정의한 함수를 모두 넘파이 어레이를 이용하여 구현하라.
주의사항: 넘파이의 linalg 모듈 등 추가 모듈은 절대 사용하지 못한다.
문제 5에서 정의한 함수를 모두 넘파이의 linalg 모듈에서
제공하는 함수로 대체하라.
넘파이의 linalg 모듈에서
제공하는 pinv() 함수를 예를 들어 설명하라.