(부록) 재귀 함수

20. (부록) 재귀 함수#

하나의 함수가 실행되는 동안 다른 함수를 호출할 수 있으며 심지어 실행되는 함수 자신을 다시 호출할 수 있다. 예를 들어 아래 countdown() 함수의 본문에 현재 정의되고 있는 자신에 대한 호출이 포함되어 있다.

def countdown(n):
    if n <= 0:
        print('발사!')
    else:
        print(n)
        countdown(n-1)

countdown() 함수의 작동 방식은 다음과 같다.

  • n 이 0 이하인 경우: '발사!' 출력

  • n 이 양의 정수인 경우: n을 출력한 다음 바로 countdown(n-1) 호출.

n 이 양수인 경우 동일한 함수가 호출되지만 인자가 1적어 지고 결국 n이 되어 더 이상의 함수 호출이 없어 실행이 멈춘다. 예를 들어 countdown(3)을 호출하면 다음처럼 실행된다.

countdown(3)

3
2
1
발사!

함수 본문에 자신을 호출하는 함수를 기능을 재귀recursion라 하며, 재귀 함수recursive function는 재귀를 활용하는 함수이다.

20.1. 기저 조건과 무한 재귀#

재귀 함수의 실행이 멈추려면 재귀 호출 과정에서 언젠가는 더 이상 자신을 호출하지 않아야 한다. countdown() 함수는 0과 함께 호출될 때 더 이상 재귀 호출을 하지 않는다. 이렇게 더 이상 재귀 호출이 발생하지 않도록 하는 경우를 기저 조건base case이라 한다. 즉, countdown() 함수의 기저 조건은 n = 0이다.

반면에 아래 함수는 기저 조건을 갖지 않는다.

def count_infinitely(n):
    print(n)
    count_finitely(n+1)

count_infinitely() 함수를 호출하면 재귀 호출이 무한정 반복됨을 쉽게 알 수 있다. 하지만 파이썬을 포함해서 대부분의 프로그래밍 언어는 재귀 호출의 무한 반복을 허용하지 않고 언젠가 아래와 같은 오류를 발생시키면서 실행을 중지시킨다.

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<stdin>", line 3, in count_infinitely
  File "<stdin>", line 3, in count_infinitely
  File "<stdin>", line 3, in count_infinitely
  [Previous line repeated 992 more times]
  File "<stdin>", line 2, in count_infinitely
RecursionError: maximum recursion depth exceeded while calling a Python object

최대 재귀 한도

파이썬은 최대 재귀 한도Maximum recursion depth를 정해 허용되는 재귀 호출의 최대 반복 횟수를 지정한다. 한도는 파이썬 버전과 운영체제 등에 따라 다를 수 있으며 필요에 따라 조정하는 것도 가능하다.

사용하는 파이썬의 최대 재귀 한도는 다음 명령문으로 확인할 수 있다.

>>> import sys
>>> print(sys.getrecursionlimit())

재귀 함수를 실행해서 무한 반복에 빠지거나 최대 재귀 한도를 벗어났다는 오류 메시지가 발생하면 다음 두 가지 사항을 확인해야 한다.

  • 기저 조건이 주어졌는가?

  • 어떠한 경우에도 기저 조건에 다달하는가?

하나라도 충족되지 않거나 확인할 수 없다면 해당 재귀 함수의 활용에 매우 주의를 기울여야 한다.

20.2. 재귀 함수의 반환값#

함수의 반환값을 지정하는 return 표현식이 여러 번 사용될 수 있다. 예를 들어 짝수이면 0, 홀수이면 1을 반환하는 함수는 다음과 같이 정의한다.

def even_odd(n):
    if n % 2 == 0:
        return 0
    else:
        return 1

even_odd(8)

0

even_odd(3)

1

파이썬 프로그램은 함수 실행 중에 return 표현식 명령문을 만나면 표현식의 값을 반환하면서 동시에 함수의 실행을 멈춘다. 따라서 함수 본문에 return 명령문이 여러 번 사용되었다 하더라도 한 번만 실행되며, 결국 하나의 반환값만 지정된다. 재귀 함수에 대해서도 동일하게 적용되며 보통은 기저 조건이 성립할 때의 반환값과 재귀 단계에서의 리턴값을 별도로 지정한다.

다음 countdown_num() 함수는 카운트 다운 횟수를 반환한다. 인자로 0을 사용하면 바로 0을 반환값으로 지정하고 이후 명령문을 더 이상 실행하지 않고 바로 종료한다.

def countdown_num(n):
    if n <= 0:
        return 0
    else:
        print(n, '이(가) 양수인 경우!')
        result = countdown_num(n-1) + 1
        return result

print('반환값:', countdown_num(0))

반환값: 0

하지만 n이 0보다 크면 countdown_num(n-1) 이 재귀적으로 호출되어 실행이 종료할 때까지 기다렸다가 반환값을 받아 result가 가리키는 값을 지정한다. 이런 방식으로 재귀 과정에서 반환된 값을 받아 새로운 값을 생성하는 데에 활용할 수 있다.

예를들어 n = 1이면 재귀 호출이 한 번 발생하며 재귀 호출된 countdown_num(0)은 0을 반환하며 종료된다. 따라서 result = 0 + 1이 실행되어 최종적으로 1을 반환한다.

print('반환값:', countdown_num(1))

1 이(가) 양수인 경우!
반환값: 1

일반적으로 n = k이면 재귀 호출이 k-1 번 발생하며 재귀적으로 호출된 역순으로 계산된 값을 반환하며 실행을 종료한다.

print('반환값:', countdown_num(2))

2 이(가) 양수인 경우!
1 이(가) 양수인 경우!
반환값: 2

print('반환값:', countdown_num(3))

3 이(가) 양수인 경우!
2 이(가) 양수인 경우!
1 이(가) 양수인 경우!
반환값: 3

20.3. 재귀 함수의 콜 스택#

파이썬 프로그램의 실행은 기본적으로 “위에서 아래로”와 “왼쪽에서 오른쪽으로”의 두 기준으로 더 이상 실행할 명령문이 없을 때까지 진행된다.

그런데 프로그램 실행 도중에 함수 호출이 발생하면 함수의 실행이 종료될 때까지 이후 명령문은 대기한다. 함수 호출은 프로그램 실행 도중에 발생하는 일종의 “나들이”이다. 즉, 프로그램 실행 도중 잠시 일을 멈추고 다른 일을 먼저 완료하는 기능이며 나들이 도중에 얻어진 결과물을 이어서 활용할 수 있다.

물론 함수 본문에서 다른 함수를 호출할 수도 있기 때문에 프로그램의 실행은 무한정 복잡해질 수 있다. 다행히도 파이썬 해석기가 프로그램의 실행 과정을 철저하게 추적하고 관리한다.

프레임

함수가 실행되는 동안 발생하는 모든 정보는 컴퓨터 메모리 상에서 프레임frame 형식으로 관리된다. 프레임은 하나의 함수가 실행되는 동안 발생하는 지역 변수의 생성 및 값 할당, 할당된 값 업데이트 등을 관리한다. 함수의 실행과 함께 스택stack 메모리 영역에서 생성된 프레임은 함수의 실행이 종료되면 스택에서 사라진다. 하지만 함수의 반환값은 지정된 변수에 할당되거나 다른 함수의 인자로 전달된다.

다음 코드를 이용하여 함수 호출과 프레임 생성 및 사멸의 관계를 알아보자.

def hour2min(hour):
    min = hour * 60
    return min

def hour2sec(hour):
    min = hour2min(hour)
    sec = 60 * min
    return sec

print("2 시간은", hour2sec(2), "초입니다.")

2 시간은 7200 초입니다.

아래 그림은 hour2sec(2)가 실행되면 이어서 바로 hour2min(2)가 호출되어 hour와 min 두 지역 변수로 구성된 프레임이 포함된 콜 스택의 상태를 보여준다.

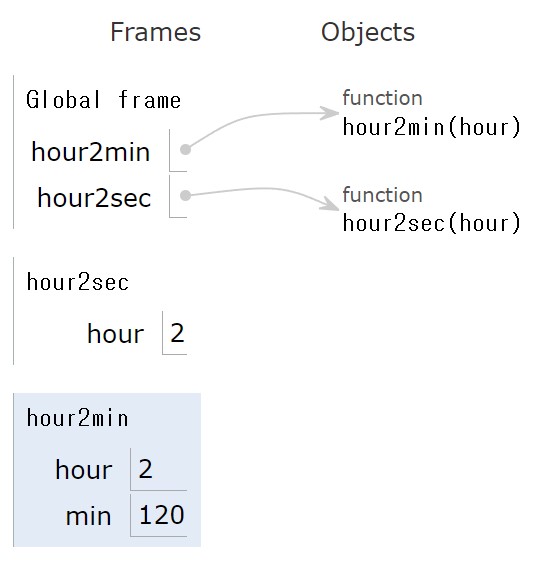
  • 맨 위 프레임: Global frame은 전역적global으로 사용 가능한 함수 이름과 전역 변수를 관리한다.

  • 가운데 프레임: hour2sec 프레임은 hour2sec() 함수가 호출되면서 생성된 프레임이며, 매개 변수 hour가 지역 변수로 포함되어 있다.

  • 맨 아래 프레임: hour2min 프레임은 변수 할당문 min = hour2min(hour)를 실행하면 먼저 hour2min() 함수가 호출되기에 새로 생성된 프레임이다. 매개 변수 hour와 지역 변수 min이 포함된다.

  • hour2sec 프레임의 지역 변수 sec은 hour2min(hour) 의 반환값이 정해지면 그때 포함된다.

위 코드의 전체 실행 과정을 PythonTutor: 프레임의 생성과 사멸에서 확인해 보면 함수 호출이 발생할 때마다 프레임이 생성되고 또 함수의 실행이 완료될 때마다 해당 함수의 프레임이 사멸하는 것을 확인할 수 있다.

콜 스택

프레임은 생성된 순서 역순으로 사멸한다. 즉, 가장 나중에 생성된 프레임이 가장 먼저, 가장 먼저 생성된 프레임이 가장 나중에 사멸한다. 이렇게 작동하는 구조가 스택stack 이기에 함수의 프레임으로 구성된 스택을 콜 스택call stack이라 부른다. 스택 다이어그램(stack diagram)은 콜 스택의 변화를 다이어그램으로 표현한다. 위 프로그램의 실행 과정에서의 스택 다이어그램의 변화는 다음과 같다.

  • 프레임 생성 순서

Global frame => hour2sec 프레임 => hour2min 프레임

  • 프레임 사멸 순서

hour2min 프레임 => hour2sec 프레임 => Global frame

재귀 함수의 실행과정 동안 많은 프레임의 생성과 소멸이 발생하여 콜 스택의 변화가 경우에 따라 매우 복잡해지기도 한다. 아래 그림은 countdown(3)을 호출했을 때의 콜 스택의 상태를 스택 다이어그램으로 보여준다.

Example 20.1 (PythonTutor: 콜라츠 추측)

PythonTutor: 콜라츠 추측에서 재귀 함수 호출 과정 동안 메모리에서 벌어지는 프레임의 생성과 소멸 과정, 즉, 콜 스택의 변화를 살펴볼 수 있다.

20.4. 재귀 함수 예제#

20.4.1. 리스트 합#

리스트 [1, 3, 5, 7, 9]에 포함된 수들의 합을 구해보자. 먼저, for 반복문을 이용하면 다음과 같다.

  • 합을 0으로 시작.

  • 각 항목을 확인하여 합에 더하기

def list_sum(num_list):
    the_sum = 0
    for i in num_list:
        the_sum = the_sum + i
    return the_sum

print(list_sum([1, 3, 5, 7, 9]))

25

위 코드의 for 반복문에서 항목을 확인할 때마다 업데이트되는 the_sum 변수는 아래 괄호가 묶인 순서대로 계산되는 값을 차례대로 가리킨다.

\[(((1 + 3) + 5) + 7) + 9\]

그런데 이 경우 재귀를 이용하려면 아래와 같이 작동하는 항목의 합을 사용해야 한다.

\[1 + (3 + (5 + (7 + 9)))\]

위 방식을 for 반복문으로 구현하면 다음과 같다.

def list_sum(num_list):
    the_sum = 0
    for i in num_list[::-1]:
        the_sum = the_sum + i
    return the_sum

print(list_sum([1, 3, 5, 7, 9]))

25

항목 더하기 문제를 재귀로 해결하려면 먼저 the_sum이 구해지는 과정을 역추적해야 한다.

\[\begin{split} \begin{align*} \text{the_sum} & = 1 + (3 + (5 + (7 + 9))) \\ \text{the_sum} & = 3 + (5 + (7 + 9)) \\ \text{the_sum} & = 5 + (7 + 9) \\ \text{the_sum} & = 7 + 9 \\ \text{the_sum} & = 9 \end{align*} \end{split}\]

the_sum의 값이 업데이트되는 과정을 번호를 붙히면 다음을 얻는다.

\[\begin{split} \begin{align*} \text{the_sum}_5 & = 1 + \text{the_sum}_4 \\ \text{the_sum}_4 & = 3 + \text{the_sum}_3 \\ \text{the_sum}_3 & = 5 + \text{the_sum}_2 \\ \text{the_sum}_2 & = 7 + \text{the_sum}_1 \\ \text{the_sum}_1 & = 9 \end{align*} \end{split}\]

리스트의 머리와 꼬리 활용

\(\text{the_sum}_{i}\)가 결정되는 방식은 모든 \(i\)에 대해 동일하게 아래 형식을 따른다.

list_sum(num_list) = num_list[0] + list_sum(num_list[1:])

위 식을 리스트의 머리와 꼬리 개념으로 이해하면 재귀 알고리즘의 작동과정을 보다 쉽게 이해할 수 있다. 단, 큐(queue)에 사용되는 머리, 꼬리 개념과 다름에 주의해야 한다.

  • 머리(head): 리스트의 0번 인덱스 값, 즉 num_list[0]

  • 꼬리(tail): 0번 인덱스를 제외한 나머지, 즉 num_list[1:]

현재 리스트에 포함된 항목의 합을 구하려면 먼저 꼬리에 재귀를 적용한 다음 얻어진 결과에 머리를 더하면 된다. 이는 꼬리에 대한 재귀가 특정 값을 반환할 때까지 머리와의 합은 대기상태로 머물러야 함을 의미한다(아래 그림 참조).

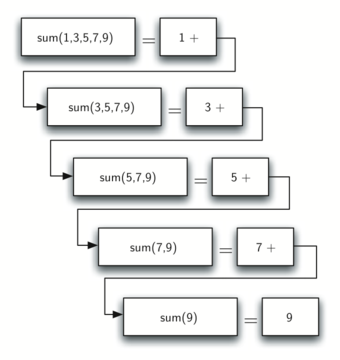
앞서 설명한 재귀를 함수로 구현하면 다음과 같다.

def list_sum(num_list):
    if len(num_list) == 1:  # 항목이 1개 일때
        return num_list[0]
    else:                   # 항목이 2개 이상일 때
        return num_list[0] + list_sum(num_list[1:])

print(list_sum([1, 3, 5, 7, 9]))

25

20.4.2. 계승#

음이 아닌 정수 \(n\)이 주어졌을 때 1부터 \(n\) 까지의 곱을 \(n\)의 계승 또는 팩토리얼factorial이라 하고 \(n!\)로 표시한다.

\[\begin{split} \begin{align*} 0! & = 1 \\ n! & = n \, (n-1)!\quad\text{단, $n>0$.} \end{align*} \end{split}\]

계승을 계산하는 함수 factorial() 을 재귀로 구현할 수 있다.

  • 기저 조건은 n == 0이고, 1을 반환한다.

  • n이 0보다 크면 (n-1)의 계승과 n을 곱합 값을 반환한다.

def factorial(n):
    if n == 0:                            # 기저 조건
        return 1
    else:
        recursion_step = factorial(n-1)   # (n-1)의 계승
        result = n * recursion_step
        return result

20.4.3. 피보나치 수열#

피보나치 수열Fibonacci sequence은 처음엔 1과 1로 시작한 후에 이후의 항목은 이전 두 개의 항목의 합으로 생성된다.

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

피보나치 수열의 두 항목의 관계 점화식은 다음과 같다.

\[\begin{split} \begin{align*} f_0 & = 1 \\ f_1 & = 1 \\ f_n & = f_{n-1} + f_{n-2} \quad \text{단, $n \ge 2$.} \end{align*} \end{split}\]

점화식이 알려진 수열의 \(n\) 번째 항목을 생성하는 함수는 기본적으로 재귀로 쉽게 구현할 수 있다. 피보나치 수열의 n 번째 값을 구하는 함수는 다음과 같다.

def fibonacci(n):
    if n == 0:
        return 1
    elif  n == 1:
        return 1
    else:                                        # n >= 2 인 경우
        return fibonacci(n-1) + fibonacci(n-2)

피보나치 수열의 처음 10개 항목은 다음과 같다.

for n in range(10):
    print(fibonacci(n), end=', ')

print('...')

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

인덱스의 시작

프로그래밍에서는 관습적으로 순서를 1번부터가 아닌 0번부터 시작한다. 따라서 피보나치 수열의 0번과 1번 값이 1, 2번 값은 2, 3번 값은 3 등이 된다.

20.4.4. 콜라츠 추측#

독일 수학자 콜라츠(Collatz -> L.)가 1937년에 아래 알고리즘을 얼마나 많이 반복하면 최종적으로 숫자 1에 다다를 것인가를 질문했다.

  • 주어진 숫자가 짝수면 2로 나눈다.

  • 주어진 숫자가 홀수면 3배한 후 1을 더한다.

실제로 숫자 7부터 시작해서 위 과정을 16번 반복하면 1에 다다른다.

7 -> 22 -> 11 -> 34 -> 17 -> 52 -> 26 -> 13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1

반면에 숫자 128부터 시작하면 7번만 반복하면 된다.

128 -> 64 -> 32 -> 16 -> 8 -> 4 -> 2 -> 1

콜라츠 알고리즘을 재귀 함수로 구현할 수 있다.

  • 기저 조건: num == 1

  • num % 2 == 0: 짝수인 경우. 2로 나누기

  • 기타else: 홀수 인 경우. 3배 더하기 1.

def collatz(num):
    if num == 1:                        # 기저 조건
        print(1)
    elif num%2 == 0:                  # 짝수인 경우
        print(num, end=' -> ')
        collatz(num//2)
    else:                               # 홀수인 경우
        print(num, end=' -> ')
        collatz(num*3 + 1)

collatz(7)

7 -> 22 -> 11 -> 34 -> 17 -> 52 -> 26 -> 13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1

collatz(128)

128 -> 64 -> 32 -> 16 -> 8 -> 4 -> 2 -> 1

collatz(129)

129 -> 388 -> 194 -> 97 -> 292 -> 146 -> 73 -> 220 -> 110 -> 55 -> 166 -> 83 -> 250 -> 125 -> 376 -> 188 -> 94 -> 47 -> 142 -> 71 -> 214 -> 107 -> 322 -> 161 -> 484 -> 242 -> 121 -> 364 -> 182 -> 91 -> 274 -> 137 -> 412 -> 206 -> 103 -> 310 -> 155 -> 466 -> 233 -> 700 -> 350 -> 175 -> 526 -> 263 -> 790 -> 395 -> 1186 -> 593 -> 1780 -> 890 -> 445 -> 1336 -> 668 -> 334 -> 167 -> 502 -> 251 -> 754 -> 377 -> 1132 -> 566 -> 283 -> 850 -> 425 -> 1276 -> 638 -> 319 -> 958 -> 479 -> 1438 -> 719 -> 2158 -> 1079 -> 3238 -> 1619 -> 4858 -> 2429 -> 7288 -> 3644 -> 1822 -> 911 -> 2734 -> 1367 -> 4102 -> 2051 -> 6154 -> 3077 -> 9232 -> 4616 -> 2308 -> 1154 -> 577 -> 1732 -> 866 -> 433 -> 1300 -> 650 -> 325 -> 976 -> 488 -> 244 -> 122 -> 61 -> 184 -> 92 -> 46 -> 23 -> 70 -> 35 -> 106 -> 53 -> 160 -> 80 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1

재귀 호출 횟수를 반환값으로 지정할 수 있다.

  • n == 1: 재귀 호출 없음. 0 반환.

  • 짝수인 경우: 2로 나눈 값에 대한 재귀 호출 횟수 더하기 1

  • 홀수인 경우: 세 배 더하기 1에 대한 재귀 호출 횟수 더하기 1

def collatz_count(num):
    if num == 1:                        # 기저 조건
        return 0
    elif num % 2 == 0:                  # 짝수인 경우
        return collatz_count(num//2) + 1
    else:                               # 홀수인 경우
        return collatz_count(num*3 + 1) + 1

print(collatz_count(7), "회")

16 회

print(collatz_count(128), "회")

7 회

print(collatz_count(129), "회")

121 회

앞서 보았듯이 처음 시작하는 값이 작다고 해서 반드시 먼저 끝나는 것이 아니다. 이처럼 시작 값이 정해졌을 때 언제 1에 다다르며 종료하는지 알려지지 않았다. 반면에 지금까지 테스트한 모든 자연수에 대해 콜라츠 알고리즘은 언젠가는 1에 다다르며 종료하였다. 즉, 콜라츠 알고리즘이 모든 수에 대해 언젠가는 1에 다다르며 정지한다라는 주장이 아직 증명도 부정도 되지 않고 있다. 이렇게 증명도 부정되 되지 않은 콜라츠의 주장을 콜라츠 추측Collatz conjecture 이라 부른다.

20.4.5. 하노이의 탑#

for, while 반복문을 이용하여 해결하기 어려운 문제를 재귀 알고리즘으로 상대적으로 훨씬 간단하게 해결하는 예제로 하노이의 탑 문제를 다룬다.

하노이의 탑Tower of Hanoi 문제는 세 개의 기둥 중에 하나의 기둥에 쌓여 있는 다양한 크기의 원판들을 다른 기둥으로 옮기는 게임이다. 단, 원판 이동 중에 아래 제한조건들을 반드시 지켜야 한다.

  • 한 번에 한개의 원판만 옮긴다.

  • 큰 원판이 그보다 작은 원판 위에 위치할 수 없다.

<그림 출처: 위키백과: 하노이의 탑>

참고: 일반적으로 원판이 \(n\)개 일 때, \(2^n - 1\)번의 이동으로 원판을 모두 옮길 수 있다. 참고로 64개의 원판을 옮기는 데 총 \(2^{64}-1\) 번 원판을 움직여야 하고, 1초에 하나의 원판을 옮긴다고 가정했을 때 5,849억년 정도 걸린다.

재귀 알고리즘

4개의 원판을 옮겨야 한다고 가정하자. 아래 연속된 그림에서 볼 수 있듯이 3개의 원판을 옮기는 과정을 두 번 반복하면 된다.

위 설명을 임의의 양의 정수 n에 대해 일반화하면 다음과 같다.

  1. n-1 개의 원판을 중간 지점의 위치에 옮긴다.

  2. 가장 큰 원판을 목적지로 옮긴다.

  3. 중간 지점에 위치한 n-1 개의 원판을 목적지로 옮긴다.

위 재귀 알고리즘의 종료조건은 n=1일 때이며, 이때는 하나의 원판을 목적지로 옮기기만 하면 된다. 이를 코드로 구현하면 다음과 같다.

  • height: 원판 개수

  • from_pole: 출발 기둥

  • with_pole: 중간 지점 기둥

  • to_pole: 목적지 기둥

def move_tower(height, from_pole, to_pole, with_pole):
    if height >= 1:
        move_tower(height - 1, from_pole, with_pole, to_pole)
        move_disk(from_pole, to_pole)                           # 탑 원판 옮기기
        move_tower(height - 1, with_pole, to_pole, from_pole)

def move_disk(from_p, to_p):
    print(f"{from_p}에서 {to_p}로 탑 원판 옮기기")

move_tower(4, "A", "B", "C")

A에서 C로 탑 원판 옮기기
A에서 B로 탑 원판 옮기기
C에서 B로 탑 원판 옮기기
A에서 C로 탑 원판 옮기기
B에서 A로 탑 원판 옮기기
B에서 C로 탑 원판 옮기기
A에서 C로 탑 원판 옮기기
A에서 B로 탑 원판 옮기기
C에서 B로 탑 원판 옮기기
C에서 A로 탑 원판 옮기기
B에서 A로 탑 원판 옮기기
C에서 B로 탑 원판 옮기기
A에서 C로 탑 원판 옮기기
A에서 B로 탑 원판 옮기기
C에서 B로 탑 원판 옮기기

머리와 꼬리

하노이의 탑 알고리즘에서 머리와 꼬리는 다음과 같다.

  • 머리: 바닥에 위치한 원판. 지정된 목적지로 이동하면 끝.

  • 꼬리: 머리를 제외한 나머지 원판으로 이루어진 탑. 따라서 하나의 꼬리에 대한 두 번의 재귀호출이 이뤄짐.

20.5. 재귀 시각화#

재귀를 이해하기 위해 재귀 알고리즘의 작동과정을 시각화 해보자. 시각화를 위해 turtle 모듈을 이용한다.

20.5.1. 소용돌이#

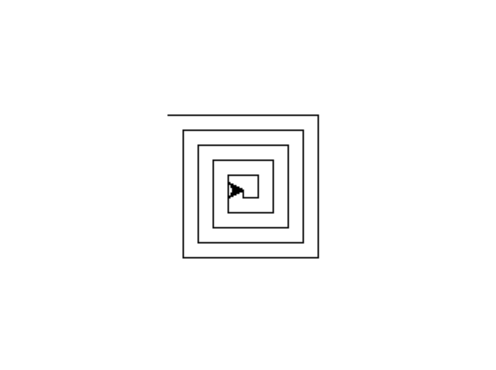
재귀로 정의된 draw_spiral() 함수는 아래 그림과 같은 소용돌이를 그린다.

import turtle

def draw_spiral(my_turtle, line_len):
    if line_len > 0:
        my_turtle.forward(line_len)
        my_turtle.right(90)
        draw_spiral(my_turtle, line_len - 5)


my_turtle = turtle.Turtle()
my_win = turtle.Screen()
draw_spiral(my_turtle, 100)
my_win.exitonclick()

20.5.2. 프랙탈 트리#

아래 이미지처럼 아무리 확대하더라도 항상 동일한 구조를 보여주는 사물이 프랙탈fractal이다.

<그림 출처: YouTube: 만델브로트 프랙탈 줌>

프랙탈의 구조는 재귀와 매우 밀접한 관계를 갖는다. 예를 들어, tree() 함수는 아래 모양의 프랙탈 트리를 그린다.

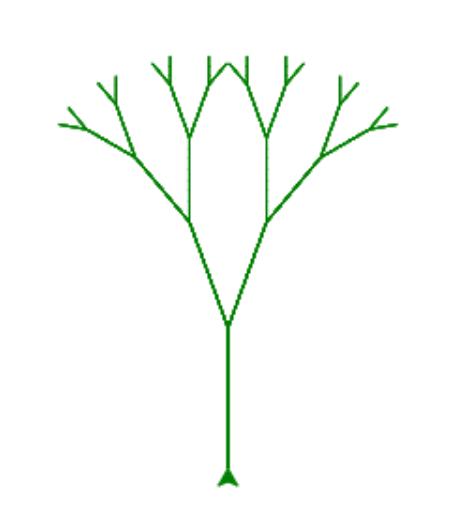
프랙탈 트리

아래 코드를 Repl.it: 프랙탈 트리에서 실행할 수 있다.

import turtle
# import time                    # 주의: repl.it 사이트에서 오류 발생

def tree(branch_len, t):
    if branch_len >= 15:           # 종료조건: branch_len < 15
        t.forward(branch_len)    # 전진
        # time.sleep(1)          
        t.right(20)              # 오른쪽 가지치기
        tree(branch_len - 15, t)
        t.left(40)               # 왼쪽 가지치기
        tree(branch_len - 15, t)
        t.right(20)              # 한 단계 후진
        t.backward(branch_len)

t = turtle.Turtle()
my_win = turtle.Screen()
t.left(90)
t.up()
t.backward(100)
t.down()
t.color("green")
tree(75, t)
my_win.exitonclick()

tree() 함수는 오른쪽 가지를 먼저 그리며, 이 과정을 최대한 멀리 진행한다. 가지치기를 할 때마다 가지의 길이를 15씩 줄이며, 그려야 할 가지의 길이가 15 미만일 때 가지치기를 멈춘다. 아래 이미지는 가지의 길이를 처음에 75로 시작해서 5번 오른쪽 가지치기를 수행한 후 더 이상의 가지치기가 불가능한 상태를 보여준다.

더 이상 오른쪽 가지치기가 불가능하면 뒤로 한 단계 후진한 다음에 왼쪽 가지치기를 진행한다. 왼쪽 가지치기 이후 오른쪽 가지치가 가능하면 이를 먼저 수행한다. 아래 이미지는 그려야할 프랙탈 트리의 절반을 그린 상태를 보여준다.

머리와 꼬리

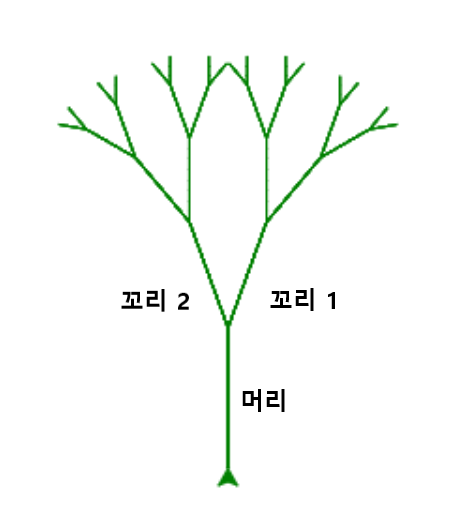
프랙탈 트리의 경우 가지 하나를 그린 다음 가지치기가 이루어지며 가지치기 이후에는 동일한 과정이 반복된다. 다만, 좌우 각 가지에서 완성되는 프랙탈 트리는 완성되어야 하는 전체 프랙탈 트리의 일부분을 담당한다. 그려진 하나의 가지를 머리, 그려져야 하는 좌우 두 개의 가지를 두 개의 꼬리로 이해할 수 있다. 즉, 아래 그림이 보여주는 것처럼 머리를 그린 다음에 나머지는 각각의 꼬리에 동일한 과제를 떠넘기는 과정의 연속이 된다.

20.6. 연습문제#

참고: (실습) 재귀 함수

Contents