9장 비지도학습

감사의 글

자료를 공개한 저자 오렐리앙 제롱과 강의자료를 지원한 한빛아카데미에게 진심어린 감사를 전합니다.

주요 내용

• 군집/군집화

• k-평균

• DBSCAN

• 가우시안 혼합

비지도 학습이란?

• 레이블이 없는 데이터 학습
  • 예제: 사진에 포함된 사람들 분류하기

• 용도
  • 군집화(clustering)
  • 이상치 탐지
  • 데이터 밀도 추정

군집화

• 비슷한 샘플끼리 군집 형성하기

• 활용 예제
  • 데이터 분석
  • 고객분류
  • 추천 시스템
  • 검색 엔진
  • 이미지 분할
  • 차원 축소
  • 준지도 학습

이상치 탐지

• 정상테이터 학습 후 이상치 탐지.

• 활용 예제
  • 제조라인에서 결함제품 탐지
  • 시계열데이터에서 새로운 트렌드 찾기

데이터 밀도 추정

• 데이터셋의 확률밀도함수 추정 가능

• 활용 예제:
  • 이상치 분류: 밀도가 낮은 지역에 위치한 샘플
  • 데이터분석
  • 시각화

9.1 군집 군집화

• 군집(클러스터, cluster): 유사한 샘플들의 모음(집합, 그룹)

• 군집화(클러스터링, clustering): 유사한 부류의 대상들로 이루어진 군집 만들기

분류 대 군집화

• 유사점: 각 샘플에 하나의 그룹 할당

• 차이점: 군집화는 군집이 미리 레이블(타깃)로 지정되지 않고 예측기 스스로 적절한 군집을 찾아내야 함.

• 예제: 분류(왼편)와 군집화(오른편)

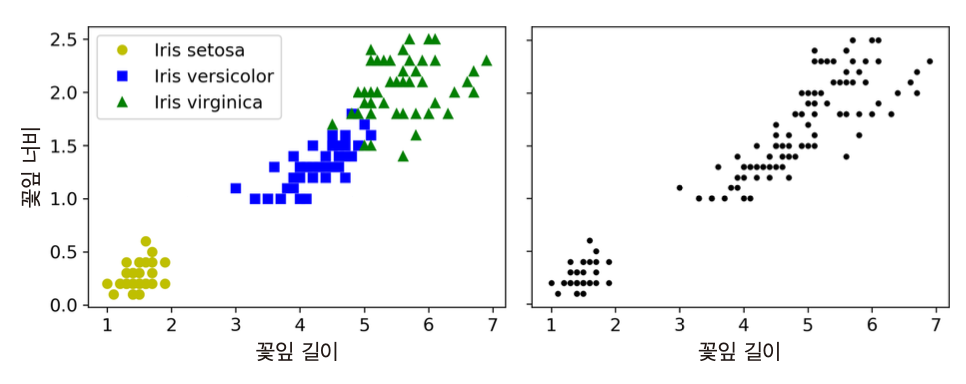
• 가우시안 혼합 모델을 적용하면 매우 정확한 군집화 가능. 단, 꽃잎의 너비/길이, 꽃받침의 너비/길이 모두 특성으로 사용해야 함.

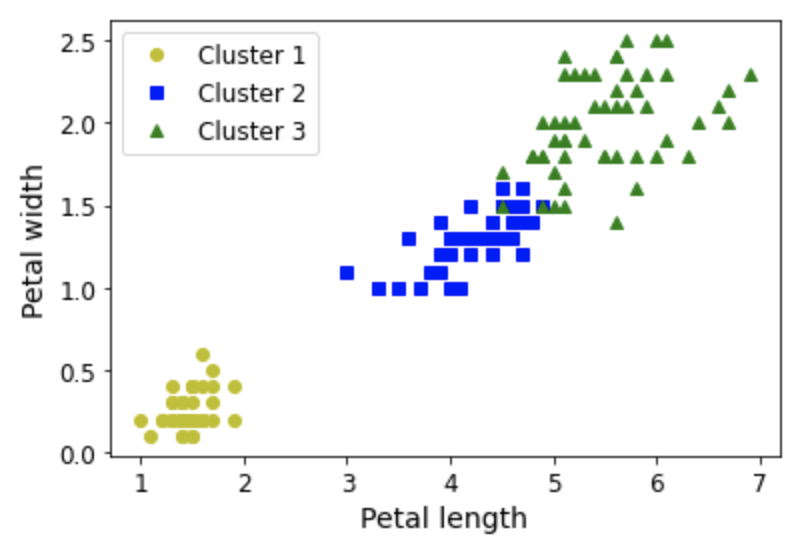
군집의 정의

• 보편적 정의 없음. 사용되는 알고리즘에 따라 다른 형식으로 군집 형성

• k-평균: 센트로이드(중심)라는 특정 샘플을 중심으로 모인 샘플들의 집합

• DBSCAN: 밀집된 샘플들의 연속으로 이루어진 집합

• 가우시안 혼합: 특정 가우시안 분포를 따르는 샘플들의 집합

k-평균

• 각 군집의 중심을 찾고 가장 가까운 군집에 샘플 할당

• 군집수(n_clusters) 지정해야 함.

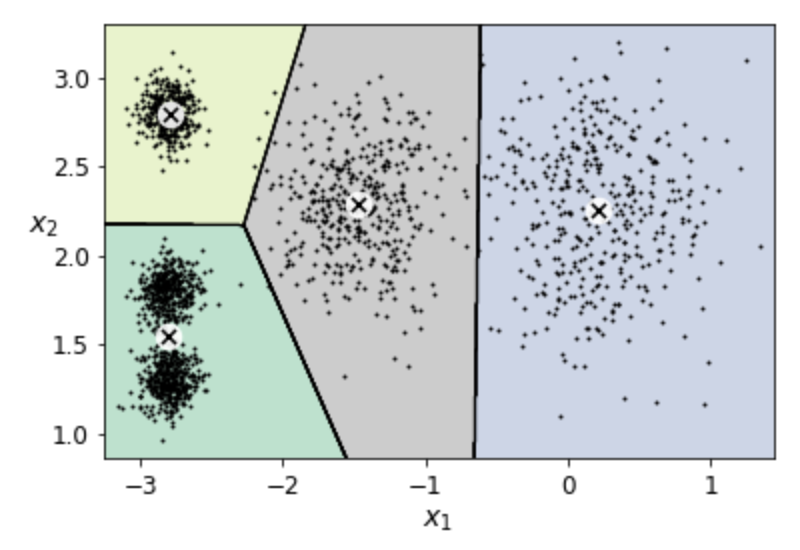
결정 경계

• 예제: 샘플 덩어리 다섯 개로 이루어진 데이터셋

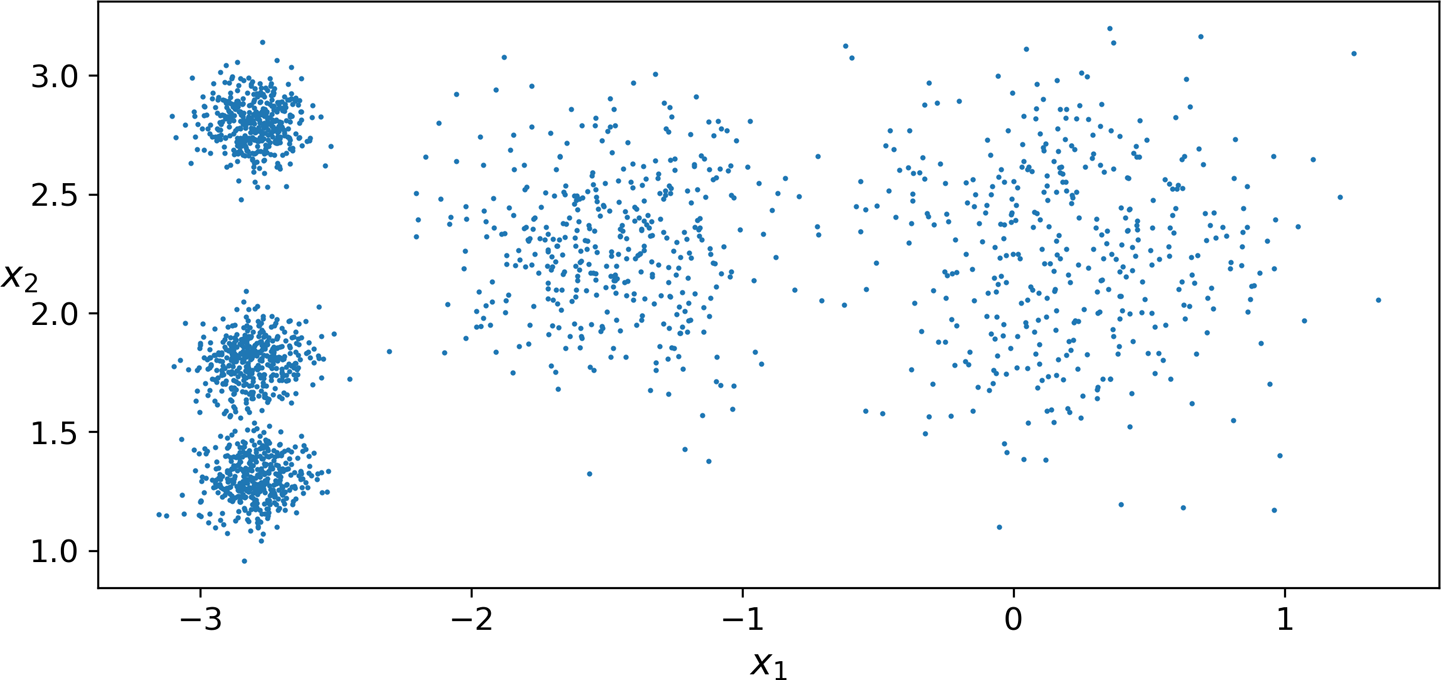
from sklearn.cluster import KMeans

k = 5
kmeans = KMeans(n_clusters=k, random_state=42)
y_pred = kmeans.fit_predict(X)

보로노이 다이어그램

• 평면을 특정 점까지의 거리가 가장 가까운 점의 집합으로 분할한 그림

• 경계 부분의 일부 샘플을 제외하고 기본적으로 군집이 잘 구성됨.

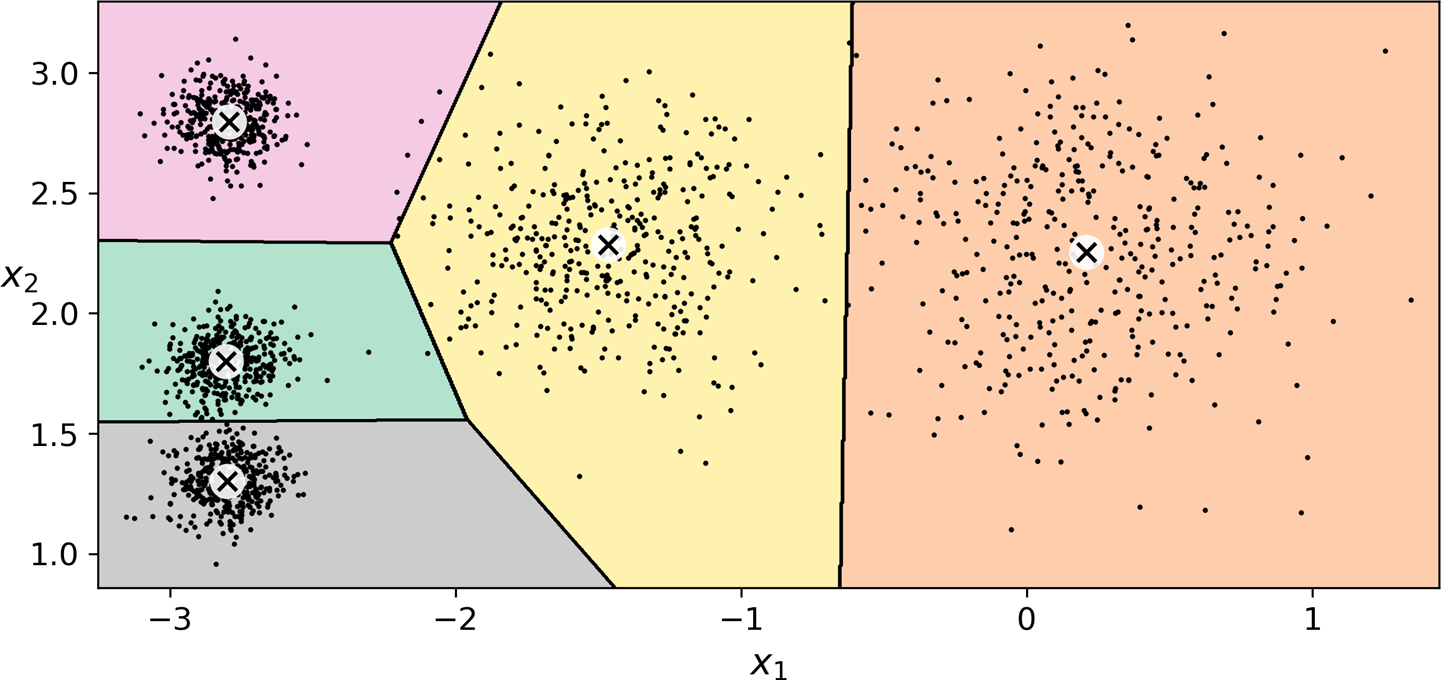
하드 군집화 대 소프트 군집화

• 하드 군집화: 각 샘플에 대해 가장 가까운 군집 선택

• 소프트 군집화: 샘플별로 각 군집 센트로이드와의 거리 측정

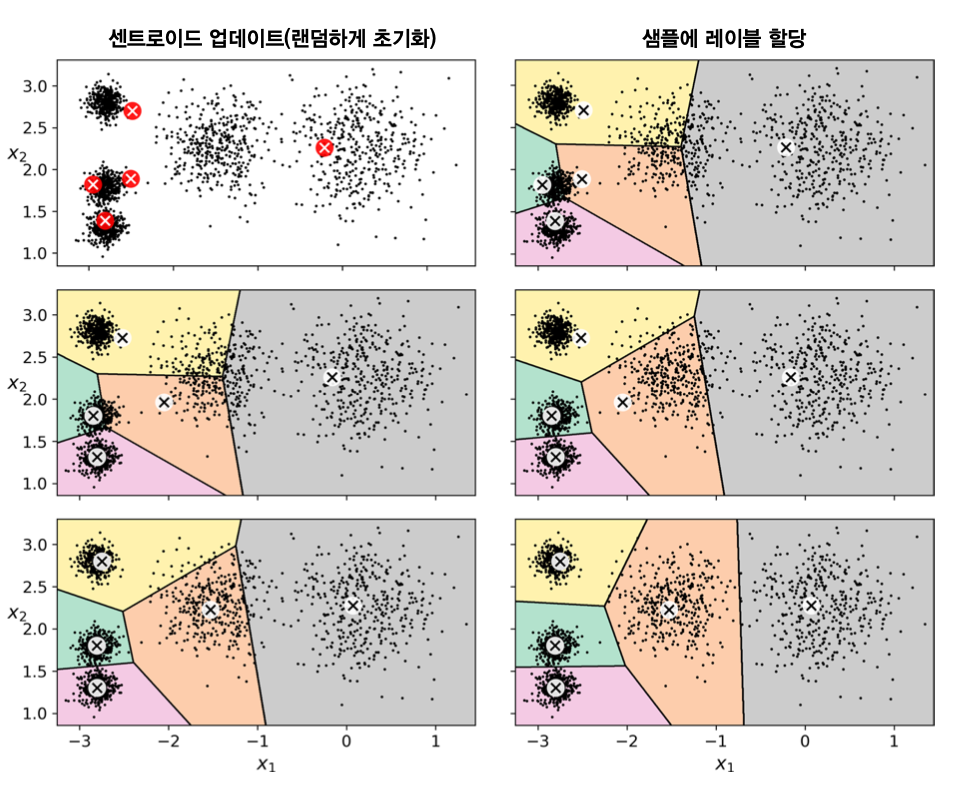
k-평균 알고리즘

• 먼저 $k$ 개의 센트로이드를 무작위로 선택한 후 수렴할 때까지 다음 과정 반복
  • 각 샘플을 가장 가까운 센트로이드에 할당
  • 군집별로 샘플의 평균을 계산하여 새로운 센트로이드 지정

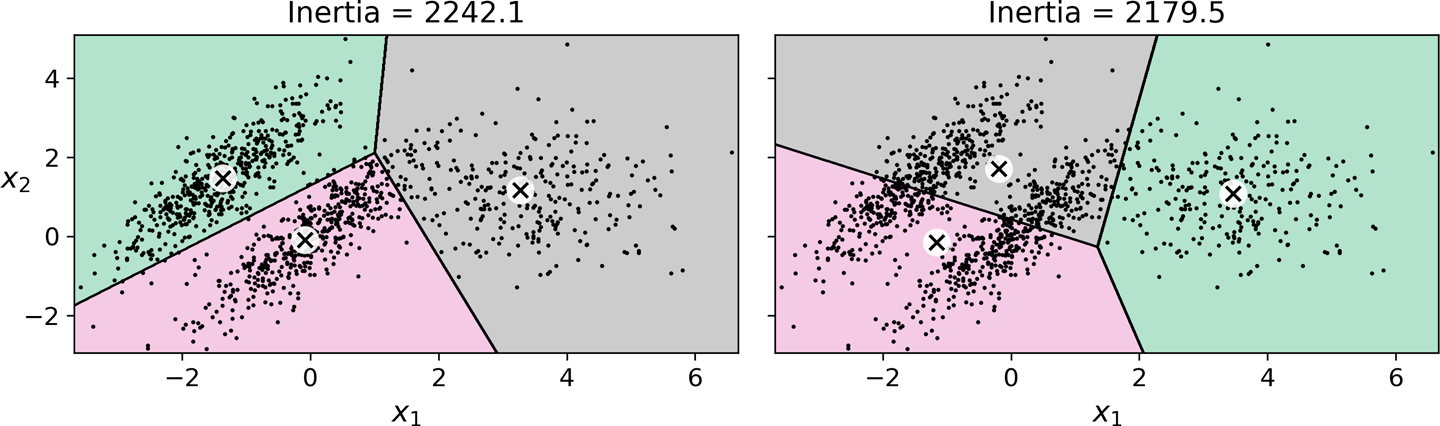
k-평균 알고리즘의 단점

• 군집의 크기가 서로 많이 다르면 잘 작동하지 않음. 이유는 샘플과 센트로이드까지의 거리만 고려되기 때문임.

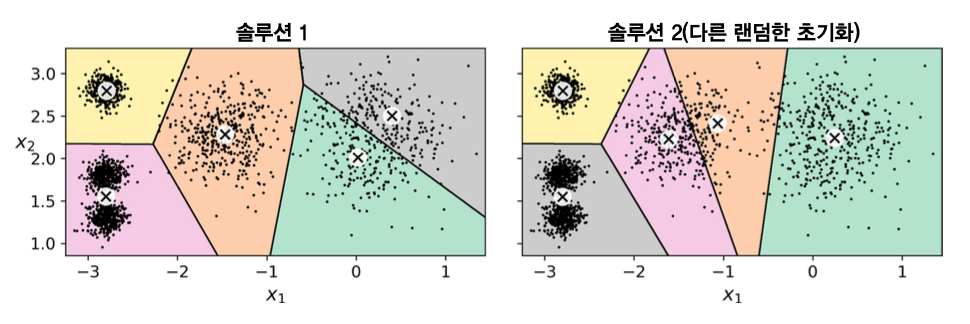
• 초기 센트로이드에 따라 매우 다른 군집화 발생 가능

관성(inertia, 이너셔)

• 샘플과 가장 가까운 센트로이드와의 거리의 제곱의 합

• 각 군집이 센트로이드에 얼마나 가까이 모여있는가를 측정

• k-평균 모델의 성능 평가 방법

• KMeans 모델의 score() 메서드가 관성의 음숫값을 계산함.
  • 점수(score)는 높을 수록 좋은 모델을 나타내도록 해야 하는데, 관성은 높을 수록 좋은 모델과 거리가 멀어지기 때문임.
  • 다양한 초기화 과정을 실험한 후에 가장 좋은 것 선택 n_init = 10이 기본값으로 사용됨. 즉, 10번 학습 후 가장 낮은 관성을 갖는 모델 선택.

KMeans 모델의 알고리즘

• k-평균++ 초기화 알고리즘

  • 센트로이드를 무작위로 초기화하는 대신 특정 확률분포를 이용하여 선택하여 센트로이드들 사이의 거리를 크게할 가능성이 높아짐.

  • 기본 아이디어: 주피터 노트북 참조

• Elkan 알고리즘

  • 각 훈련 샘플과 센트로이드 사이의 거리 계산을 획기적으로 개선한 알고리즘

미니배치 k-평균

• 미니배치를 사용해서 센트로이드를 조금씩 이동하는 k-평균 알고리즘

• 사이킷런의 MiniBatchMeans 모델이 지원.

from sklearn.cluster import MiniBatchKMeans

minibatch_kmeans = MiniBatchKMeans(n_clusters=5, random_state=42)
minibatch_kmeans.fit(X)

큰 데이터셋 다루기

• memmap 활용
  • 대용량 훈련 세트 활용하고자 할 경우
  • 8장 PCA에서 사용했던 기법과 동일

• memmap 활용이 불가능할 정도로 큰 데이터셋인 경우
  • 미니배치로 쪼개어 학습
  • MiniBatchKMeans의 partial_fit() 메서드 활용

미니배치 k-평균의 특징

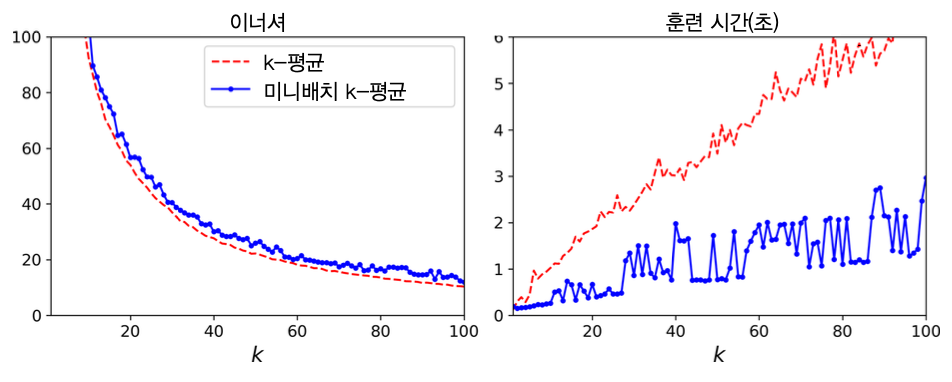
• 군집수가 커질 수록 k-평균보다 훨씬 빠르게 훈련됨. 하지만 성능 차이는 상대적으로 커짐.

• 아래 왼편 그림에서 보면 군집수 $k$가 커져도 성능 차이가 유지됨. 하지만 성능 자체가 좋아지므로 두 모델의 상대적 성능 차이는 점점 벌어짐을 의미함.

k-평균 모델의 최적의 군집수 찾기

• 군집수가 적절하지 않으면 좋지 않은 모델로 수렴할 수 있음.

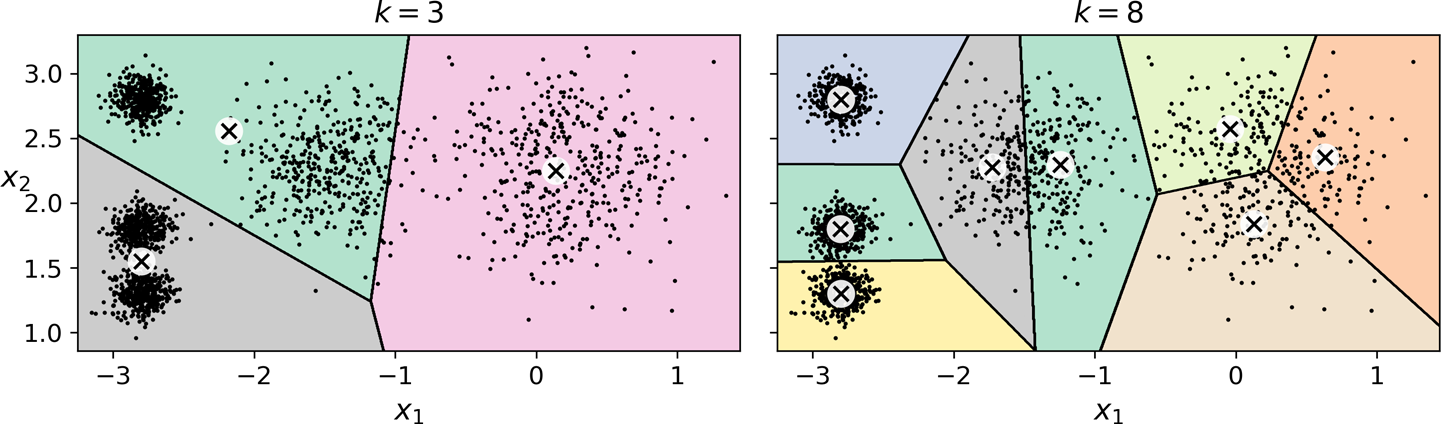
관성과 군집수

• 군집수 k가 증가할 수록 관성은 기본적으로 줄어듬. 따라서 관성만으로 모델을 평가할 없음.

• 관성이 더 이상 획기적으로 줄어들지 않는 지점을 선택할 수 있음.

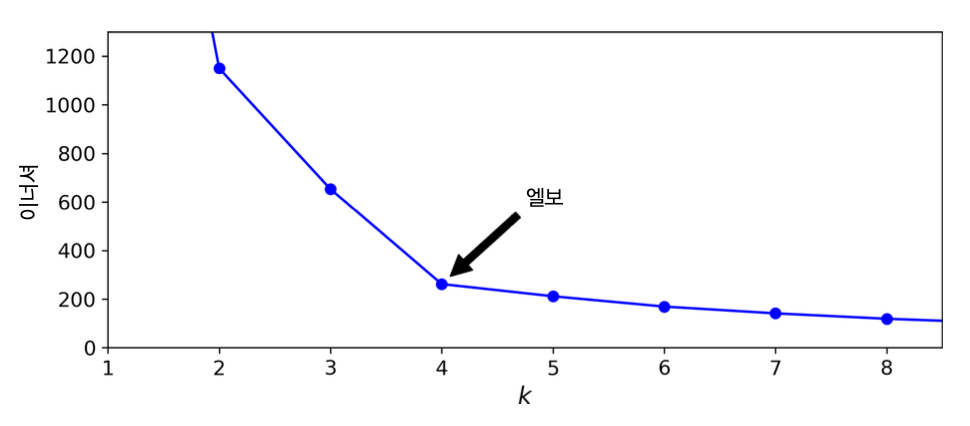
• 하지만 아래 그림에서 보듯이 반드시 좋은 모델이라 평가하기 어려움.

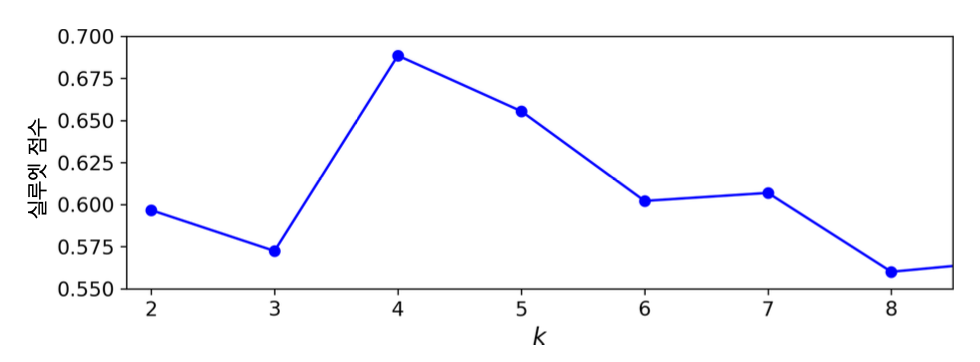
실루엣 점수와 군집수

• 샘플별 실루엣 계수

  $$\frac{b - a}{\max(a, b)}$$

  • $a$: 동일 군집 내의 다른 샘플과의 거리의 평균값
  • $b$: 가장 가까운 타 군집 샘플과의 거리의 평균값

• 실루엣 계수는 -1과 1사이의 값임.
  • 1에 가까운 값: 적절한 군집에 포함됨.
  • 0에 가까운 값: 군집 경계에 위치
  • -1에 가까운 값: 잘못된 군집에 포함됨

• 실루엣 점수: 실루엣 계수의 평균값.

• 실루엣 점수가 높은 모델을 선택할 수 있음. 아래 그림에 의해 k=5도 좋은 선택이 될 수 있지만 확실하지는 않음.

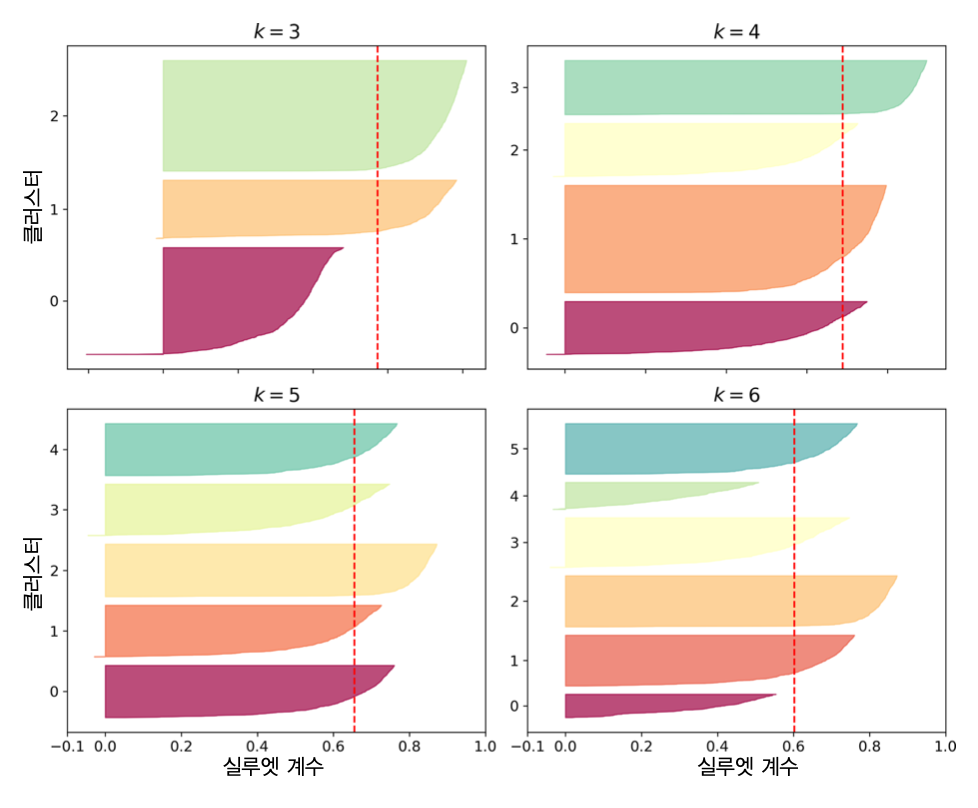
실루엣 다이어그램과 군집수

• 실루엣 다이어그램: 군집별 실루엣 계수들의 모음. 군집별로 칼날 모양 형성.

  • 칼날 두께: 군집에 포함된 샘플 수
  • 칼날 길이: 군집에 포함된 각 샘플의 실루엣 계수

• 빨간 파선: 군집별 실루엣 점수. 대부분의 칼날이 빨간 파선보다 길어야 함.

• 칼날의 두께가 서로 비슷해야, 즉, 군집별 크기가 비슷해야 좋은 모델임. 따라서 k=5 가 보다 좋은 모델임.

k-평균의 한계

• 최적의 모델을 구하기 위해 여러 번 학습해야 함.
• 군집수를 미리 지정해야 함.
• 군집의 크기나 밀집도가 다르거나, 원형이 아닐 경우 잘 작동하지 않음.

군집화 활용

이미지 색상 분할

• 동일한 종류의 물체는 동일한 영역에 할당됨. 예를 들어, 보행자들을 모두 하나의 영역, 또는 각각의 영역으로 할당 가능.

• 합성곱 신경망이 가장 좋은 성능 발휘

• 색상 분할: 유사 색상으로 이루어진 군집으로 분할.

• 예제: 무당벌레 이미지 색상 분할

차원축소

• transform() 메서드
  • 데이터 샘플에 대해 각 센트로이드부터의 거리로 이루어진 어레이 생성.
  • n 차원의 데이터셋을 k 차원의 데이터셋으로 변환함.

• 예제: 미니 MNIST 데이터셋 전처리. $k=50$.

pipeline = Pipeline([
    ("kmeans", KMeans(n_clusters=50, random_state=42)),
    ("log_reg", LogisticRegression(multi_class="ovr", solver="lbfgs", max_iter=5000)),
    ])
pipeline.fit(X_train, y_train)

• 전처리 단계로 k-평균을 활용하기에 그리드 탐색 등을 이용하여 최적의 군집수 확인 가능.
  • 최적 군집수: 99
  • 모델 정확도: 98.22%

준지도 학습

• 레이블이 있는 데이터가 적고, 레이블이 없는 데이터가 많을 때 활용

• 예제: 미니 MNist (계속)
  • 예를 들어, 50개의 군집으로 나눈 후 50개 군집별로 센트로이드에 가장 가까운 샘플을 대표 이미지로 선정.
  • 선정된 50개 샘플만을 이용하여 훈련해도 92.22%의 정확도가 달성됨.

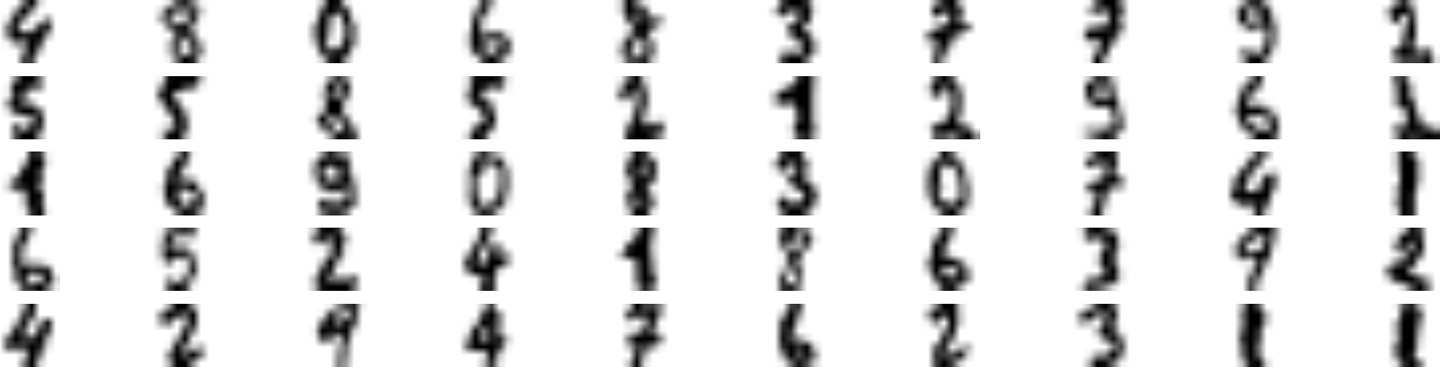
레이블 전파

• 대표이미지의 레이블을 해당 군집의 모든 샘플로 전파 가능. 하지만 전파된 레이블의 정확도가 낮을 수 있음.

• 센트로이드에 가까운 20% 정도에게만 레이블 전파하는 것 추천. 이유는 센트로이드에 가깝기 떼문에 레이블의 정확도가 매우 높음. 이런 방식으로 보다 적은 크기의 데이터셋으로 효율적인 모델 훈련이 가능해짐.

준지도학습과 능동학습

• 분류기 모델이 가장 불확실하기 예측하는 샘플에 레이블 추가하기

• 가능하면 서로 다른 군집에서 선택.

• 새 모델 학습

• 위 과정을 성능향상이 약해질 때까지 반복.

DBSCAN

• 연속적인 밀집 지역을 하나의 군집으로 설정.

사이킷런의 DBSCAN 모델

• 두 개의 하이퍼파라미터 사용
  • eps: $\varepsilon$-이웃 범위
    • 주어진 기준값 $\varepsilon$ 반경 내에 위치한 샘플
  • min_samples: $\varepsilon$ 반경 내에 위치하는 이웃의 수

핵심샘플과 군집

• 핵심샘플: $\varepsilon$ 반경 내에 자신을 포함해서 min-samples개의 이웃을 갖는 샘플

• 군집: 핵심샘플로 이루어진 이웃들로 구성된 그룹

이상치

• 핵심샘플이 아니면서 동시에 핵심샘플의 이웃도 아닌 샘플.

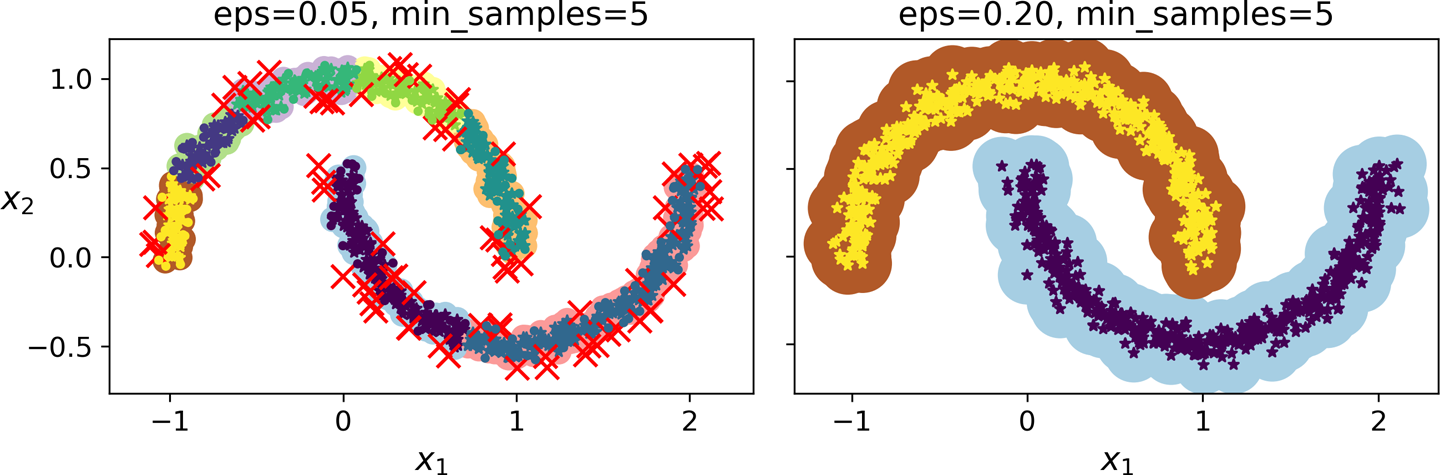
예제

• 반달모양 데이터 활용

---

from sklearn.cluster import DBSCAN

dbscan = DBSCAN(eps=0.05, min_samples=5)
dbscan.fit(X)

---

DBSCAN과 예측

• predict() 메서드 지원하지 않음.

• 이유: KNeighborsClassifier 등 보다 좋은 성능의 분류 알고리즘 활용 가능.

• 아래 코드: 핵심샘플 대상 훈련.

---

from sklearn.neighbors import KNeighborsClassifier

knn = KNeighborsClassifier(n_neighbors=50)
knn.fit(dbscan.components_, dbscan.labels_[dbscan.core_sample_indices_])

---

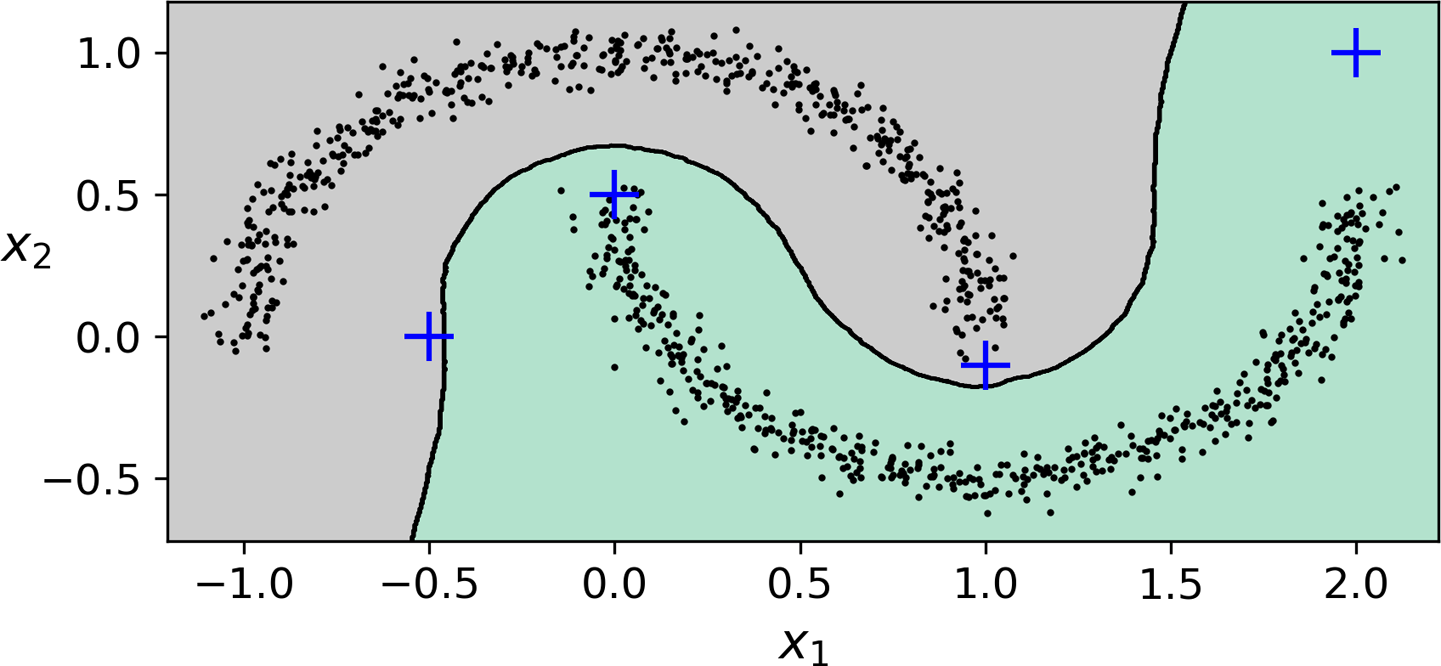
• 이후 새로운 샘플에 대한 예측 가능
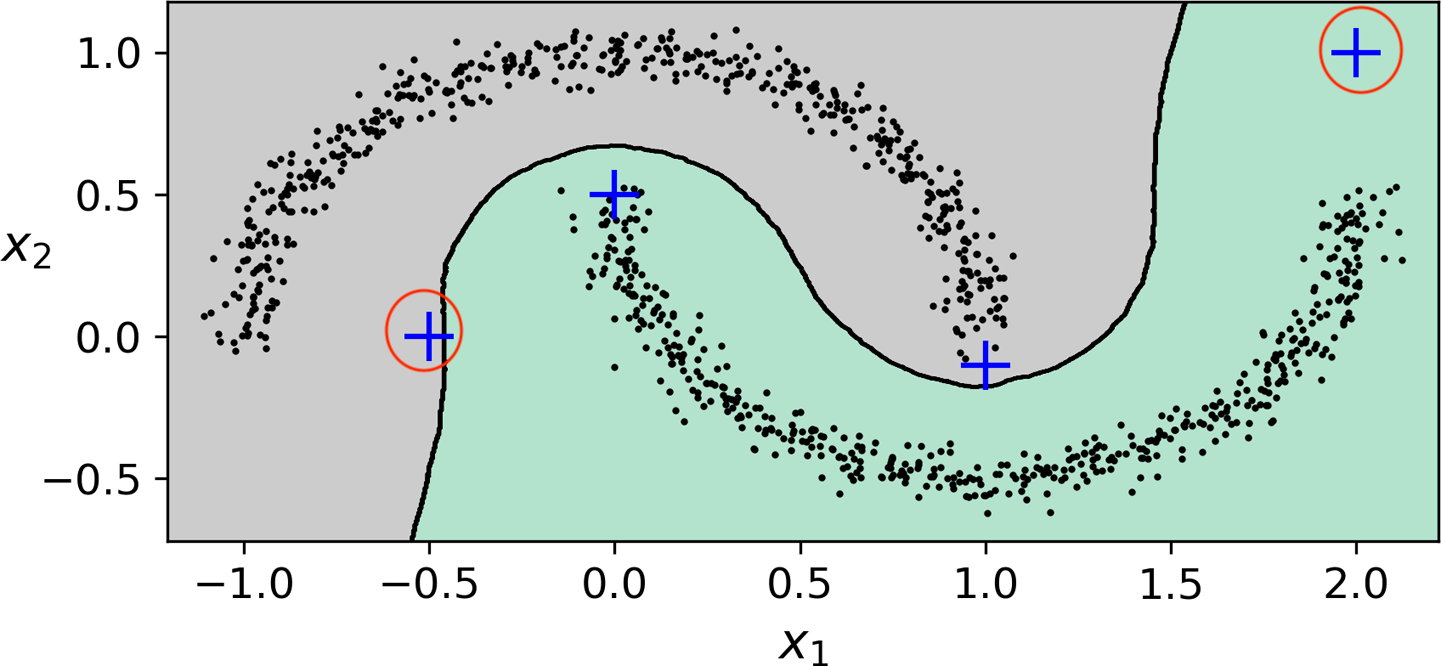
• 아래 그림은 새로운 4개의 샘플에 대한 예측을 보여줌.

이상치 판단

• 위 예제에서, 두 군집으로부터 일정거리 이상 떨어진 샘플을 이상치로 간주 가능.

• 예를 들어, 양편 끝쪽에 위치한 두 개의 샘플이 이상치로 간주될 수 있음.

DBSCAN의 장단점

• 매우 간단하면서 매우 강력한 알고리즘.
  • 하이퍼파라미터: 단 2개

• 군집의 모양과 개수에 상관없음.

• 이상치에 안정적임.

• 군깁 간의 밀집도가 크게 다르면 모든 군집 파악 불가능.

계산복잡도

• 시간복잡도: 약 $O(m\, \log m)$. 단, $m$은 샘플 수

• 공간복잡도: 사이킷런의 DBSCAN 모델은 $O(m^2)$의 메모리 요구.
  • eps가 커질 경우.

기타 군집 알고리즘

• 응집 군집(병합 군집, agglomerative clustering)
• BIRCH
• 평균-이동
• 유사도 전파
• 스펙트럼 군집

9.2 가우시안 혼합 모델

• 데이터셋이 여러 개의 혼합된 가우시안 분포를 따르는 샘플들로 구성되었다고 가정.

• 가우시안 분포 = 정규분포

정규분포 소개

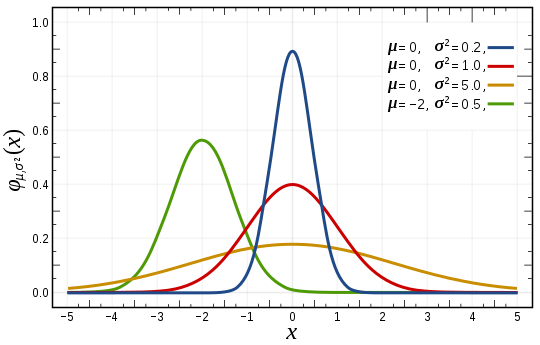
• 종 모양의 확률밀도함수를 갖는 확률분포

군집

• 하나의 가우시안 분포에서 생생된 모든 샘플들의 그룹
• 일반적으로 타원형 모양.

예제

• 아래 그림에서처럼 일반적으로 모양, 크기, 밀집도, 방향이 다름.
• 따라서 각 샘플이 어떤 정규분포를 따르는지를 파악하는 게 핵심.

GMM 활용

• 위 데이터셋에 GaussianMixture 모델 적용

• n_components: 군집수 지정

• n_init: 모델 학습 반복 횟수.
  • 파라미터(평균값, 공분산 등)를 무작위로 추정한 후 수렴할 때까지 학습시킴.

---

from sklearn.mixture import GaussianMixture

gm = GaussianMixture(n_components=3, n_init=10, random_state=42)
gm.fit(X)

---

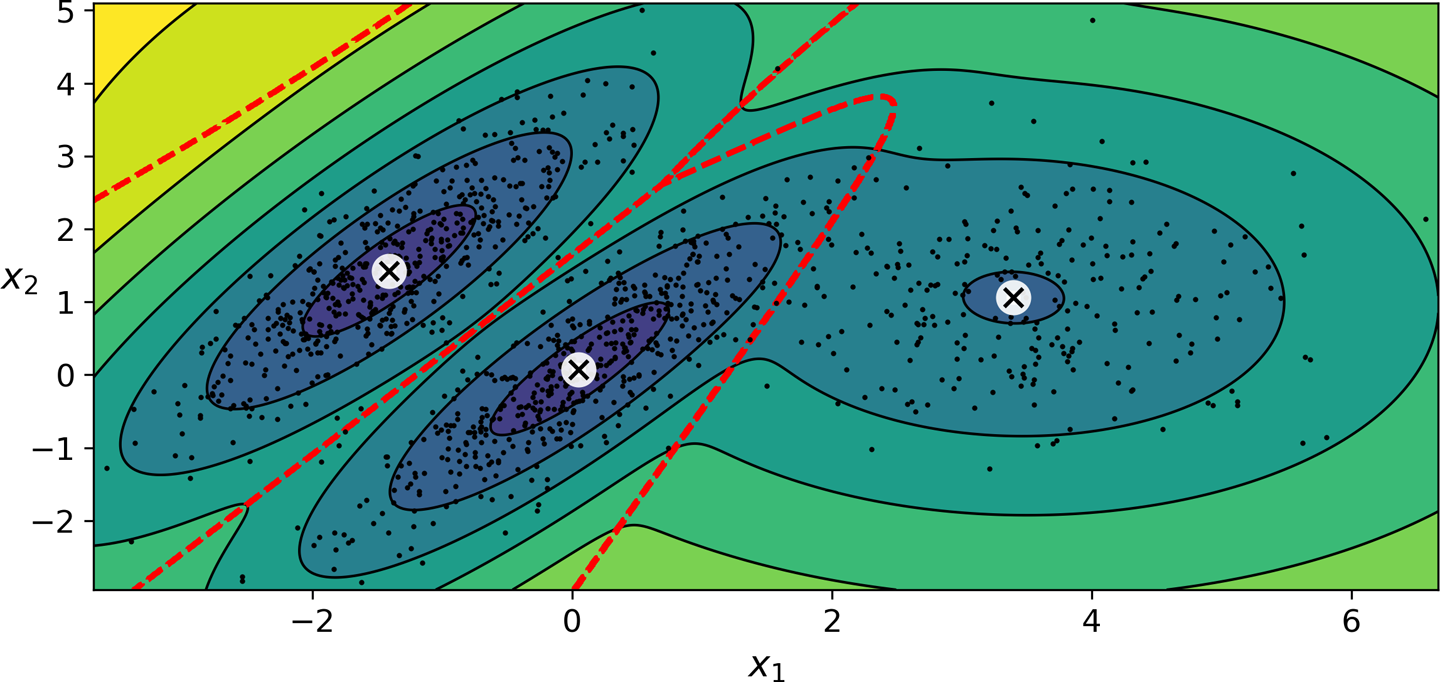
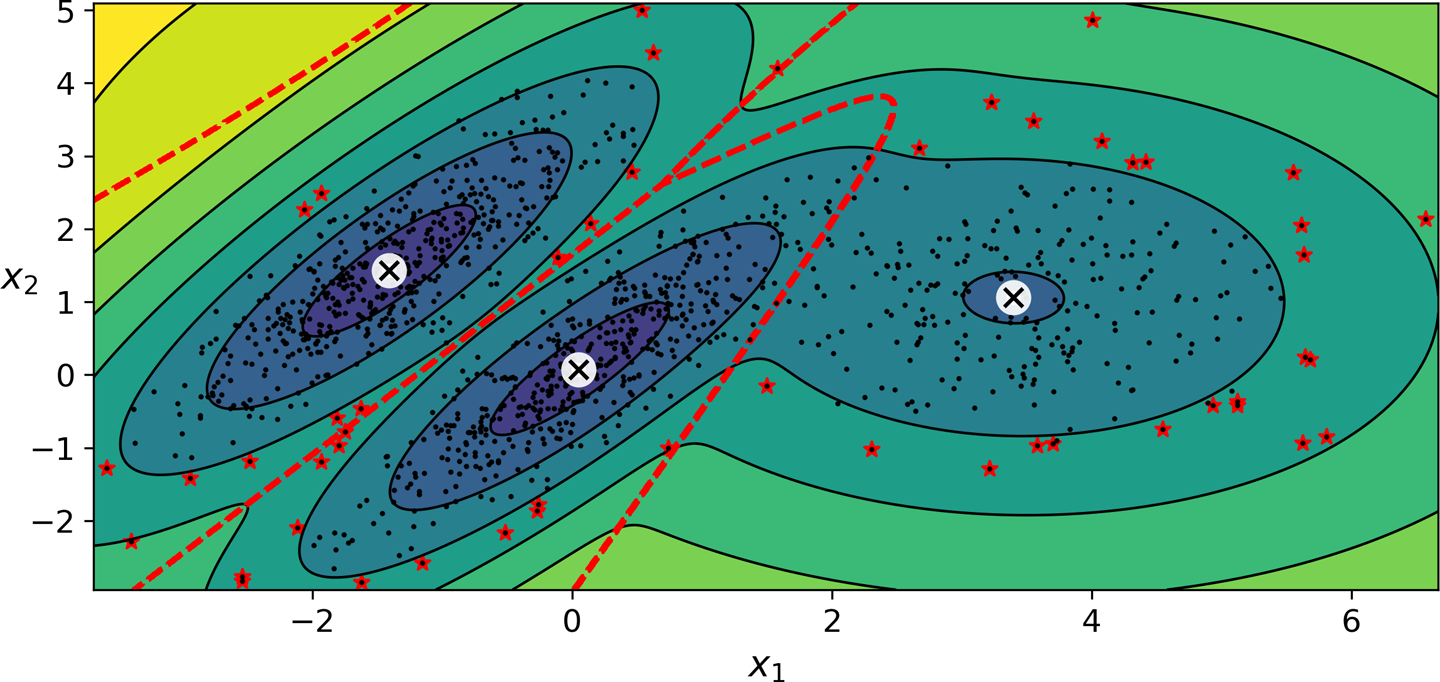
• 아래 그림은 학습된 모델을 보여줌.
  • 군집 평균, 결정 경계, 밀도 등고선

GMM 모델 규제

• 특성수가 크거나, 군집수가 많거나, 샘플이 적은 경우 최적 모델 학습 어려움.
• 공분산(covariance)에 규제를 가해서 학습을 도와줄 수 있음.
  • covariance_type 설정.

covariance_type 옵션값

• full
  • 아무런 제한 없음.
  • 기본값임.

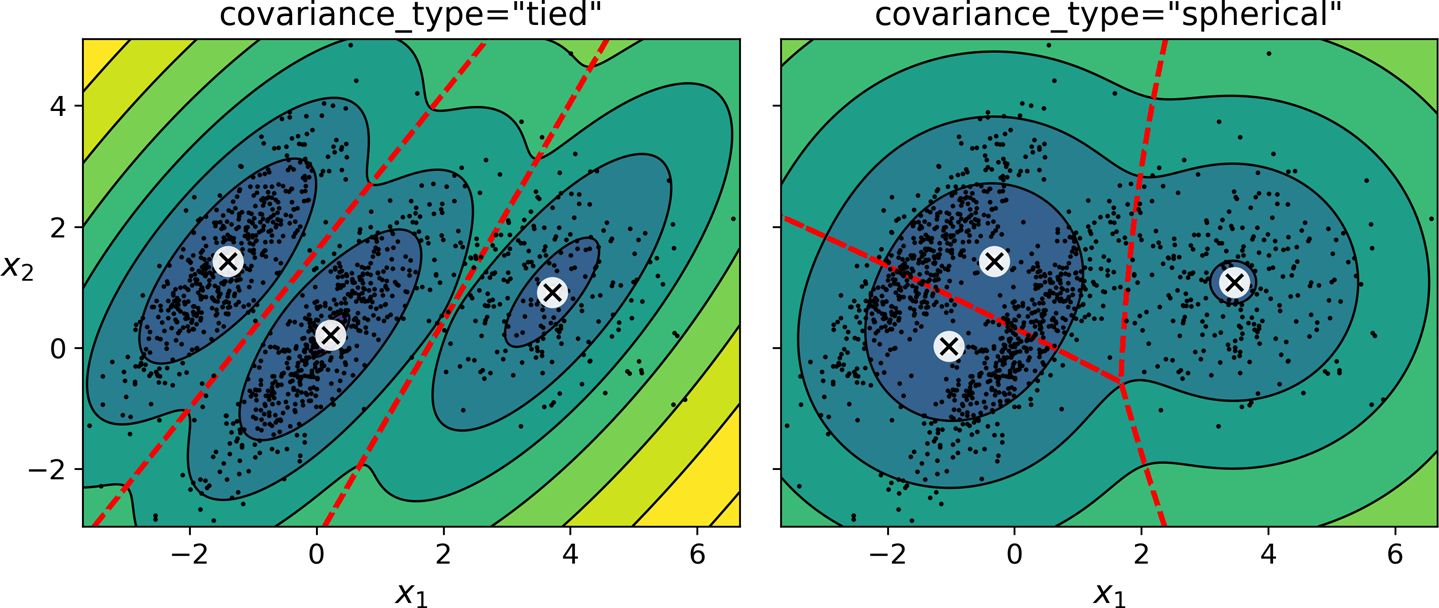
• spherical
  • 군집이 원형이라 가정.
  • 지름(분산)은 다를 수 있음.

• diag
  • 어떤 타원형도 가능.
  • 단. 타원의 축이 좌표축과 평행하다고 가정.

• tied
  • 모든 군집의 동일 모양, 동일 크기, 동일 방향을 갖는다고 가정.

가우시안 혼합 모델 활용: 이상치 탐지

• 밀도가 임곗값보다 낮은 지역에 있는 샘플을 이상치로 간주 가능.

가우션 혼합모델 군집수 지정

• k-평균에서 사용했던 관성 또는 실루엣 점수 사용 불가.
  • 군집이 타원형일 때 값이 일정하지 않기 때문.

• 대신에 이론적 정보 기준 을 최소화 하는 모델 선택 가능.

이론적 정보 기준

• BIC: Bayesian information criterion

  $$ \log(m)\, p - 2 \log (\hat L)$$

• AIC: Akaike information criterion

  $$ 2\, p - 2 \log (\hat L)$$

• $m$: 샘플 수
• $p$: 모델이 학습해야 할 파라미터 수
• $\hat L$: 모델의 가능도 함수의 최댓값

• 학습해야 할 파라미터가 많을 수록 벌칙이 가해짐.
• 데이터에 잘 학습하는 모델일 수록 보상을 더해줌.

군집수와 정보조건

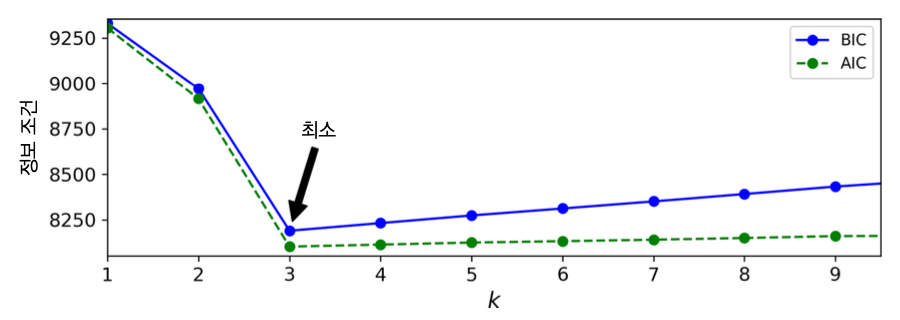
• 아래 그림은 군집수 $k$와 AIC, BIC의 관계를 보여줌.
• $k=3$이 최적으로 보임.

베이즈 가우시안 혼합 모델

• 베이즈 확률통계론 활용

BayesianGaussianMixture 모델

• 최적의 군집수를 자동으로 찾아줌.
• 단, 최적의 군집수보다 큰 수를 n_components에 전달해야 함.
  • 즉, 군집에 대한 최소한의 정보를 알고 있다고 가정.
• 자동으로 불필요한 군집 제거

---

from sklearn.mixture import BayesianGaussianMixture

bgm = BayesianGaussianMixture(n_components=10, n_init=10, random_state=42)
bgm.fit(X)

---

• 결과는 군집수 3개를 사용한 이전 결과와 거의 동일.
• 군집수 확인 가능

>>> np.round(bgm.weights_, 2)
array([0.4 , 0.21, 0.4 , 0.  , 0.  , 0.  , 0.  , 0.  , 0.  , 0.  ])

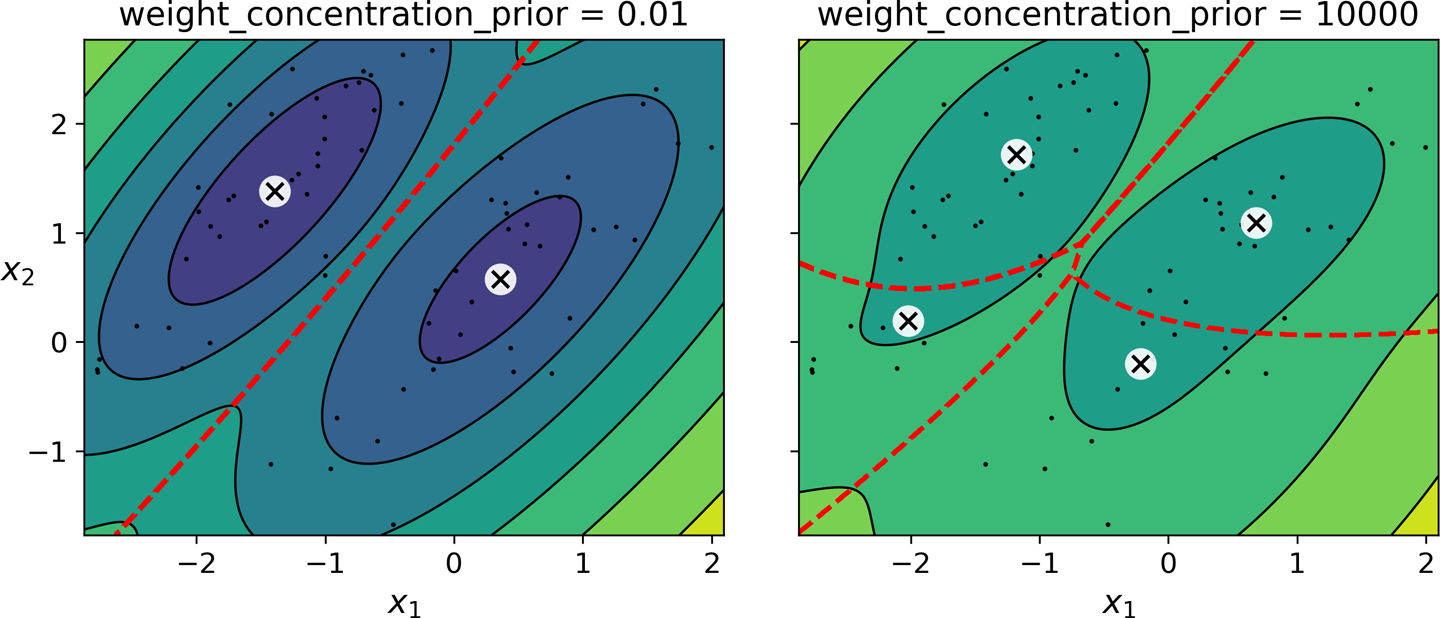
사전 믿음

• 군집수가 어느 정도일까를 나타내는 지수
• weight_concentration_prior 하이퍼파라미터
  • n_components에 설정된 군집수에 대한 규제로 사용됨.
  • 작은 값이면 특정 군집의 가중치를 0에 가깝게 만들어 군집수를 줄이도록 함.
  • 즉, 큰 값일 수록 n_components에 설정된 군집수가 유지되도록 함.

가우시안 혼합 모델의 장단점

• 타원형 군집에 잘 작동.

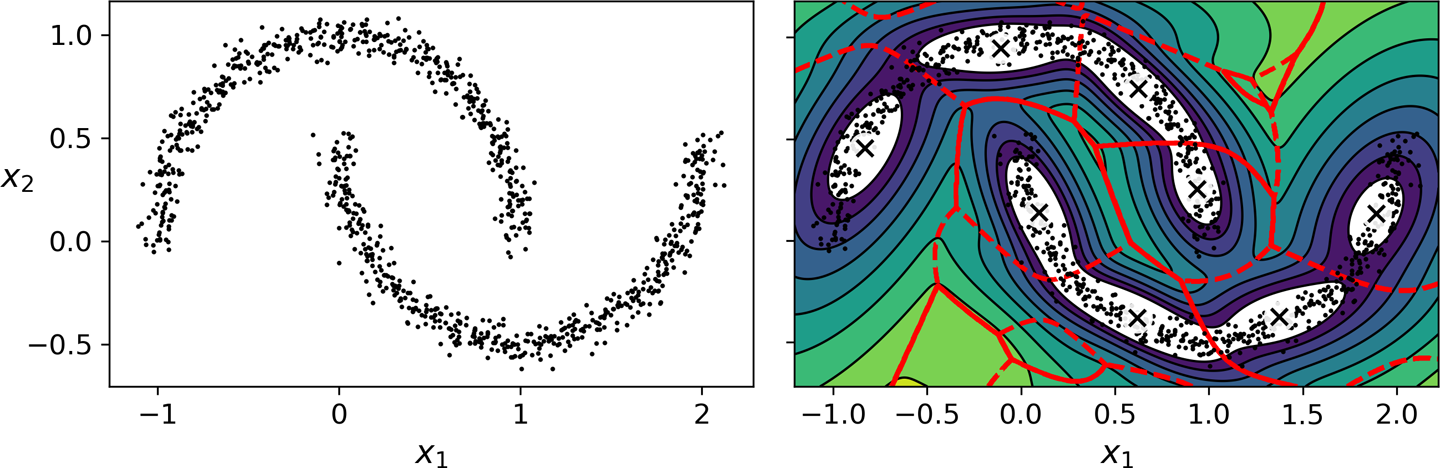
• 하지만 다른 모양을 가진 데이터셋에서는 성능 좋지 않음.

• 예제: 달모양 데이터에 적용하는 경우
  • 억지로 타원을 찾으려 시도함.

이상치 탐지와 특이치 탐지를 위한 다른 알고리즘

• PCA
• Fast-MCD
• 아이솔레이션 포레스트
• LOF
• one-class SVM