8장 차원축소¶
감사의 글¶
자료를 공개한 저자 오렐리앙 제롱과 강의자료를 지원한 한빛아카데미에게 진심어린 감사를 전합니다.
주요 내용¶
- 차원의 저주
- 차원축소를 위한 접근법
- 사영
- 다양체 학습
- 사영 기법 알고리즘
- PCA(주성분 분석)
- 커널 PCA
- 다양체 학습 알고리즘
- LLE(국소적 선형 임베딩)
기본 아이디어¶
- 차원의 저주: 샘플의 특성이 너무 많으면 학습이 매우 어려워짐.
- 차원축소: 특성 수를 (크게) 줄여서 학습 불가능한 문제를 학습 가능한 문제로 만드는 기법
- 차원축소로 인한 정보손실을 어느 정도 감안하면서 훈련 속도와 성능을 최대로 유지하는 것이 목표
활용 예제¶
- MNIST 데이터셋
- 사진의 중앙에만 집중해도 숫자 인식에 별 문제 없음.
- 주성분 분석(PCA) 기법을 이용하여 784개 픽셀 대신 154개만 대상으로 충분히 학습 가능
- 데이터 시각화
- 차원을 2, 3차원으로 줄이면 그래프 시각화 가능
- 군집 같은 시각적인 패턴을 감지하여 데이터에 대한 통찰 얻을 수 있음.
8.1 차원의 저주¶
고차원 공간¶
- 3차원을 초과하는 고차원의 공간을 상상하기 매우 어려움.
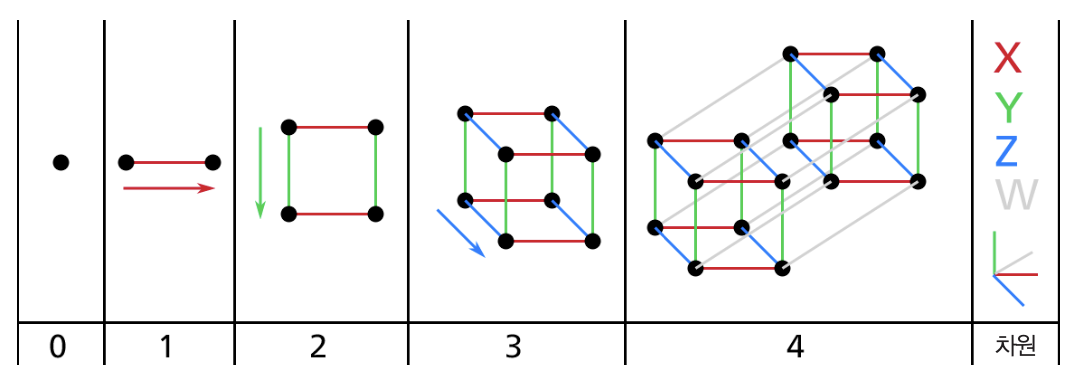
차원의 저주¶
- 차원의 커질 수록 두 지점 사이의 거리가 매우 커짐.
- 즉, 특성 수가 아주 많은 경우, 훈련 샘플 사이의 거리가 매우 커서 과대적합 위험도가 커짐.
- 이유: 두 샘플 사이의 거리가 멀어서 기존 값들을 이용한 추정(예측)이 여러 과정을 거쳐야 하기 때문임.
- 해결책: 샘플 수 늘리기. 하지만 고차원의 경우 충분히 많은 샘플 수를 준비하는 일은 사실상 불가능.
8.2 차원축소 기법¶
기본 아이디어¶
- 모든 훈련 샘플이 고차원 공간의 일부인 저차원 부분공간에 가깝게 놓여 있는 경우가 일반적으로 발생
- 예제: 아래 두 이미지 모두 3차원(3D) 공간상의 데이터셋을 보여줌. 하지만 데이터셋 자체는 2차원 형식을 따름.
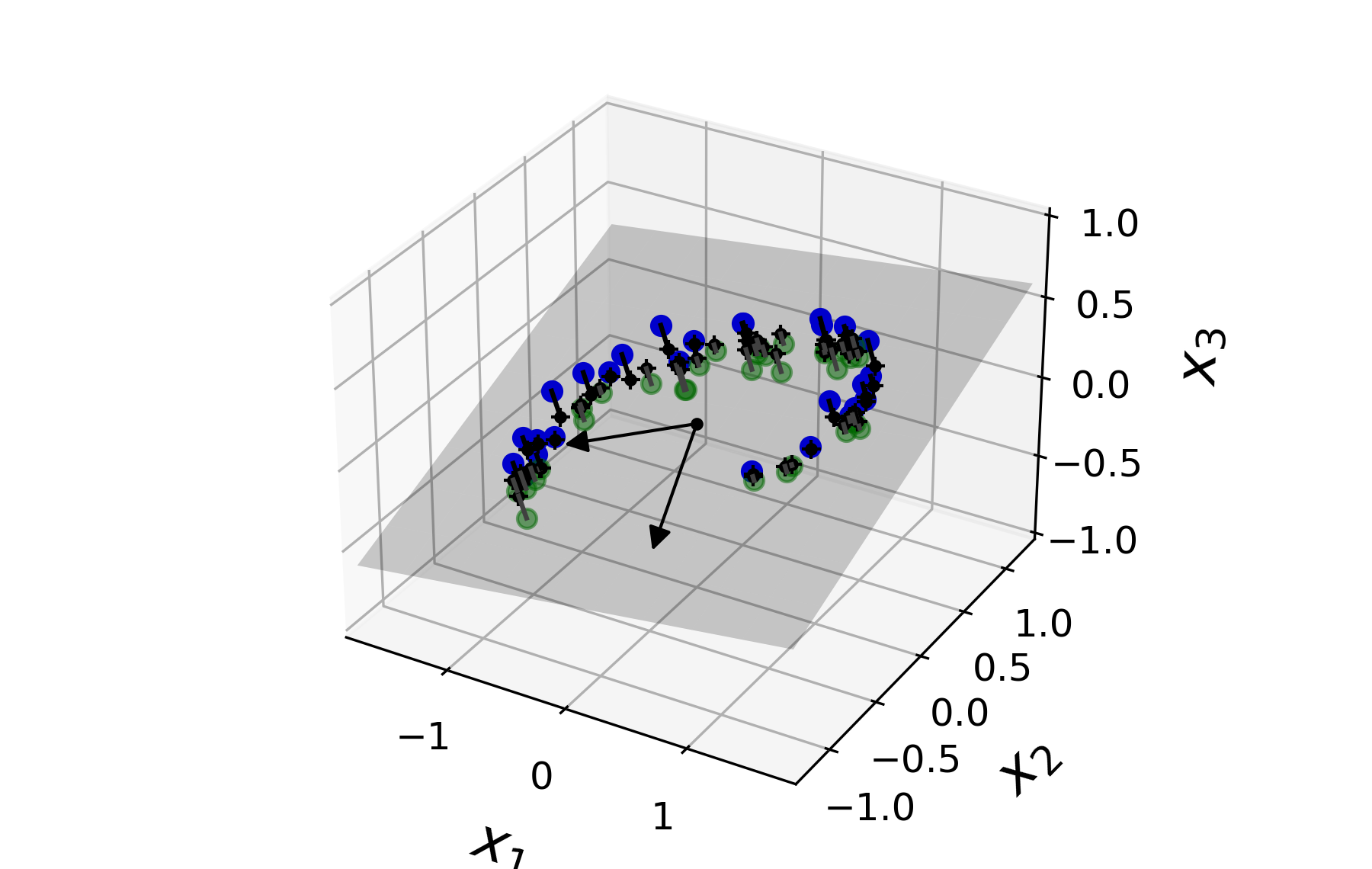 |
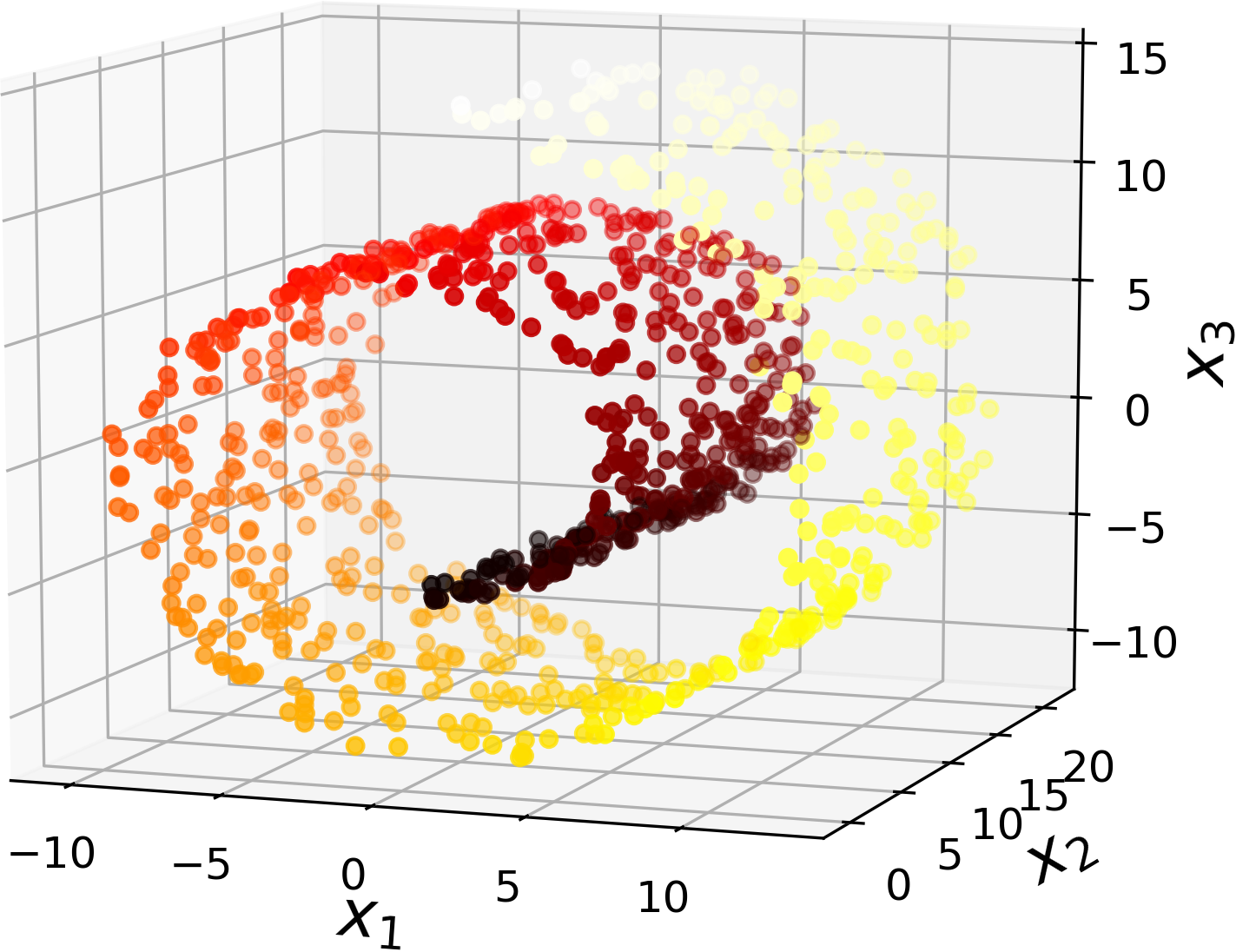 |
대표적인 차원축소 기법¶
- 사영(projection)
- 다양체 학습(manifold learning)
사영 기법¶
- $n$차원 공간에 존재하는 $d$차원 부분공간을 $d$차원 공간으로 사영하기. 단, $d < n$.
- 예제
- 왼쪽 3차원에 존재하는 적절한 2차원 평면으로 사영하면 적절한 2차원 상의 이미지를 얻게됨.
- 오른쪽 2차원 이미지에 사용된 축 $z_1$과 $z_2$를 적절하게 찾는 게 주요 과제임.
 |
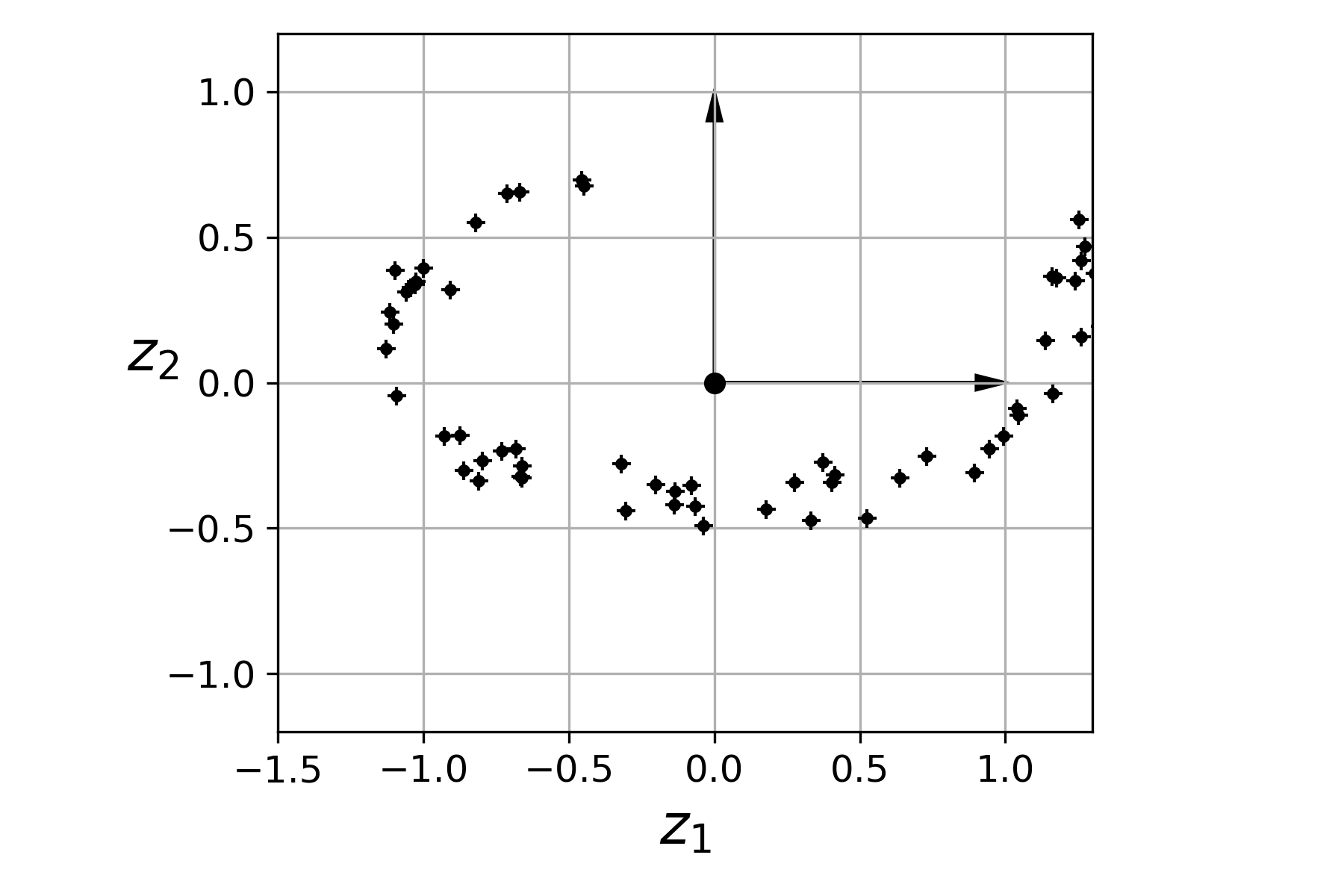 |
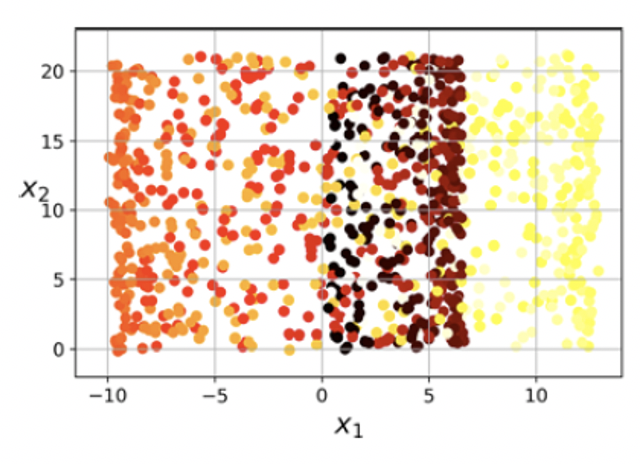
부적절한 사영¶
- 사영이 경우에 따라 보다 복잡한 결과를 낼 수 있음.
- 롤케이크를 $x_1$과 $x_2$ 축으로 사영하면 샘플 구분이 보다 어려워짐.
 |
 |
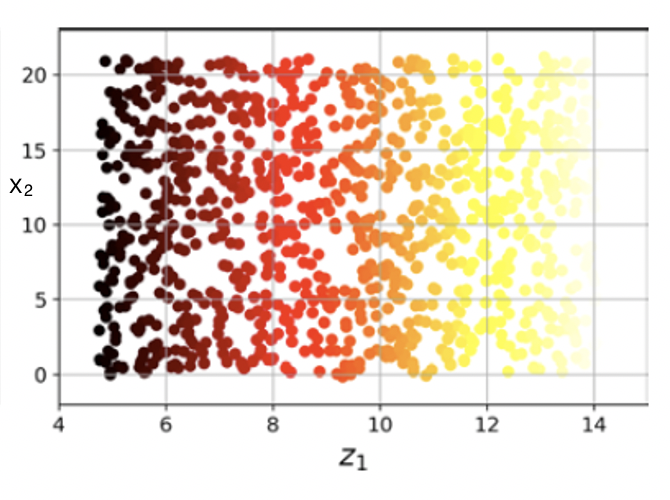
다양체 학습¶
- 롤케이크의 경우 사영 보다는 돌돌 말린 것을 펼치면 보다 적절한 2차원 이미지를 얻게 됨.
 |
 |
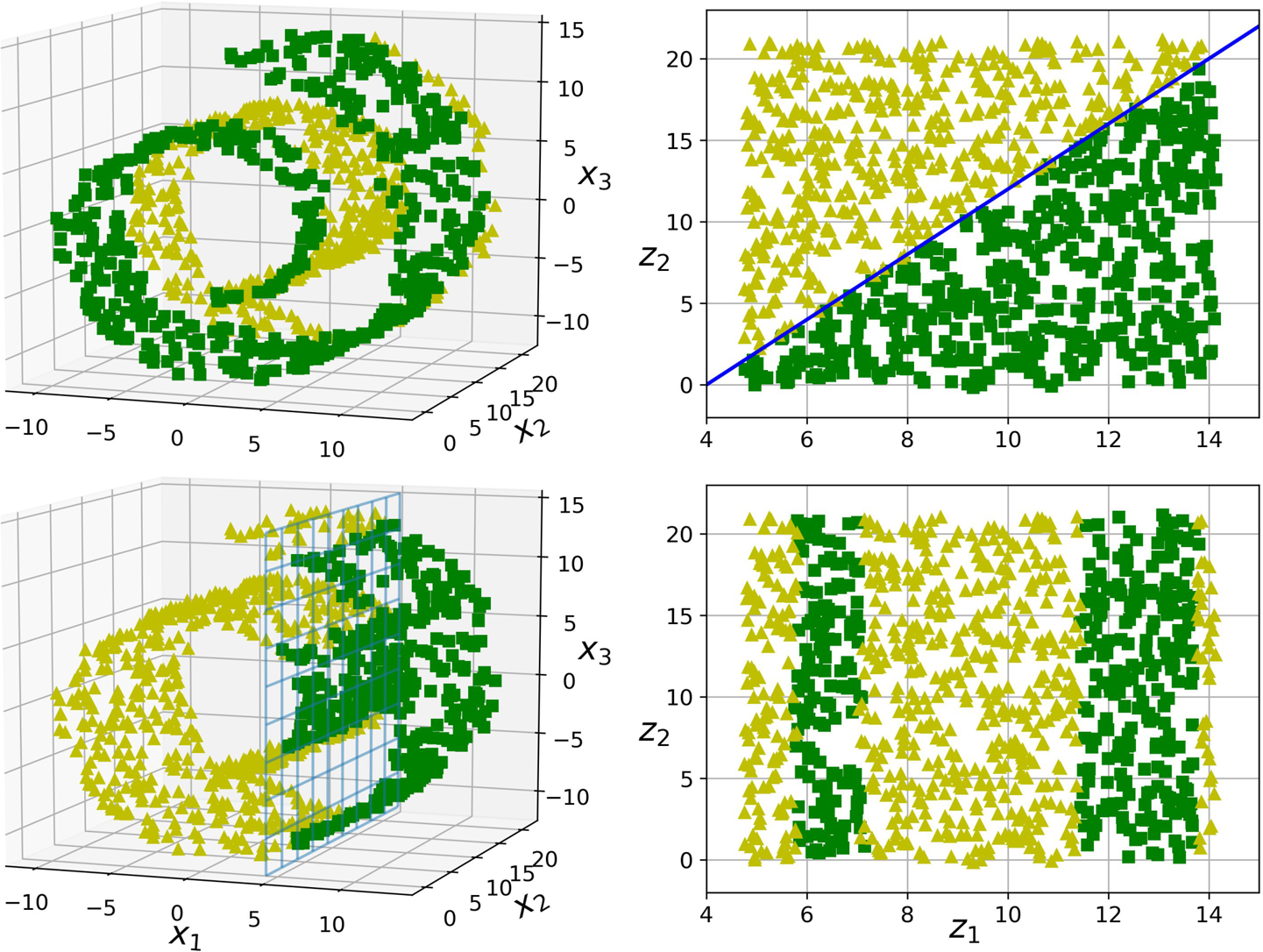
다양체 가정¶
대부분의 고차원 데이터셋이 더 낮은 차원의 다양체게 가깝다는 가정
저차원의 다양체 공간으로 차원축소를 진행하면 보다 간단한 다양체가 된다라는 가정과 함께 사용되지만 일반적으로 사실 아님. (아래 그림 참조)
차원축소 알고리즘¶
- 사영
- PCA(주성분 분석): 선형 PCA, 랜덤 PCA, 점진적 PCA
- 커널 PCA (비선형 사영): 선형 커널, RBF 커널, 시그모이드 커널
- 기타: 랜덤 사영(Random Projection), LDA(선형 판별 분석, Linear Discriminant Analysis)
- 다양체 학습
- LLE(지역 선형 임베딩)
- 기타: MDS, Isomap, t-SNE 등
8.3 PCA¶
아이디어¶
- 훈련 데이터에 가장 가까운 초평면(hyperplane)을 정의한 다음, 그 평면에 사영하는 기법
- 주성분 분석(PCA, Principal Component Analysis)이 핵심.
- 분산 보존 개념과 주성분 개념이 중요함.
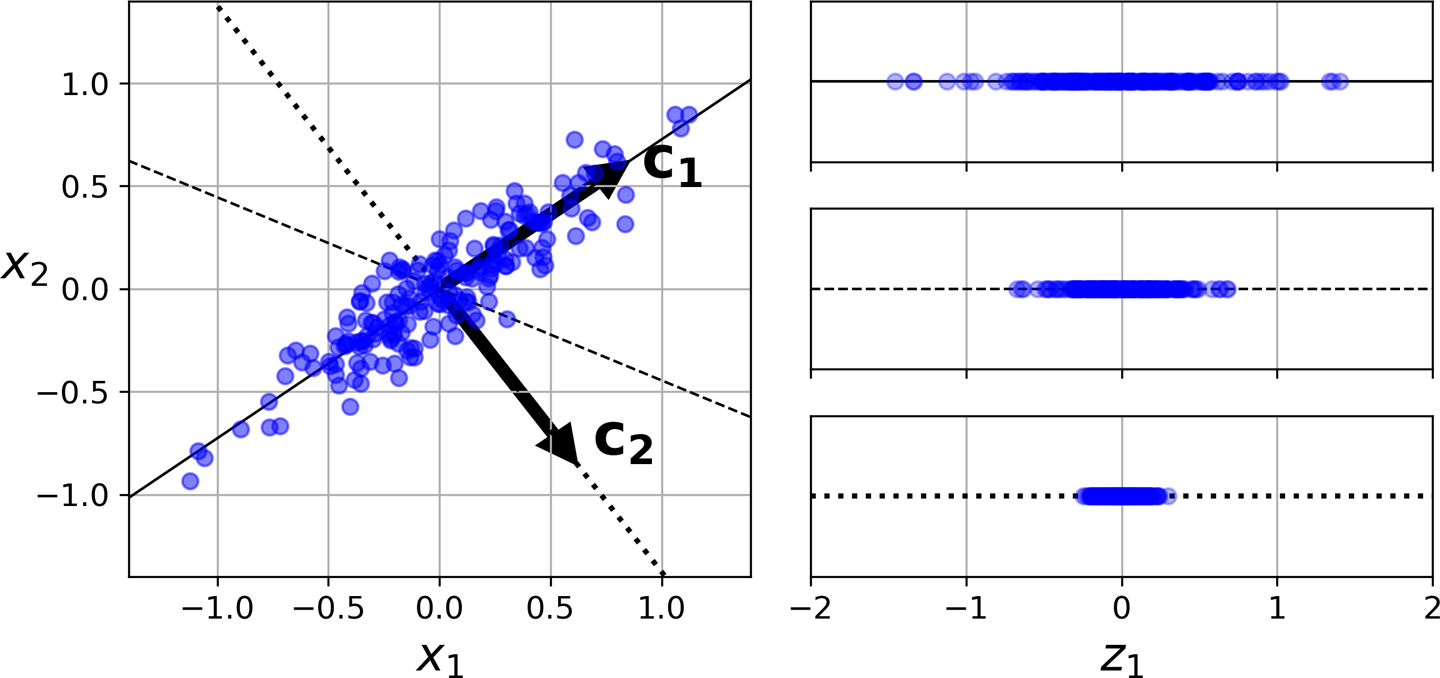
분산 보존¶
- 분산 보존: 저차원으로 사영할 때 훈련 세트의 분산이 최대한 유지되도록 축을 지정해야 함.
- 예제: 아래 그림에서 $c_1$ 벡터가 위치한 실선 축으로 사영하는 경우가 분산을 최대한 보존함. 그러면 $c_1$에 수직이면서 분산을 최대로 보존하는 축은 $c_2$임.
주성분¶
- 첫째 주성분: 분산을 최대한 보존하는 축
- 둘째 주성분: 첫째 주성분과 수직을 이루면서 분산을 최대한 보존하는 축
- 셋째 주성분: 첫째, 둘째 주성분과 수직을 이루면서 분산을 최대한 보존하는 축
- ...
주성분과 사영¶
- 특잇값 분해(SVD) 기법을 이용하면 쉽게 해결됨.
특잇값 분해: m x n 모양을 가지며, 평균값이 0인 데이터셋 $X$가 주어졌을 때 아래 조건을 만족시키는 세 개의 행렬 $U$, $\Sigma$, $V$가 존재.
- $U$: m x m 행렬
- $\Sigma$: m x n 모양의 대각행렬(diagonal matrix).
$V$: n x n 행렬. 윗첨자 $T$는 전치행렬을 의미함.
$$ X = U\, \Sigma \, V^{\!T} $$
주성분 벡터는 행렬 $V$의 열에 해당하며, 따라서 $d$차원으로의 사영은 아래와 같이 계산됨:
$$ X\, (V\text{[: , :d]}) $$
사이킷런 사용하기¶
- 사이킷런의 PCA 모델 제공
- SVD 기법 활용
예제: 데이터셋의 차원을 2로 줄이기
from sklearn.decomposition import PCA pca = PCA(n_components = 2) X2D = pca.fit_transform(X)
설명 분산 비율¶
explained_variance_ration_속성 변수: 각 주성분에 대한 원 데이터셋의 분산 비율 저장
- 예제: 아래 사영 그림에서 설명된 3차원 데이터셋의 경우.
- $z_1$ 축: 84.2%
- $z_2$ 축: 14.6%
 |
 |
적절한 차원¶
- 적절한 차원: 밝혀진 분산 비율의 합이 95% 정도 되도록 하는 주성분들로 구성
- 데이터 시각화 목적의 경우: 2개 또는 3개
설명 분산 비율 활용¶
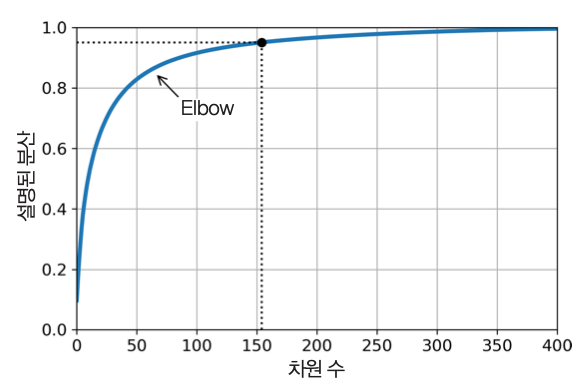
- 설명 분산 비율의 합과 차원 사이의 그래프 활용
- 설명 분산의 비율의 합의 증가가 완만하게 변하는 지점(elbow)에 주시할 것.
(MNIST 활용 예제) 압축을 위한 PCA¶
- PCA를 MNIST 데이터셋의 차원축소를 위해 사용할 수 있음.
- MINST 데이터셋의 주성분 분석을 통해 95% 정도의 분산을 유지하려면 154개 정도의 주성분만 사용해도 됨.
아래 코드: 154개 주성분 사용하여 차원축소하기
pca = PCA(n_components = 154) X_reduced = pca.fit_transform(X_train)
재구성 오차¶
- 차원축소 결과:
- 784차원을 154 차원으로 줄임.
- 유실된 정보: 5%
- 크기: 원본 데이터셋 크기의 20%
- 원본과의 비교: 정보손실 크지 않음 확인 가능

랜덤 PCA¶
- 주성분 선택을 위해 사용되는 SVD 알고리즘을 확률적으로 작동하도록 만드는 기법
- 보다 빠르게 지정된 개수의 주성분에 대한 근삿값을 찾아줌.
- $d$가 $n$ 보다 많이 작으면 기본 SVD 보다 훨씬 빠름.
- 기존의 특잇값 분해 알고리즘의 시간 복잡도: $O(m \times n^2) + O(n^3)$
- 랜덤 특잇값 분해 알고리즘의 시간 복잡도: $O(m \times d^2) + O(d^3)$
아래 코드:
svd_solver옵션을"randomized"로 설정rnd_pca = PCA(n_components = 154, svd_solver="randomized") X_reduced = rnd_pca.fit_transform(X_train)
점진적 PCA¶
- 훈련세트를 미니배치로 나눈 후 IPCA(점진적 PCA)에 하나씩 주입 가능
- 온라인 학습에 적용 가능
partial_fit()활용에 주의할 것.from sklearn.decomposition import IncrementalPCA n_batches = 100 inc_pca = IncrementalPCA(n_components=154) for X_batch in np.array_split(X_train, n_batches): inc_pca.partial_fit(X_batch) X_reduced = inc_pca.transform(X_train)
넘파이의 memmap() 클래스 활용 가능¶
- 바이너리 파일로 저장된 (매우 큰) 데이터셋을 마치 메모리에 들어있는 것처럼 취급할 수 있는 도구 제공
이를 이용하여 미니배치/온라인 학습 가능
X_mm = np.memmap(filename, dtype="float32", mode="readonly", shape=(m, n)) inc_pca = IncrementalPCA(n_components=154, batch_size=batch_size) inc_pca.fit(X_mm)
8.4 커널 PCA¶
커널 기법¶
- 5장의 커널 트릭을 이용한 기법
- PCA를 바로 실행하지 못하는 데이터셋을 보다 고차원으로 보낸 후 PCA를 실행하는 효과를 내는 기법. 실제로 고차원으로 보내지는 않음.
사영된 후에 샘플의 군집을 유지하거나 꼬인 다양체 모양의 데이터셋을 펼칠 때 유용.
from sklearn.decomposition import KernelPCA rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=0.04) X_reduced = rbf_pca.fit_transform(X)
롤케이크와 커널¶
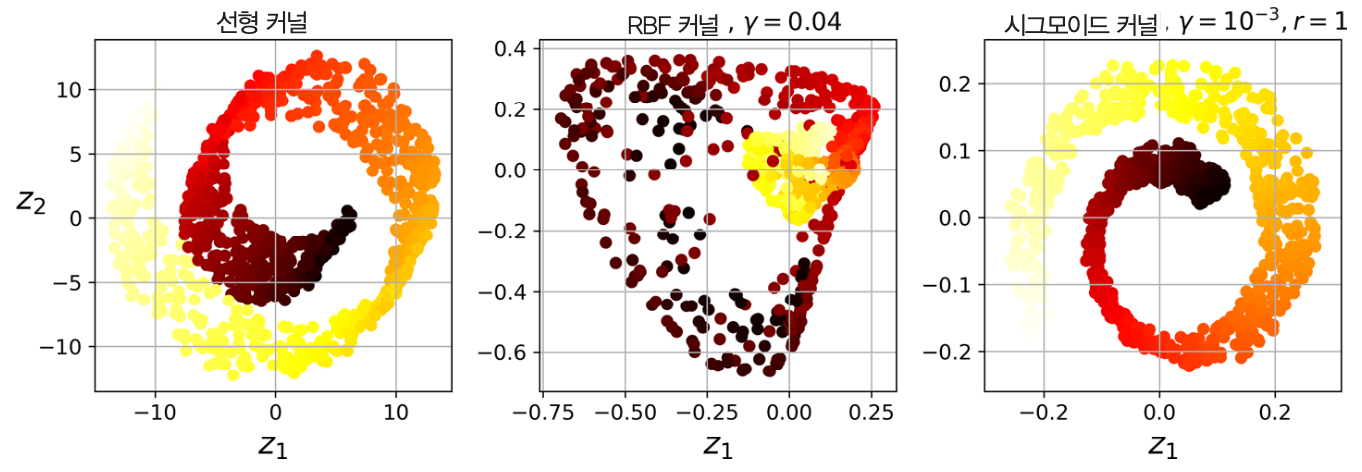
커널 선택과 하이퍼파라미터 튜닝¶
- kPCA는 기본적으로 비지도 학습.
- 참고: 차원축소 기법 일부는 지도학습임. 대표적인 예제는 LDA.
- 비지도 학습은 명확한 성능 측정 기준 없음.
- 하지만 ...
방식 1¶
전처리 용도로 사용 후 예측기와 연동하는 그리드탐색 등을 활용하여 성능 측정 가능
clf = Pipeline([ ("kpca", KernelPCA(n_components=2)), ("log_reg", LogisticRegression(solver="lbfgs")) ]) param_grid = [{ "kpca__gamma": np.linspace(0.03, 0.05, 10), "kpca__kernel": ["rbf", "sigmoid"] }] grid_search = GridSearchCV(clf, param_grid, cv=3) grid_search.fit(X, y)
방식 2¶
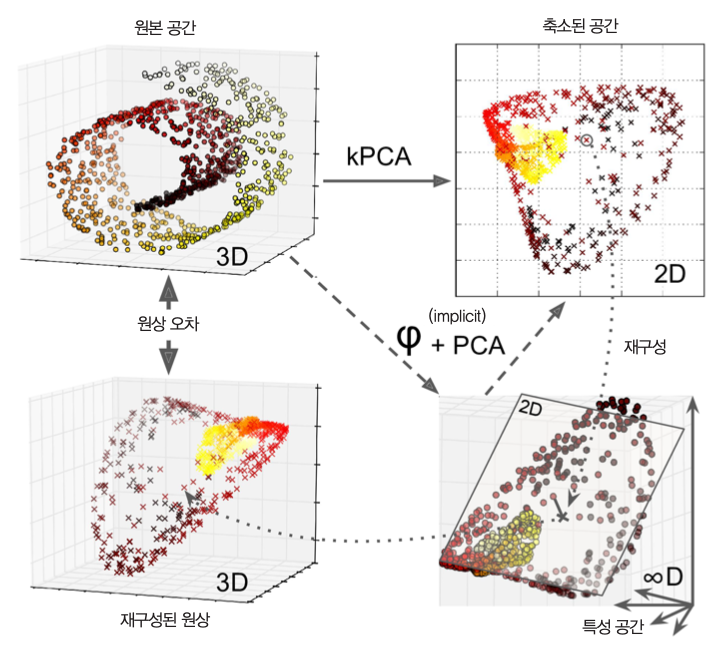
- 가장 낮은 재구성 오차를 만드는 커널과 하이퍼파라미터 선택 가능.
- 다만, kPCA의 재구성은 선형 PCA 보다 훨씬 어려움. 아래 그림 참조
8.5 LLE¶
LLE(국소적 선형 임베딩) 기본 아이디어¶
- 대표적인 다양체 학습 기법
- 롤케이크 데이터셋의 경우처럼 전체적으론 비선형인 다양체이지만 국소적으로는 데이터가 선형적으로 연관되어 있음.
- 국소적 관계가 가장 잘 보존되는 훈련 세트의 저차원 표현 찾을 수 있음.
- 사영이 아닌 다양체 학습에 의존
예제: 롤케이크¶
from sklearn.manifold import LocallyLinearEmbedding
lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10)
X_reduced = lle.fit_transform(X)
 |
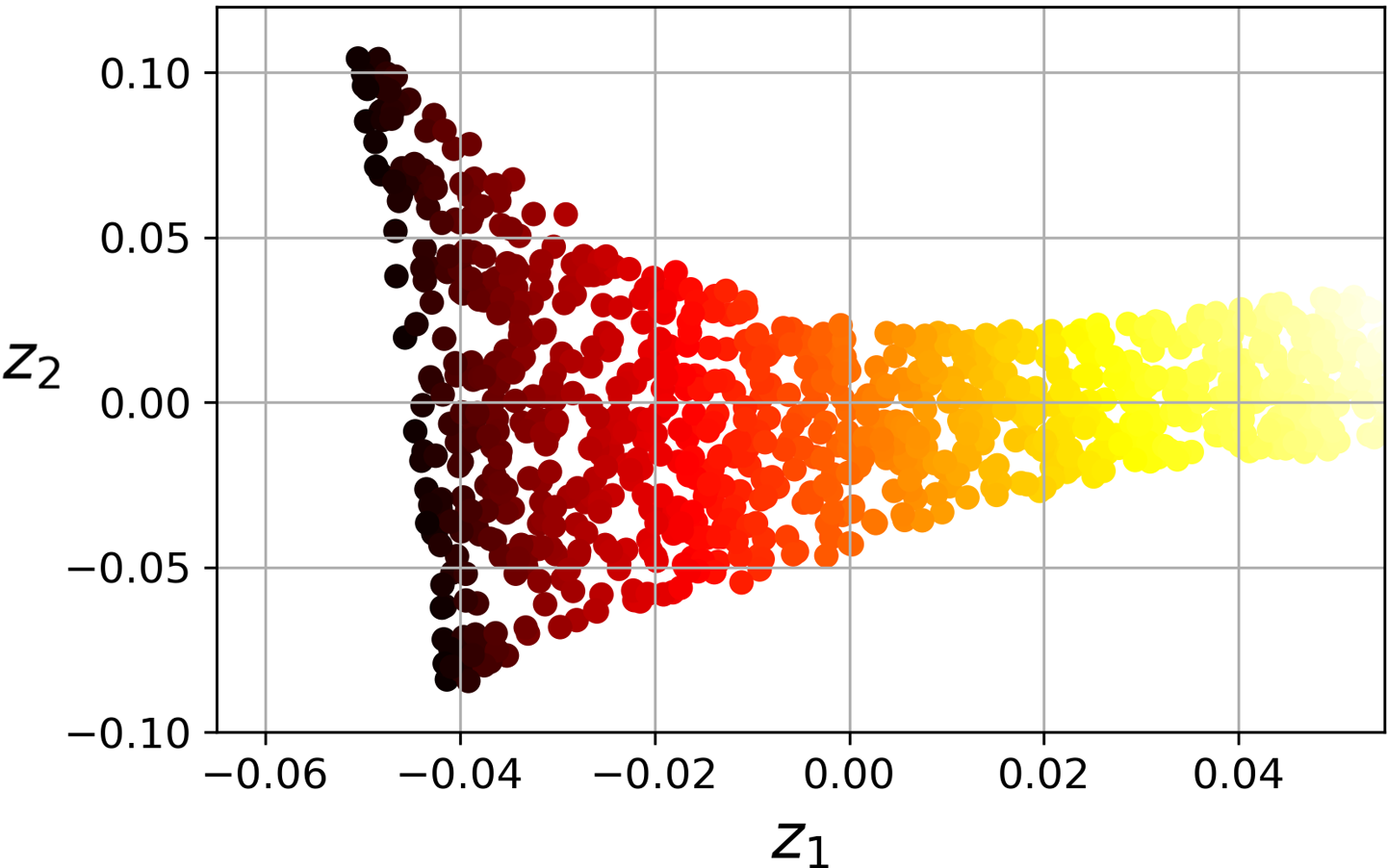 |
LLE 이론¶
다음 세 단계를 거쳐야 함.
$1$. 최근접 이웃 찾기: 지정된 숫자의 최근접 이웃 찾기
$2$. 가중치 행렬 찾기: 아래 최적화 문제를 해결하는 가중치 행렬 찾기
$$ \hat{\mathbf{W}} = \underset{\mathbf{W}}{\textrm{argmin}} \sum_{i=1}^{m} \left( \mathbf{x}^{(i)} - \sum_{j=1}^{m}w_{i,j}\, \mathbf{x}^{(j)} \right) $$단, 아래 조건 성립해야 함:
- $w_{i,j} = 0$: $\mathbf{x}^{(j)}$ 가 $\mathbf{x}^{(j)}$ 의 최근접 이웃이 아닐 때.
- $\sum_{j=1}^{m} = 1$: 모든 $i=1, 2, \dots, m$에 대해.
$3$. 아래 관계를 만족하는 최적의 $d$ 차원의 데이터셋 찾기
$$ \mathbf{Z} = \underset{\mathbf{Z}}{\textrm{argmin}} \sum_{i=1}^{m} \left( \mathbf{z}^{(i)} - \sum_{j=1}^{m}\hat{w}_{i,j}\, \mathbf{z}^{(j)} \right)^2 $$단, $\hat{w}_{i,j}$ 는 2단계에서 찾은 $\hat{\mathbf{W}}$의 항목임.
사이킷런의 LLE 모델 알고리즘¶
- 앞서 언급하 2단계를 해결하는 방식에 따라
LocallyLinearEmbedding모델의method옵션이 달라짐.
method옵션 종류:"statndard","modified","hessian","ltsa""statndard": 국소적 주성분 분석 아이디어를 활용하는 알고리즘. 기본값임."modified": 이웃 개수가 훈련 샘플의 차원보다 클 때 적용. 다중 가중치 벡터 활용."hessian": 헤세(Hesse)의 아이겐맵(Eigenmap)을 활용하는 알고리즘."ltsa": 국소적 접공간 설정(Local Tangent Space Alignment) 알고리즘.
- 시간복잡도: 알고리즘 마다 조금씩 다르다. 또한 3단계의 알고리즘이 $O(dm^2)$이기에 대용량의 훈련 세트에 부적절함.
8.6 기타 차원축소 기법¶
- 사영 기법
- 랜덤 사영
- 선형 판별 분석
- 다양체 학습
- 다차원 스케일링
- Isomap
- t-SNE
MNIST 데이터셋 시각화¶
- 다양한 차원축소 기법을 이용한 MNIST 데이터셋 시각화 가능
