6장 결정트리¶
감사의 글¶
자료를 공개한 저자 오렐리앙 제롱과 강의자료를 지원한 한빛아카데미에게 진심어린 감사를 전합니다.
주요내용¶
- 결정트리 훈련 방법과 시각화
- 클래스 예측 및 추정 확률
- CART 알고리즘 및 계산 복잡도
- 지니 불순도 vs. 엔트로피
- 규제 하이퍼파라미터
- 결정트리 회귀 모델
- 결정트리의 불안정성
6.1 결정트리 훈련 방법과 시각화¶
사이킷런의 결정트리 훈련¶
- 결정트리 방식의 최대 장점: 데이터 전처리 거의 불필요. 필요한 경우도 존재(불안정성 참조).
사이킷런의
DecisionTreeClassifier모델 활용- 붓꽃 데이터 활용. 꽃잎의 길이와 너비 기준으로 분류.
max_depth=2: 결정트리의 최대 깊이 지정. 여기서는 최대 2번의 데이터셋 분할 허용. 기본값은None이며 무제한 데이터셋 분할 허용.tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42) tree_clf.fit(X, y)
결정트리 시각화¶
- 사이킷런의
export_graphviz()함수 활용 - pdf, png 등 많은 종류의 파일로 변환 가능
- 주의사항: 파이썬 3.7 버전 사용해야 설치 가능
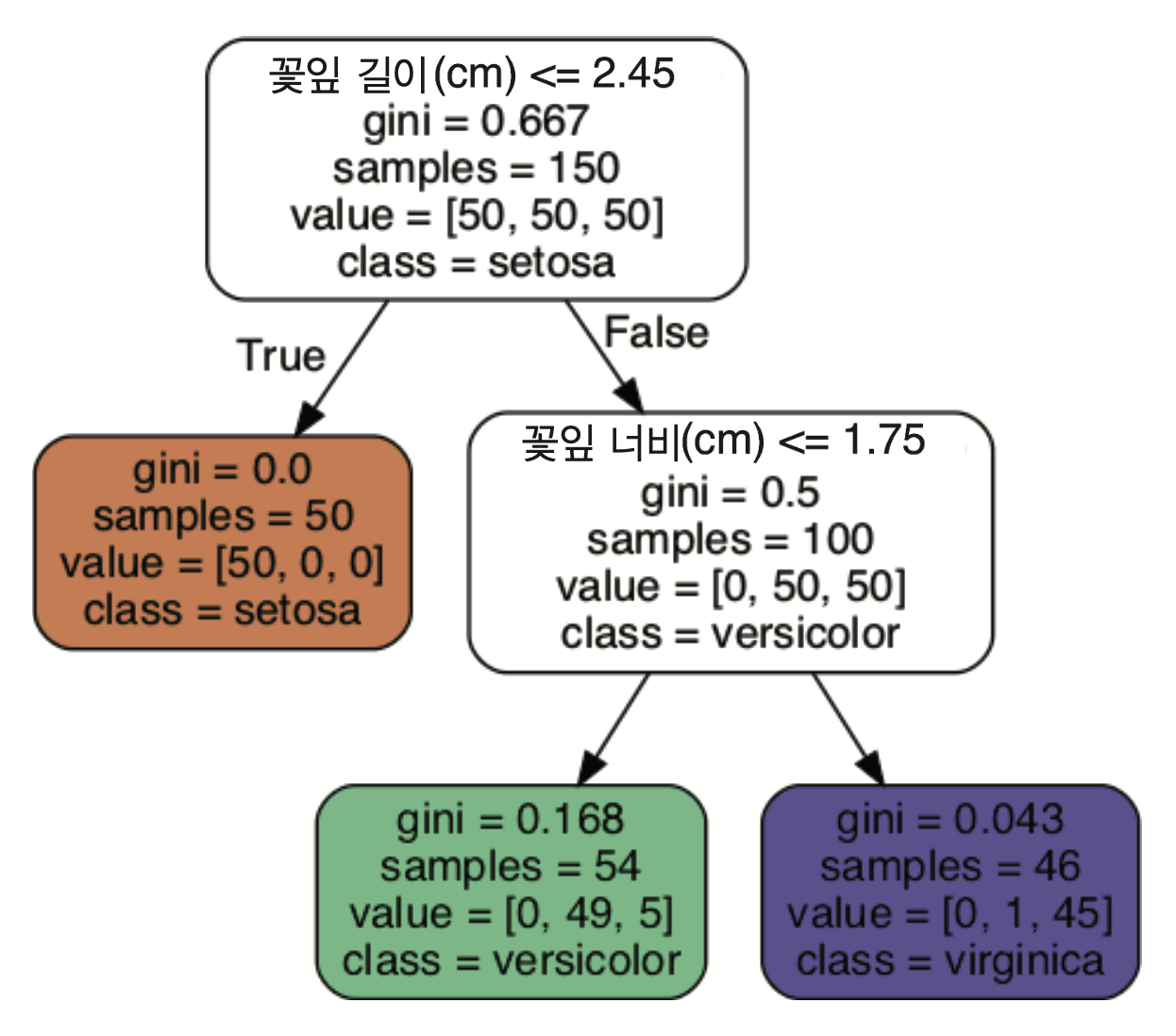
트리 구성 요소¶
- 노드(node): 가지 분할이 시작되는 지점
- 루트 노드(root node): 맨 상단에 위치한 노드
- 리프 노드(leaf node): 더 이상의 가지분할이 발생하지 않는 노드. 즉, 자식 노드가 없는 노드.
결정트리 노드의 속성¶
gini: 해당 노드의 지니 불순도 측정값- 모든 샘플이 동일 클래스에 속하면 불순도가 0이 됨. 즉,
gini=0.
- 모든 샘플이 동일 클래스에 속하면 불순도가 0이 됨. 즉,
samples: 해당 노드에 포함된 샘플 수
value: 해당 노드에 포함된 샘플들의 실제 클래스별 개수. 타깃 정보 활용됨.
class: 각 클래스별 비율을 계산하여 가장 높은 비율에 해당하는 클래스 선정- 동일한 비율이면 낮은 인덱스 선정
6.2 클래스 예측¶
예제¶
꽃잎 길이와 너비: 각각 5cm, 1.5cm
데이터가 주어지면 루트에서 시작
분할 1단계: 꽃잎 길이가 2.45cm 이하가 아니기에 오른편으로 이동.
분할 2단계: 꽃잎 너비가 1.75cm 이하이기에 왼편으로 이동. 버시컬러로 판정.
결정경계¶
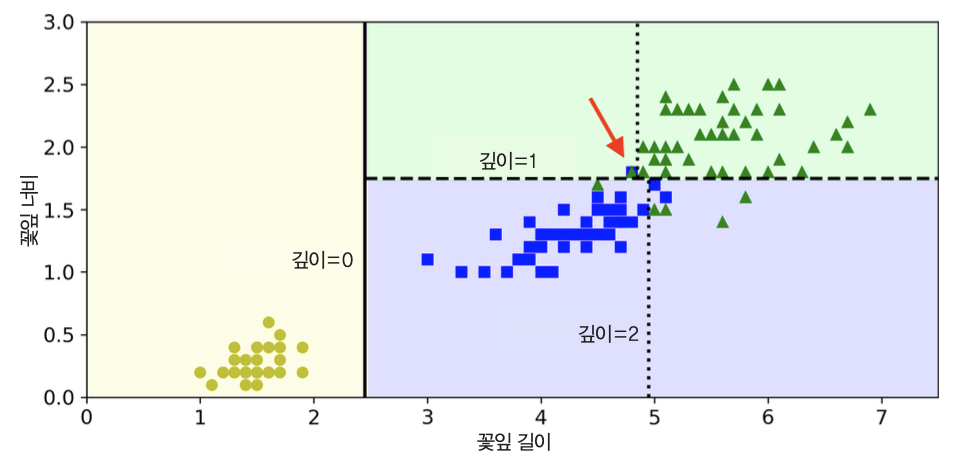
아래 그림은 max_depth=3으로 지정해서 학습한 결정트리의 결졍경계를 보여준다.
- 1차 분할 기준: 꽃잎 길이 2.45cm
- 2차 분할 기준: 꽃잎 너비 1.75cm
- 3차 분할 기준: 꽃잎 길이 4.85cm와 4.95cm
- 우상단 화살표가 가리키는 점, 세모와 네모가 겹쳐있음. 이 경우 과대적합으로 보아야 함.
6.3 클래스 추정 확률¶
클래스에 속할 확률 추정¶
- 주어진 샘플에 대해 예측된 노드에 속한 샘플들의 클래스별 비율
- 예제: 꽃잎 길이와 너비가 각각 5cm, 1.5cm인 붓꽃에 대한 클래스 추정 확률은 깊이 2의 왼편 노드에 포함된 샘플들의 클래스별 비율에서 최댓값으로 계산됨. 즉, 버시컬러에 속할 확률이 90.7%임.
- 참고: 동일한 노드에 속한 샘플에 대한 추정 확률은 언제나 동일
6.4 결정트리 훈련 알고리즘: CART¶
지니 불순도¶
불순도
$$G_i = 1 - \sum_{k=1}^{K} {p_{i,k}}^2$$
여기서 $p_{i,k}$는 $i$ 번째 노드에 있는 훈련 샘플 중 클래스 $k$에 속한 샘플의 비율임. $K$는 클래스의 수.
- 예제: 깊이 2의 왼편 노드의 지니 불순도는 0.168임.
CART(Classification and Regression Tree) 분류 알고리즘의 비용함수¶
- 각 노드에서 아래 비용함수를 최소화 하는 특성 $k$와 해당 특성의 임곗값 $t_k$을 결정해서 사용함.
- $m$, $m_\text{left}$, $m_\text{right}$: 각각 \부모와 자식 노드에 속한 샘플 수
- $G_\text{left}$, $G_\text{right}$: 두 자식 노드의 지니 불순도
$$
J(k, t_k) = \frac{m_\text{left}}{m}\, G_\text{left} + \frac{m_\text{right}}{m}\, G_\text{right}
$$
- $J(k, t_k)$가 작을수록 불순도가 낮은 두 개의 부분집합으로 분할됨
- 참고: 탐욕적 알고리즘 사용. 해당 노드를 기준으로 지니 불순도가 가장 낮은, 즉, 가장 순수한(pure) 두 개의 부분집합으로 분할함. 최적의 분할이란 보장은 없지만 일반적으로 적절한 성능을 보임.
- 분할 과정 반복:
max_depth등 규제의 한계에 다다르거나 더 이상 불순도를 줄이는 분할이 불가능할 때까지 진행.
6.5 CART 알고리즘의 계산 복잡도¶
최적의 결정트리 찾기¶
- 최적의 결정트리를 찾는 문제는 NP-완전(NP-complete)임.
- 이런 문제의 시간 복잡도는 $O(\exp(m))$
- 즉, 매우 작은 훈련 세트에 대해서도 제대로 적용하기 어려움
결정트리 모델의 예측 시간 복잡도¶
- 학습된 결정트리가 예측에 필요한 시간: $O(\log m)$
- 훈련 샘플 수 $m$에만 의존하며 매우 빠름. 각 노드에서 하나의 특성만 분류기준으로 사용되기에 특성 수와 무관하기 때문임.
CART 알고리즘의 시간 복잡도¶
- 훈련 샘플이 크기순으로 정렬된 경우 ($n, m$은 각각 특성 개수와 샘플 개수를 나타냄):
- 각 노드에서 분류하는 데 걸리는 시간: $O(n\cdot m\cdot \log(m))$
- 결정트리를 완성하는 데 걸리는 시간: $O(n\cdot m^2\cdot \log(m))$
- 규제가 있는 경우 좀 더 빨라짐.
DecisionTreeClassifier의presort=True옵션 설정: 훈련 세트를 먼저 정렬시킨 후 훈련 시작
- 훈련 세트의 크기가 몇 천보다 크면 정렬 자체가 오래 걸림. 가장 빠른 정렬 알고리즘의 복잡도가 $O(m\log m)$ 정도임.
6.6 지니 불순도 vs. 엔트로피¶
엔트로피 정의¶
DecisionTreeClassifier의criterion="entropy"옵션 설정:- gini 불순도 대신에 샘플들의 무질서 정도를 측정하는 엔트로피 사용
- 특정 노드의 엔트로피($H$) 계산
- 지니 불순도를 사용할 때와 비교해서 큰 차이가 나지 않음. 다만, 엔트로피 방식이 노드를 보다 균형 잡힌 두 개의 자식 노드로 분할함. 하지만 지니 불순도 방식이 보다 빠르게 훈련되며 따라서 기본값으로 사용됨.
엔트로피 방식의 장점 발생 이유¶
$$
\begin{align*}
& \text{특정 $k$에 대해 $p_k$가 0에 매우 가까운 경우} \\
&\quad\Rightarrow \text{$-\log(p_k)$가 매우 커짐} \\
&\quad\Rightarrow \text{엔트로피 증가} \\
&\quad\Rightarrow \text{비용함수 $J(k, t_k)$ 증가} \\
&\quad\Rightarrow \text{그런 조합은 피하게 됨} \\
&\quad\Rightarrow \text{보다 균형 잡힌 두 개의 부분집합으로 분할하는 방향으로 유도}
\end{align*}
$$
6.7 규제 하이퍼파라미터¶
비파라미터 모델¶
- 결정트리 모델은 데이터에 대한 어떤 가정도 하지 않음.
- 예를 들어, 노드를 분할할 수 있는 자유도(degree of freedom)에 대한 제한이 기본적으로 없음.
- 반면에 선형 모델 등은 데이터가 선형 모델을 따른다는 가정 등을 함.
- 이런 모델을 비파라미터 모델이라 함.
- 과대적합 위험 높음
사이킷런 DecisionTreeClassifier 규제하기¶
max_depth: 결정트리의 최대 높이 제한
min_samples_split: 노드를 분할하기 위해 필요한 최소 샘플 수
min_samples_leaf:리프 노드에 포함되어야 하는 최소 샘플 수
min_weight_fraction_leaf:- 샘플 별로 가중치가 설정된 경우: 가중치의 전체 합에서 해당 리프 노드에 포함된 샘플의 가중치의 합이 차지하는 비율
- 샘플 별로 가중치가 없는 경우:
min_samples_leaf와 동일한 역할 수행
max_leaf_nodes: 허용된 리프 노드의 최대 개수
max_features: 각 노드에서 분할 평가에 사용될 수 있는 최대 특성 수
- 규제를 높이는 방법
min_접두사 사용 규제: 값을 키울 것max_접두사 사용 규제: 값을 감소시킬 것
사이킷런 DecisionTreeClassifier 규제 사용¶
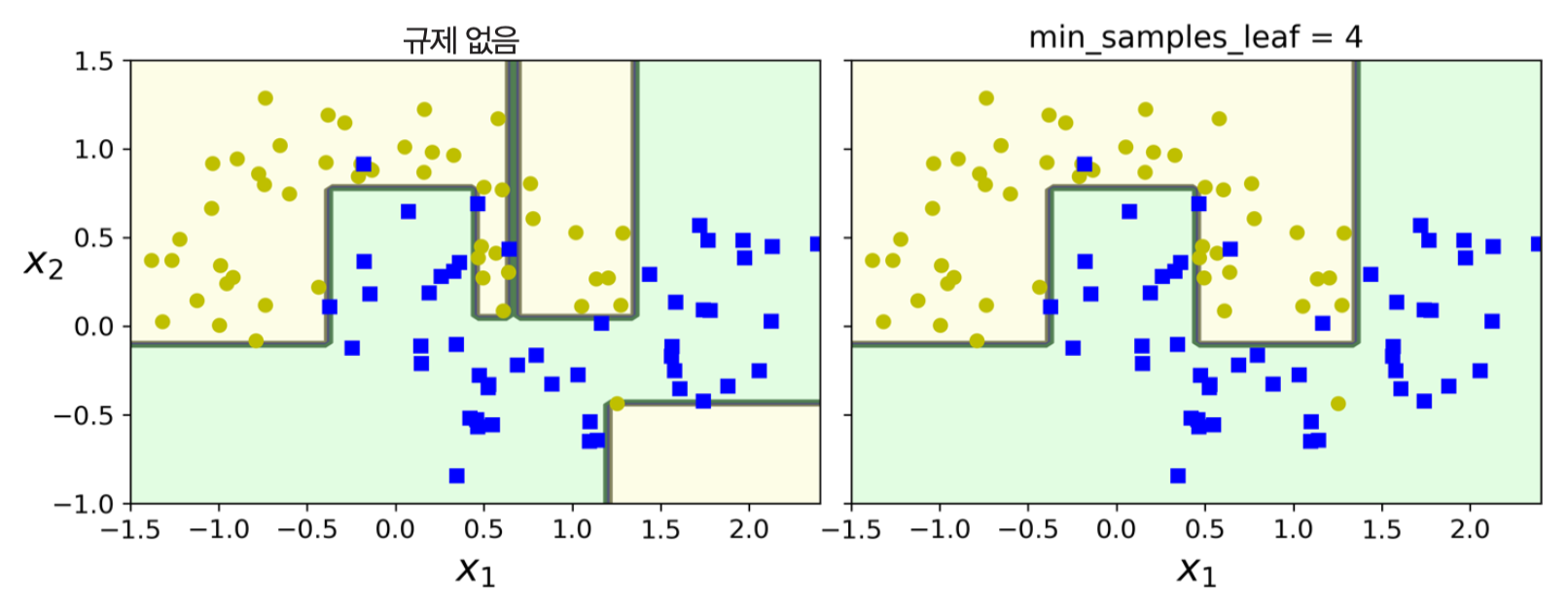
- 예제:
moons데이터셋에 대한 결정트리 모델 학습- 왼편: 규제 전혀 없음. 보다 정교하며 과대적합됨.
- 오른편:
min_samples_leaf=4. 일반화 성능이 보다 좋음.
6.8 (결정트리) 회귀¶
사이킷런의 DecisionTreeRegressor 예측기 활용¶
결정트리 알고리즘 아이디어를 거의 그대로 이용하여 회귀 문제에 적용 가능
tree_reg = DecisionTreeRegressor(max_depth=2, random_state=42) tree_reg.fit(X, y)
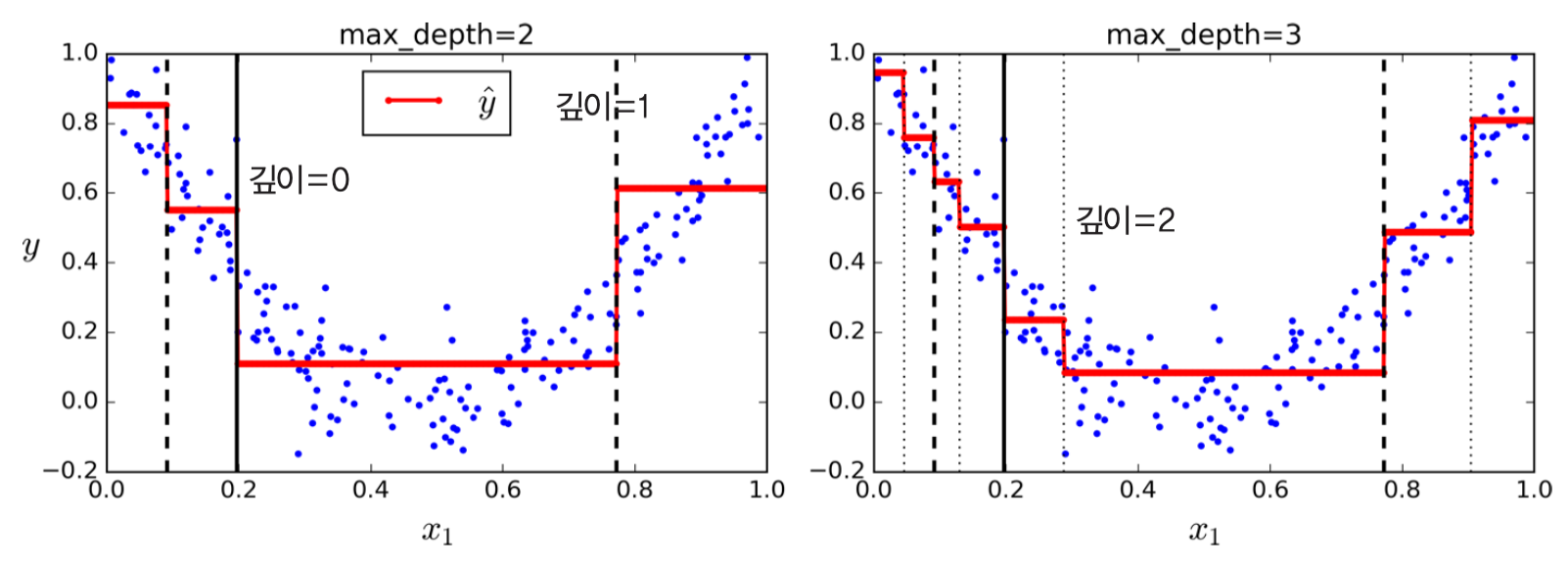
- 예제: 잡음이 포함된 2차 함수 형태의 데이터셋
- 왼편:
max_depth=2 - 오른편:
max_depth=3
- 왼편:
- 왼편 그림 설명
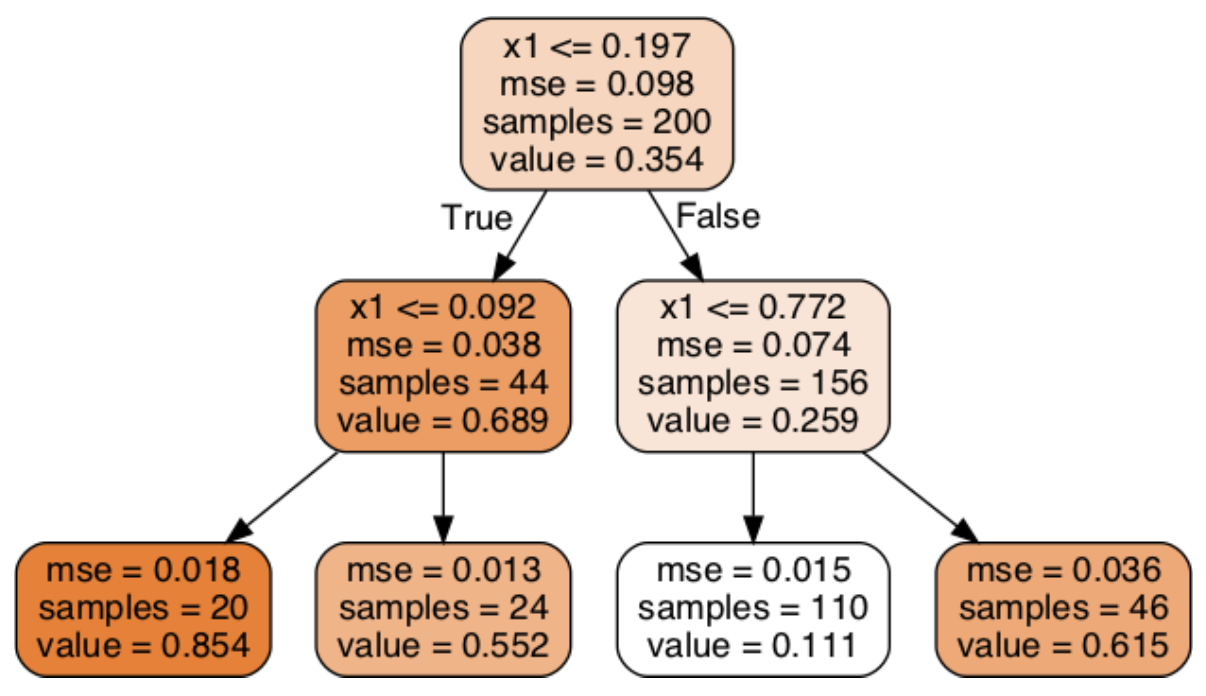
- 각 노드에 포함된 속성
samples: 해당 노드에 속한 훈련 샘플 수value: 해당 노드에 속한 훈련 샘플의 평균 타깃값mse: 해당 노드에 속한 훈련 샘플의 평균제곱오차(MSE)- 오차 기준은
value사용.
- 오차 기준은
회귀용 CART 알고리즘과 비용함수¶
- 분류의 경우처럼 탐욕적으로 아래 비용함수를 최소화 하는 특성 $k$와 해당 특성의 임곗값 $t_k$을 결정함:
$$
\begin{align*}
J(k, t_k) &= \frac{m_\text{left}}{m}\, \text{MSE}_\text{left} + \frac{m_\text{right}}{m}\, \text{MSE}_\text{right} \\[2ex]
\text{MSE}_\text{node} &= \sum_{i\in \text{node}} (\hat y_{node} - y^{(i)})^2\\[1ex]
\hat y_\text{node} &= \frac{1}{m_\text{node}} \sum_{i\in\text{node}} y^{(i)}
\end{align*}
$$
- $\text{MSE}_\text{left}$($\text{MSE}_\text{right}$):
지정된 특성 $k$와 특성 임곗값 $t_k$로 구분된 왼편(오른편) 부분집합의 평균제곱오차
- 해당 노드에 속한 샘플들의 평균 타깃값 기준
- $m_\text{left}$/$m_\text{right}$: 해당 노드에 속하는 샘플 수
- $y^{(i)}$: 샘플 $i$에 대한 실제 타깃
규제¶
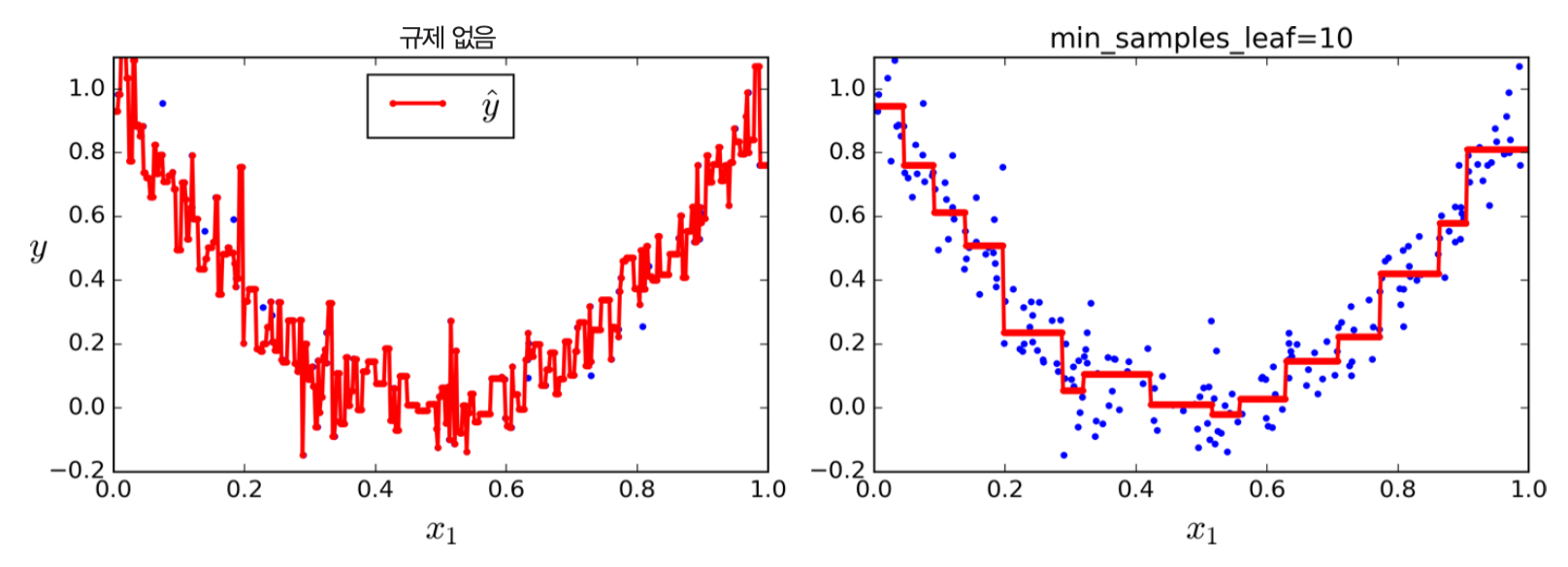
분류의 경우처럼 규제가 없으면 과대적합 발생할 수 있음.
왼편: 규제가 없는 경우. 과대적합 발생
오른편:
min_samples_leaf=10
6.9 (결정트리) 불안정성¶
단점 1: 훈련 세트 회전 민감도¶
- 결정트리 알고리즘은 성능이 매우 우수하지만 기본적으로 주어진 훈련 세트에 민감하게 반응함.
- 결정트리는 항상 축에 수직인 분할을 사용. 따라서 조금만 회전을 가해도 결정 경계가 많이 달라짐
- 예제: 오른편 그래프: 왼편 그래프를 45도 회전시킨 훈련 세트 학습
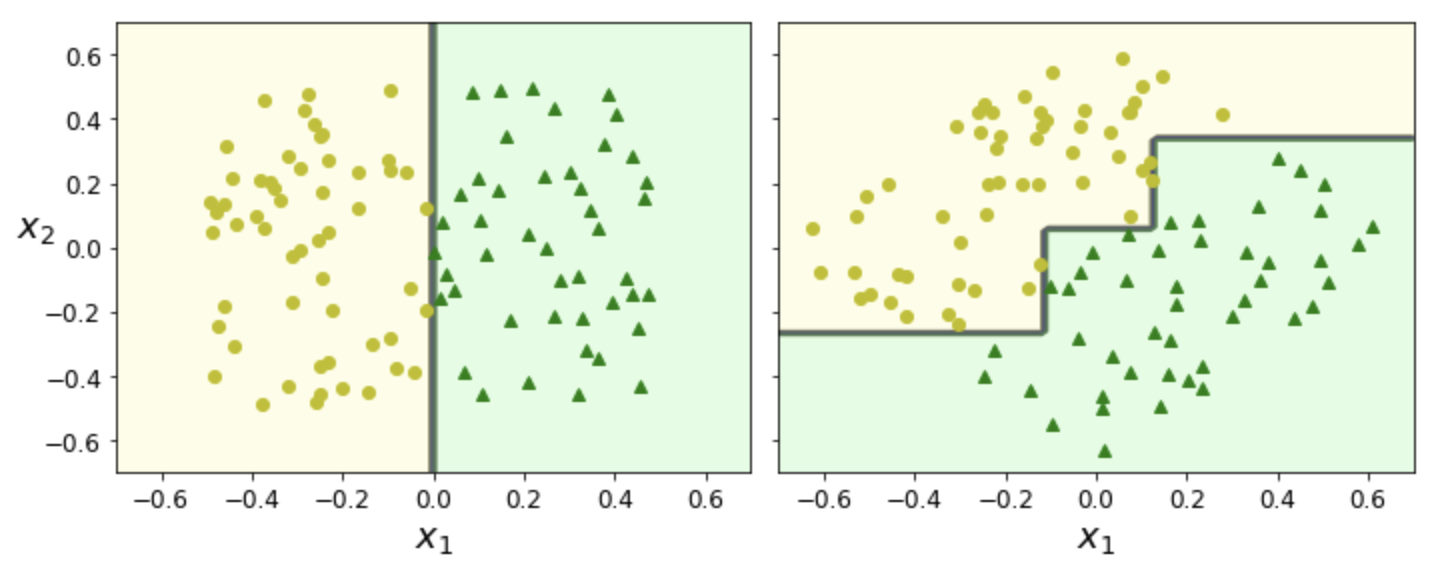
- PCA 기법 등을 사용하여 훈련 샘플 회전시킨 후 학습 가능. (8장 참조)
단점 2: 훈련 세트 변화 민감도¶
- 훈련 데이터의 작은 변화에도 매우 민감함.
- 예제: 붓꽃 데이터에서 하나의 샘플을 제거한 후 학습시킬 때 매우 다르게 학습할 수 있음.
- 왼편 그래프: 모든 샘플 대상 훈련
- 오른편 그래프: 가장 넓은 버시컬러 샘플 제거 후 훈련
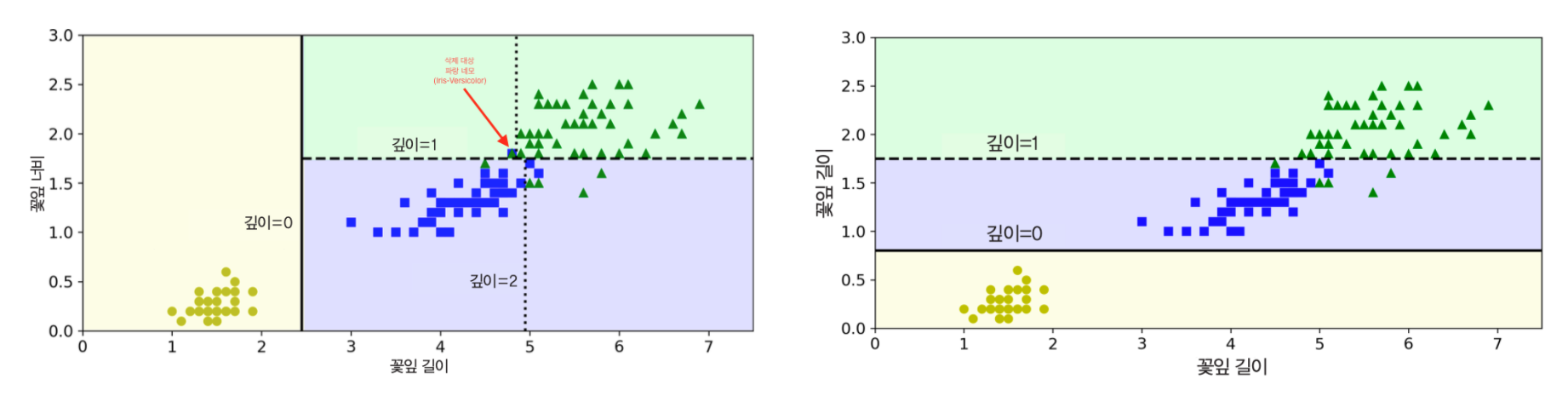
- 많은 트리에서 만든 예측값의 평균을 활용 추천(7장 램덤포레스트 모델 참조)