5장 서포트 벡터 머신 2부

감사의 글

자료를 공개한 저자 오렐리앙 제롱과 강의자료를 지원한 한빛아카데미에게 진심어린 감사를 전합니다.

주요 내용

1부

• 선형 SVM 분류

• 비선형 SVM 분류

2부

• SVM 회귀

• SVM 이론

5.3 SVM 회귀

SVM 분류 vs. SVM 회귀

• SVM 분류
  • 목표: 마진 오류 발생 정도를 조절(C 이용)하면서 두 클래스 사이의 도로폭을 최대한 넓게 하기
  • 마진 오류: 도로 위에 위치한 샘플

• SVM 회귀
  • 목표: 마진 오류 발생 정도를 조절(C 이용)하면서 지정된 폭의 도로 안에 가능한 많은 샘플 포함하기
  • 마진 오류: 도로 밖에 위치한 샘플
  • 참고: MathWorks: SVM 회귀 이해하기

선형 SVM 회귀

• 선형 회귀 모델을 SVM을 이용하여 구현

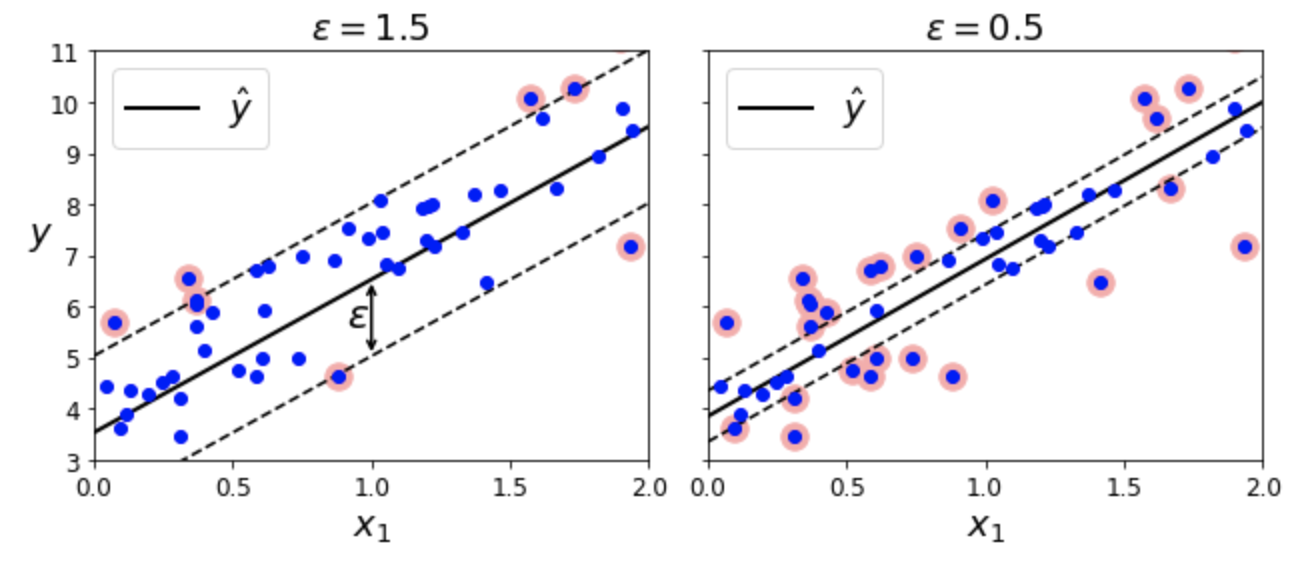
• 예제: LinearSVR 활용. epsilon은 도로폭 결정

  from sklearn.svm import LinearSVR
    svm_reg = LinearSVR(epsilon=1.5)
  

• 마진 안, 즉 결정 경계 도로 위에 포함되는 샘플를 추가해도 예측에 영향 주지 않음. 즉 epsilon에 둔감함.

비선형 SVM 회귀

• SVC와 동일한 커널 트릭을 활용하여 비선형 회귀 모델 구현

• 예제: SVR + 다항 커널

  # SVR + 다항 커널
    from sklearn.svm import SVR
  
    svm_poly_reg = SVR(kernel="poly", degree=2, C=100, epsilon=0.1, gamma="scale")
  

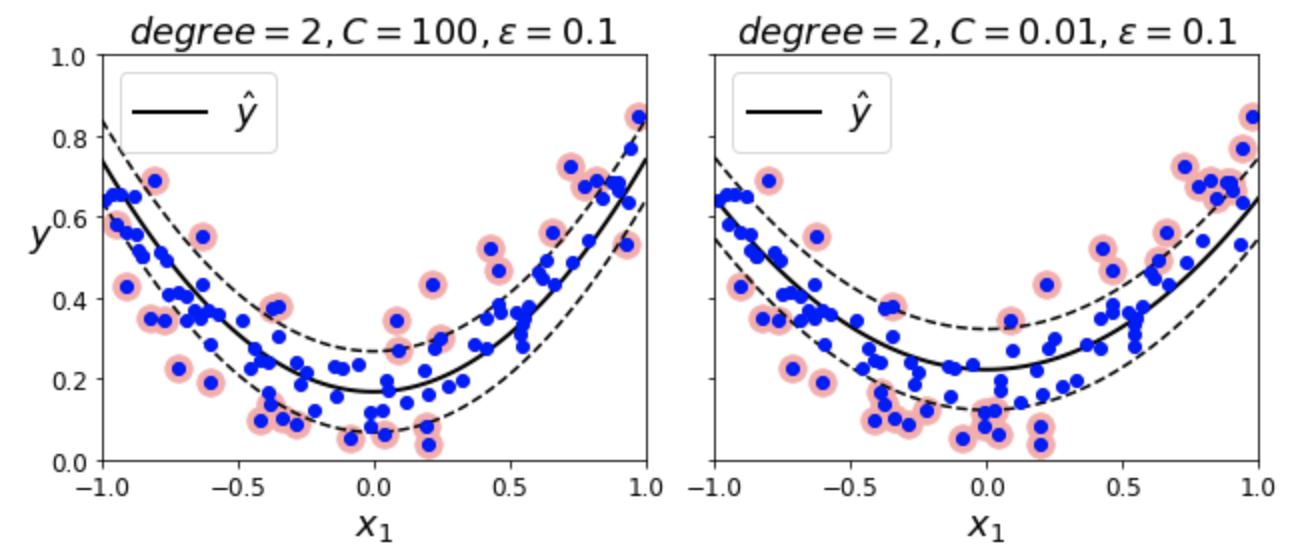
왼편 그래프(C=100)	오른편 그래프(C=0.01)
규제 보다 약함	규제 보다 강함
샘플에 덜 민감	샘플에 더 민감
마진 오류 보다 적게	마진 오류 보다 많이

회귀 모델 시간 복잡도

• LinearSVR: LinearSVC의 회귀 버전
  • 시간 복잡도가 훈련 세트의 크기에 비례해서 선형적으로 증가

• SVR: SVC의 회귀 버전
  • 훈련 세트가 커지면 매우 느려짐

5.4 SVM 이론

SVM 분류기의 결정 함수, 예측, 결정 경계, 목적함수

결정 함수와 예측

• 결정 함수: 아래 값을 이용하여 클래스 분류

$$ h(\mathbf x) = \mathbf w^T \mathbf x + b = w_1 x_1 + \cdots + w_n x_n + b $$

• 예측값: 결정 함수의 값이 양수이면 양성, 음수이면 음성으로 분류

$$ \hat y = \begin{cases} 0 & \text{if } h(\mathbf x) < 0\\ 1 & \text{if } h(\mathbf x) \ge 0 \end{cases} $$

결정 경계

• 결정 경계: 결정 함수의 값이 0인 점들의 집합

$$\{\mathbf x \mid h(\mathbf x)=0 \}$$

• 결정 경계 도로의 경계: 결정 함수의 값이 1 또는 -1인 샘플들의 집합

$$\{\mathbf{x} \mid h(\mathbf x)= \pm 1 \}$$

예제

붓꽃 분류. 꽃잎 길이와 너비를 기준으로 버지니카(Iris-Virginica, 초록 삼각형) 품종 여부 판단

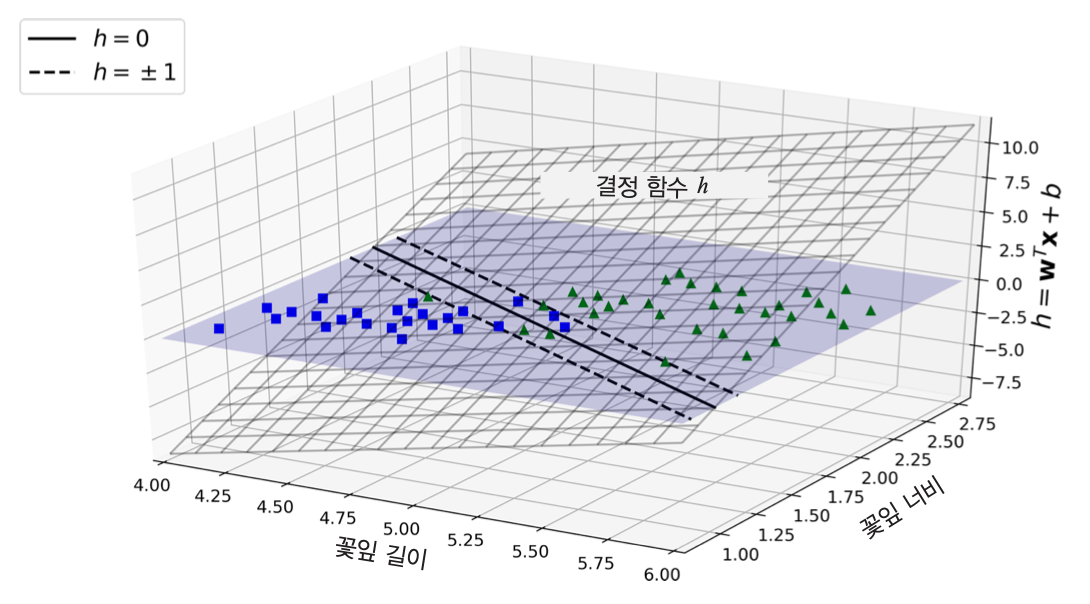
결정 함수의 기울기

• 결정 경계면(결정 함수의 그래프, 하이퍼플레인)의 기울기가 작아질 수록 도로 경계 폭이 커짐.

• 결정 경계면 기울기가 $\| \mathbf w \|$에 비례함. 따라서 결정 경계 도로의 폭을 크게 하기 위해 $\| \mathbf w \|$를 최소화해야 함.

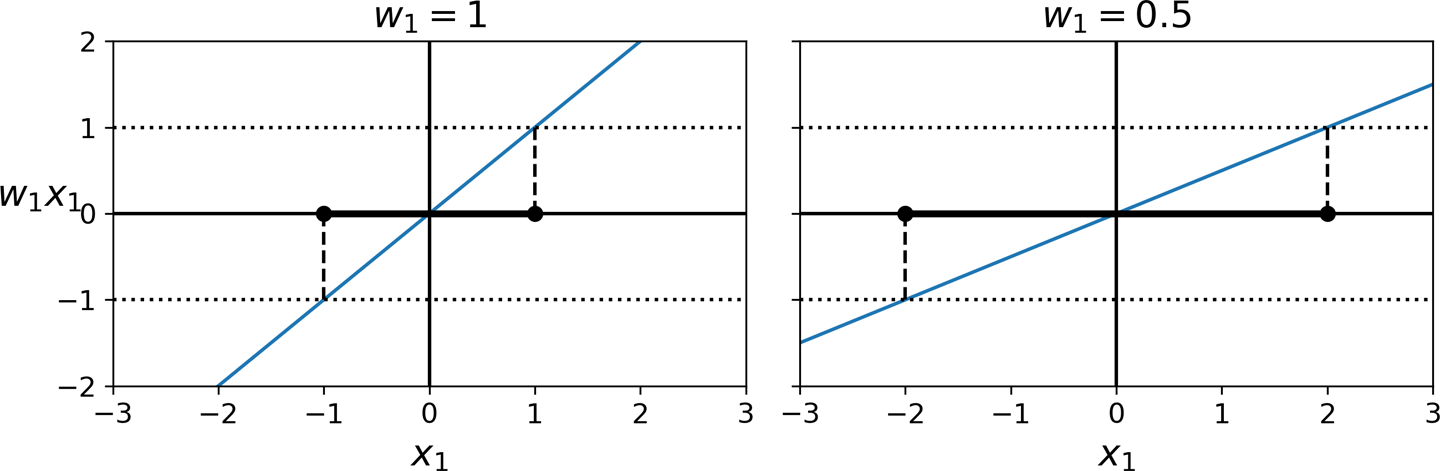
• 하드 마진 모델 훈련: 모든 양성(음성) 샘플이 결정 경계 도로 밖에 위치하도록 하는 기울기 찾기.

• 소프트 마진 모델 훈련: 결정 경계 도로 위에 위치하는 샘플의 수를 제한하면서 결정 경계 도로의 폭이 최대가 되도록 하는 기울기 찾기.

목적함수

• 결정 경계면의 기울기 $\| \mathbf w \|$를 최소화하는 것과 아래 식을 최소화하는 것이 동일한 의미임. 따라서 아래 식을 목적함수로 지정함.

$$\frac 1 2 \| \mathbf w \|^2 = \frac 1 2 \mathbf w^T \mathbf w$$

• 이유: 함수의 미분가능성 때문에 수학적으로 다루기가 보다 쉬움. $1/2$ 또한 계산의 편의를 위해 추가됨.

하드 마진 선형 SVM 분류기의 목적 함수

• 목적함수를 최소화하는 파라미터 벡터 $\mathbf{w}$를 구하기 위해 다음 최적화 문제를 해결해야 함.

$$\frac 1 2 \mathbf w^T \mathbf w$$$$ \text{(조건)}\quad t^{(i)} (\mathbf w^T \mathbf x^{(i)} + b) \ge 1 $$

• 즉, 모든 샘플 $\mathbf{x}^{(i)}$에 대해 만족시켜야 하는 조건이 추가되었음. $t^{(i)}$는 $i$ 번째 샘플의 클래스(양성/음성)를 가리킴.

$$ t^{(i)} = \begin{cases} -1 & \text{$x^{(i)}$가 음성인 경우} \\ 1 & \text{$x^{(i)}$가 양성인 경우} \end{cases} $$

조건식의 의미

$$ \text{(조건)}\quad t^{(i)} (\mathbf w^T \mathbf x^{(i)} + b) \ge 1 $$

위 조건식의 의미는 다음과 같다.

• $\mathbf x^{(i)}$가 양성인 경우
  • $t^{(i)} = 1$
  • 따라서 $\mathbf w^T \mathbf x^{(i)} + b \ge 1$, 즉 양성으로 예측해야 함.

• $\mathbf x^{(i)}$가 음성인 경우
  • $t^{(i)} = -1$
  • 따라서 $\mathbf w^T \mathbf x^{(i)} + b \le -1$, 즉 음성으로 예측해야 함.

소프트 마진 선형 SVM 분류기의 목적 함수

• 목적함수와 조건이 다음과 같음.

$$\frac 1 2 \mathbf w^T \mathbf w + C \sum_{i=0}^{m-1} \zeta^{(i)}$$

$$\text{(조건)}\quad t^{(i)} (\mathbf w^T \mathbf x^{(i)} + b) \ge 1 - \zeta^{(i)}$$

• $\zeta^{(i)}\ge 0$: 슬랙 변수. $i$ 번째 샘플에 대한 마진 오류 허용 정도 지정. ($\zeta$는 그리스어 알파벳이며 '체타(zeta)'라고 발음함.)

• $C$: 아래 두 목표 사이의 트레이드오프를 조절하는 하이퍼파라미터
  • 목표 1: 결정 경계 도로의 폭을 가능하면 크게 하기 위해 $\|\mathbf w\|$ 값을 가능하면 작게 만들기.
  • 목표 2: 마진 오류 수를 제한하기, 즉 슬랙 변수의 값을 작게 유지하기.

• 참고: 결정 경계 도로의 폭, 즉 마진 폭은 결정 경계면($\hat y = \mathbf{w}^T \mathbf{x} + b$)의 기울기 $\|\mathbf w\|$ 에 의해 결정됨

$\zeta$의 역할

• $\zeta^{(i)} > 0$이면 해당 샘플 $\mathbf{x}^{(i)}$에 대해 다음이 성립하여 마진 오류가 될 수 있음.

  $$1 - \zeta^{(i)} \le t^{(i)} (\mathbf w^T \mathbf x^{(i)} + b) < 1$$

• 이유: 결정 경계면(하이퍼플레인) 상에서 보면 결정 함숫값이 $1$보다 작은 샘플이기에 실제 데이터셋의 공간에서는 결정 경계 도로 안에 위치하게 됨. (결정 경계 도로의 양 경계는 결정 함숫값이 $1$인 샘플들로 이루어졌음.)

C와 마진 폭의 관계 (1부)

$$\frac 1 2 \mathbf w^T \mathbf w + C \sum_{i=0}^{m-1} \zeta^{(i)}$$

$$\text{(조건)}\quad t^{(i)} (\mathbf w^T \mathbf x^{(i)} + b) \ge 1 - \zeta^{(i)}$$

• 가정: 보다 간단한 설명을 위해 편향 $b$는 $0$이거나 무시될 정도로 작다고 가정. (표준화 전처리를 사용하면 됨.)

• $C$가 매우 큰 경우
  • $\zeta$는 $0$에 매우 가까울 정도로 아주 작아짐.
  • 예를 들어 양성 샘플 $\mathbf{x}^{(i)}$에 대해, 즉 $t^{(i)} = 1$, $\mathbf{w}^T \mathbf{x}^{(i)}$ 가 $1$보다 크거나 아니면 $1$보다 아주 조금만 작아야 함. 즉, 결정 경계면의 기울기 $\|w\|$가 어느 정도 커야 함.
  • 결정 경계의 도로폭이 좁아짐.

C와 마진 폭의 관계 (2부)

$$\frac 1 2 \mathbf w^T \mathbf w + C \sum_{i=0}^{m-1} \zeta^{(i)}$$

$$\text{(조건)}\quad t^{(i)} (\mathbf w^T \mathbf x^{(i)} + b) \ge 1 - \zeta^{(i)}$$

• $C$가 매우 작은 경우
  • $\zeta$가 어느 정도 커도 됨.
  • $\mathbf{w}^T \mathbf{x}^{(i)}$ 가 1보다 많이 작아도 됨. 즉, $\|w\|$ 가 작아도 됨.
  • 결정 경계의 도로폭이 넓어짐.

커널 SVM 작동 원리

쌍대 문제

• 쌍대 문제(dual problem): 주어진 문제의 답과 동일한 답을 갖는 문제

• 선형 SVM 목적 함수의 쌍대 문제: 아래 식을 최소화하는 $\alpha$ 찾기(단, $\alpha^{(i)} > 0$).

$$ \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha^{(i)}\alpha^{(j)} t^{(i)} t^{(j)} {\mathbf{x}^{(i)}}^T\mathbf{x}^{(j)} - \sum_{j=1}^{m} \alpha^{(i)} $$

쌍대 문제 활용 예제: 다항 커널

• 원래 $d$차 다항식 함수 $\phi()$를 적용한 후에 쌍대 목적 함수의 최적화 문제를 해결해야 함. 즉, 아래 문제를 최소화하는 $\alpha$를 찾는 게 쌍대문제임.

$$ \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha^{(i)}\alpha^{(j)} t^{(i)} t^{(j)} \phi(\mathbf{x}^{(i)})^T \phi(\mathbf{x}^{(j)}) - \sum_{j=1}^{m} \alpha^{(i)} $$

• 하지만 다음이 성립함.

$$ \phi(\mathbf a)^T \phi(\mathbf b) = ({\mathbf a}^T \mathbf b)^d $$

• 따라서 다항식 함수 $\phi$를 적용할 필요 없이, 즉 다항 특성을 전혀 추가할 필요 없이 아래 함수에 대한 최적화 문제를 해결하면 다항 특성을 추가한 효과를 얻게 됨.

$$ \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha^{(i)}\alpha^{(j)} t^{(i)} t^{(j)} \left({\mathbf{x}^{(i)}}^T\mathbf{x}^{(j)}\right)^d - \sum_{j=1}^{m} \alpha^{(i)} $$

예제: 지원되는 커널

• 다항식:

$$K(\mathbf a, \mathbf b) = \big( \gamma \mathbf a^T \mathbf b + r \big)^d$$

• 가우시안 RBF:

$$K(\mathbf a, \mathbf b) = \exp \big( \!-\! \gamma \| \mathbf a - \mathbf b \|^2 \big )$$

온라인 SVM

• 경사하강법을 이용하여 선형 SVM 분류기를 직접 구현할 수 있음.

• 비용함수는 아래와 같음.

$$ J(\mathbf{w}, b) = \dfrac{1}{2} \mathbf{w}^T \mathbf{w} \,+\, C {\displaystyle \sum_{i=1}^{m}\max\left(0, 1 - t^{(i)}(\mathbf{w}^T \mathbf{x}^{(i)} + b) \right)} $$

• 자세한 내용은 주피터 노트북의 부록 B 참조: [html], [구글 코랩]