5장 서포트 벡터 머신 1부¶

감사의 글¶

자료를 공개한 저자 오렐리앙 제롱과 강의자료를 지원한 한빛아카데미에게 진심어린 감사를 전합니다.

주요 내용¶

1부¶

  • 선형 SVM 분류
  • 비선형 SVM 분류

2부

  • SVM 회귀

  • SVM 이론

5.1 선형 SVM 분류¶

기본 아이디어¶

  • 마진(margin): 클래스를 구분하는 도로의 경계

  • 라지 마진 분류: 마진 폭을 최대로 하는 클래스 분류

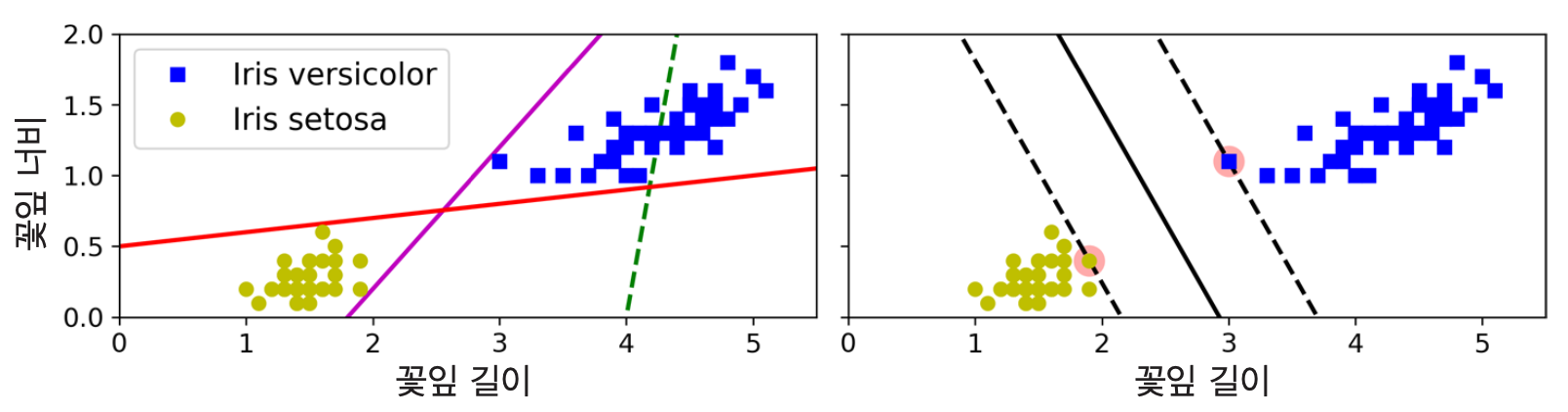
왼편 그래프 오른편 그래프
분류기: 선형 분류 라지 마진 분류
실선: 결정 경계 결정 경계
일반화: 일반화 어려움 일반화 쉬움

서포트 벡터¶

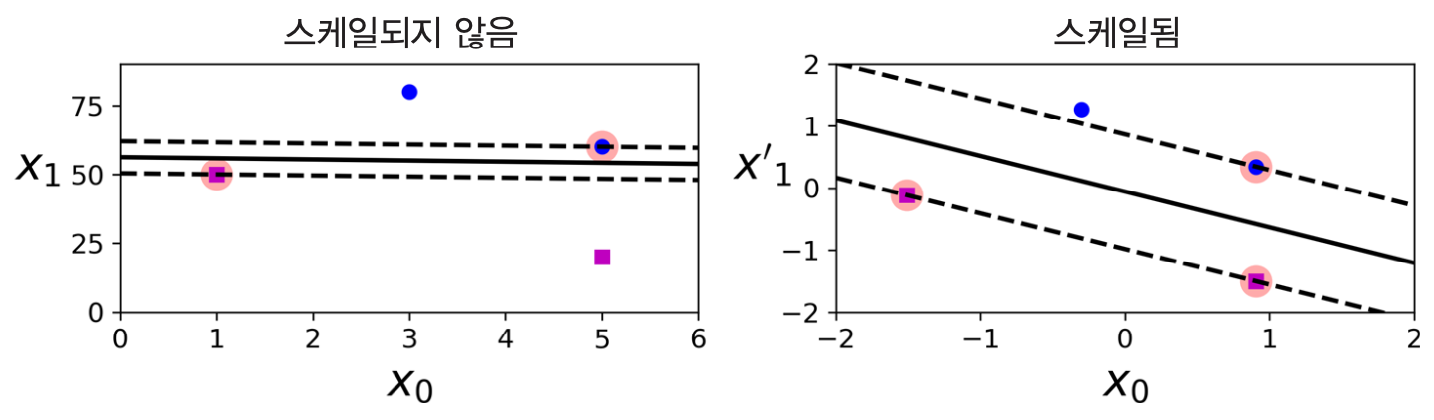
  • 도로의 양쪽 경계에 위치하는 샘플 (아래 그림에서 동그라미 표시됨)
  • 서포트 벡터 사이의 간격, 즉 도로의 폭이 최대가 되도록 학습
  • 특성 스케일을 조정하면 결정경계가 훨씬 좋아짐.

서포트 벡터 머신(SVM) 모델¶

  • 두 클래스로부터 최대한 멀리 떨어져 있는 결정 경계를 찾는 분류기
  • 목표: 특정 조건을 만족하면서 동시에 클래스를 분류하는 가능한 넒은 도로의 결정 경계 찾기

하드 마진 분류¶

  • 모든 훈련 샘플이 도로 바깥쪽에 올바르게 분류되도록 하는 마진 분류
  • 훈련 세트가 선형적으로 구분되는 경우에만 가능
  • 이상치에 민감함
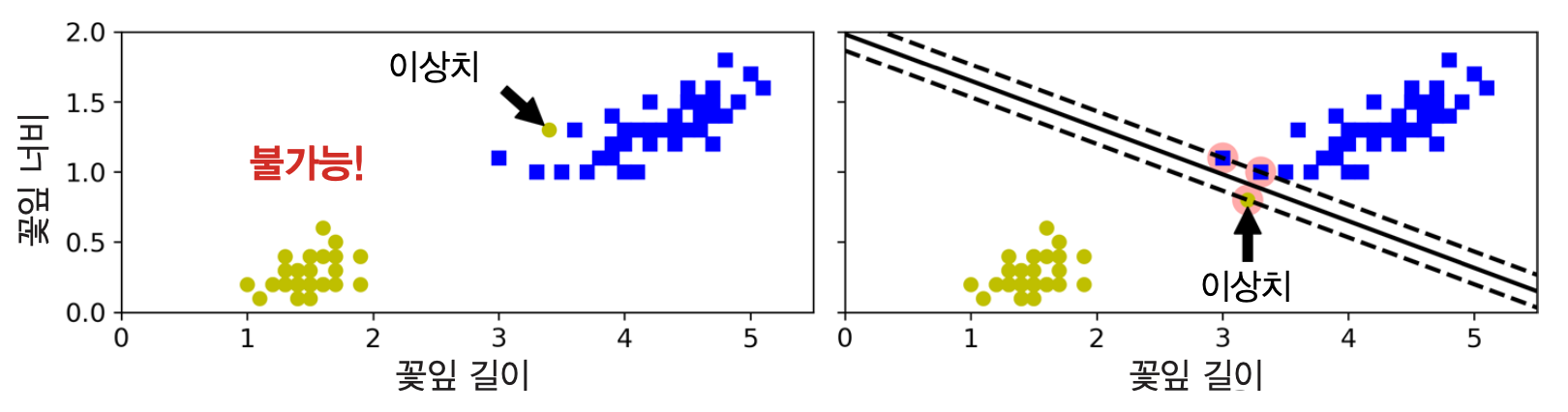
왼편 그래프 오른편 그래프
이상치: 타 클래스에 섞임 타 클래스에 매우 가까움
하드 마진 분류: 불가능 가능하지만 일반화 어려움

소프트 마진 분류¶

  • 마진 오류(margin violation) 사례의 발생 정도를 조절하면서 도로의 폭을 최대로 넓게 유지하는 마진 분류
  • 마진 오류: 훈련 샘플이 도로 상에 위치하거나 결정 경계를 넘어 해당 클래스 반대편에 위치하는 샘플
  • 하드 마진 분류 불가능 예제: 꽃잎 길이와 너비 기준의 버지니카와 버시컬러 품종

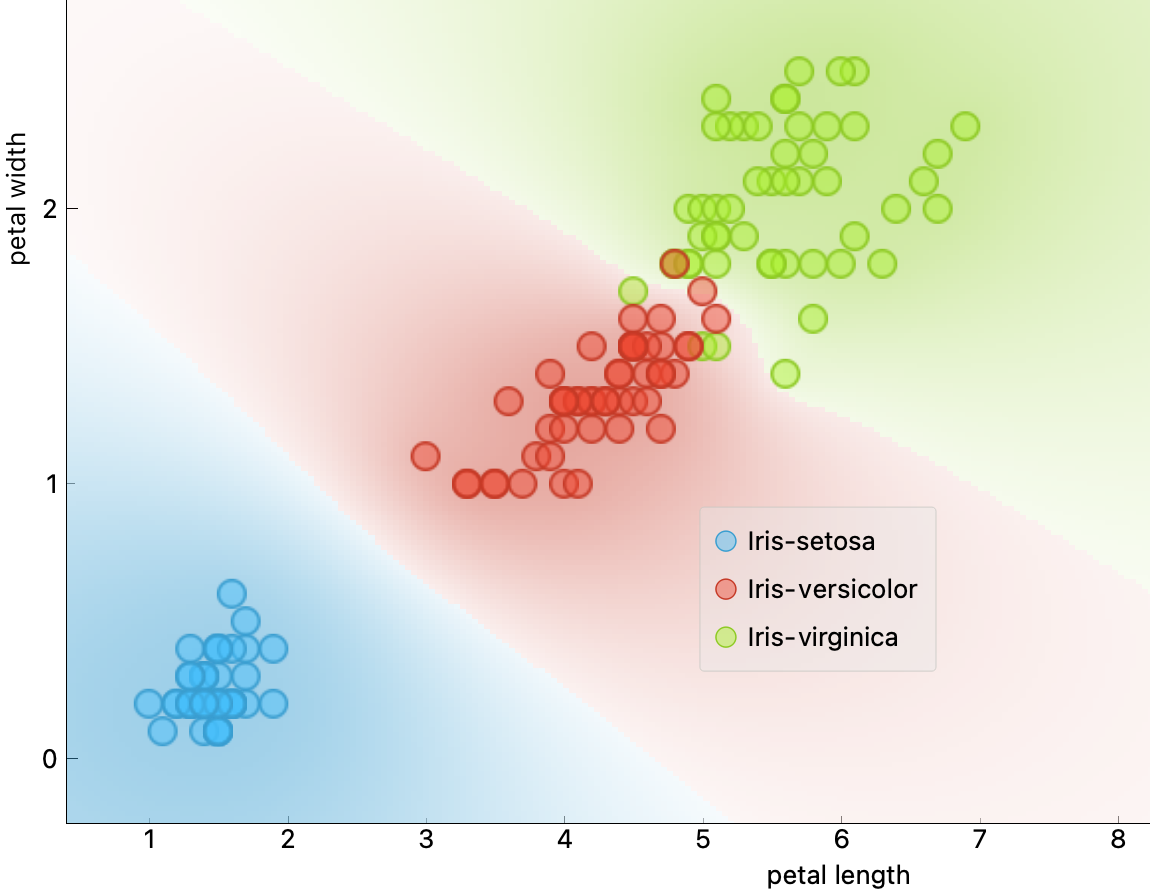
예제: 버지니까 품종 여부 판단¶

  • 사이킷런의 선형 SVM 분류기 LinearSVC 활용

    svm_clf1 = LinearSVC(C=1, loss="hinge", random_state=42)
  • C: 무조건 양수이어야 하며 클 수록 마진 오류를 적게, 즉 도로폭을 작게 만듦. 결국 C가 클 수록 규제를 덜 가하게 되어 모델의 자유도를 올려 과대적합 가능성을 키움. 또한 C=float("inf")로 지정하면 하드 마진 분류 모델이 됨.
  • hinge: 힌지 손실. 예측값과 실제 라벨 사이의 차이가 클 수록 큰 손실이 가해짐.
  • dual=True: 쌍대성(duality) 이용 여부. True가 기본. 하지만 특성 수가 샘플 수보다 작을 때는 False 권장.
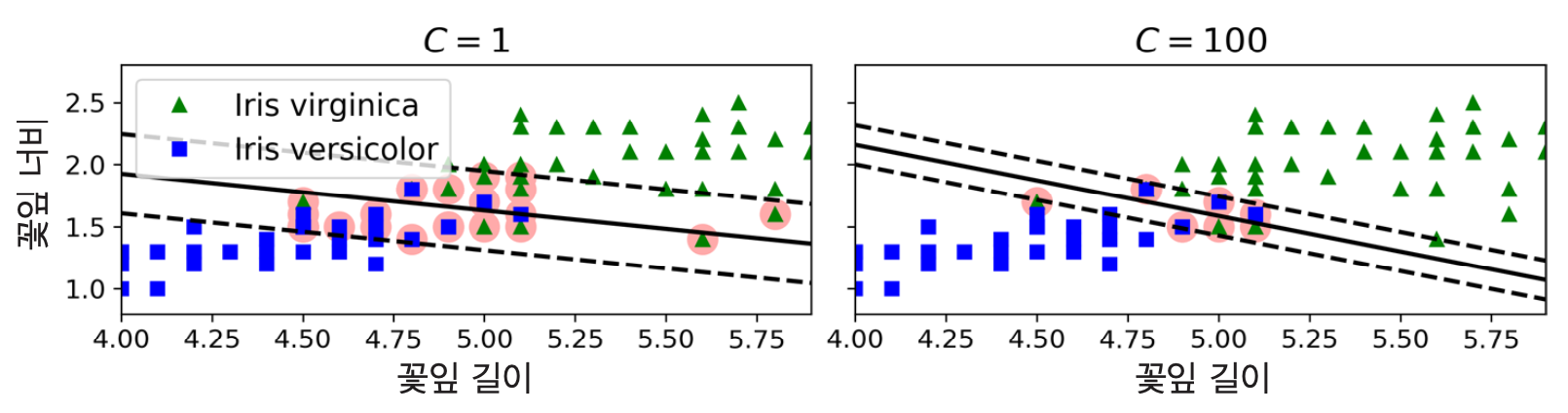
왼편 그래프 오른편 그래프
C 작게 크게
도로폭(마진 오류 수) 크게 작게
분류 덜 정교하게 보다 정교하게

스케일 조정의 중요성¶

  • LinearSVC 모델의 경우 편향도 규제 대상임. 따라서 평균을 빼서 0으로 편향을 없애는 것이 중요. 하지만 표준화 스케일링을 하면 자연스럽게 해결됨.
  • 반면에 SVC 모델은 편향을 규제하지는 않음. 그럼에도 불구하고 기본적으로 표준화 스케일링을 진행하는 것이 보다 좋은 성능의 모델을 훈련시킴.
  • 이전의 두 그림 모두 표준화 스케일링 전처리를 한 후에 학습을 시킨 모델임.

기타 선형 SVM 지원 모델 예제 (주피터 노트북 부록 B 참조)¶

  • 선형 분류는 LinearSVC 모델이 제일 빠름. 하지만 'SVC + 선형 커널' 조합도 사용 가능.

    SVC(kernel="linear", C=1)

  • SGDClassifier + hinge 손실함수 활용 + 규제: 규제 강도가 훈련 샘플 수(m)에 반비례.

    SGDClassifier(loss="hinge", alpha=1/(m*C))
  • hinge 손실 함수: 어긋난 예측 정도에 비례하여 손실값이 선형적으로 커짐.

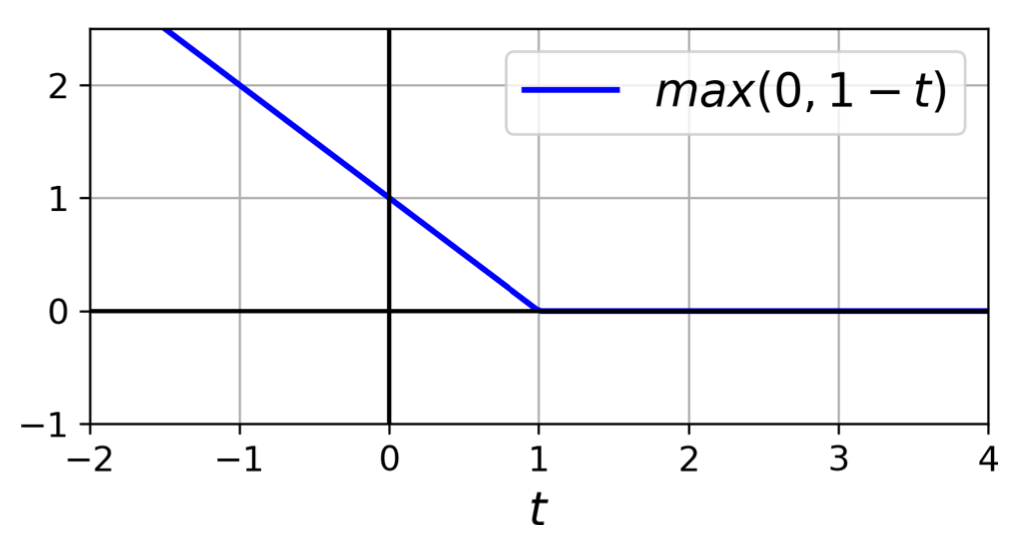
5.2 비선형 분류¶

  • 방식 1: 특성 추가 + 선형 SVC
    • 다항 특성 활용: 다항 특성을 추가한 후 선형 SVC 적용
    • 유사도 특성 활용: 유사도 특성을 추가한 후 선형 SVC 적용
  • 방식 2: SVC + 커널 트릭
    • 커널 트릭: 새로운 특성을 실제로 추가하지 않으면서 동일한 결과를 유도하는 방식
    • 예제 1: 다항 커널 (주의: 책에서는 다항식 커널로 불림)
    • 예제 2: 가우시안 RBF(방사 기저 함수) 커널

5.2.1 다항 커널¶

다항 특성 추가 + 선형 SVM¶

  • 예제 1: 특성 $x_1$ 하나만 갖는 모델에 새로운 특성 $x_1^2$을 추가한 후 선형 SVM 분류 적용

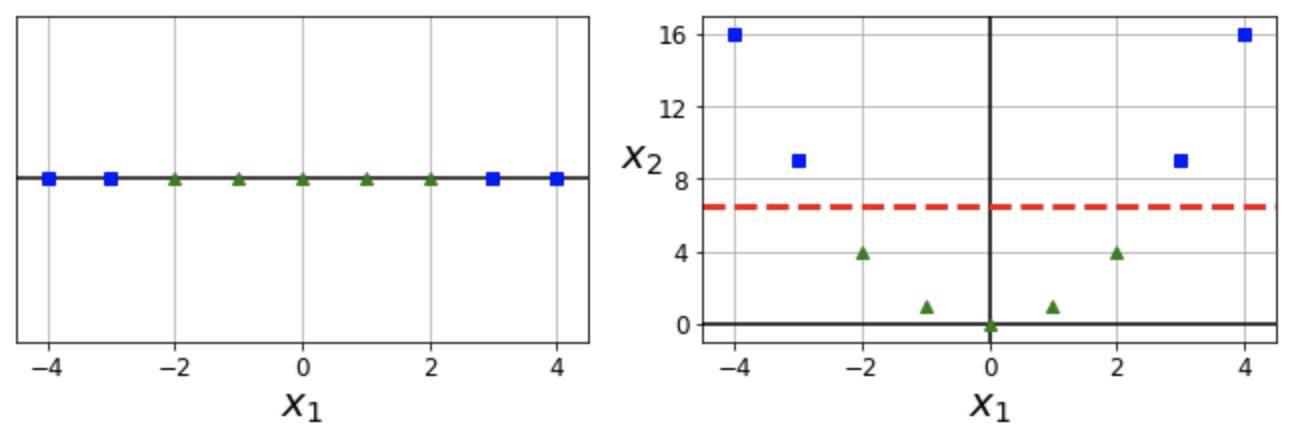
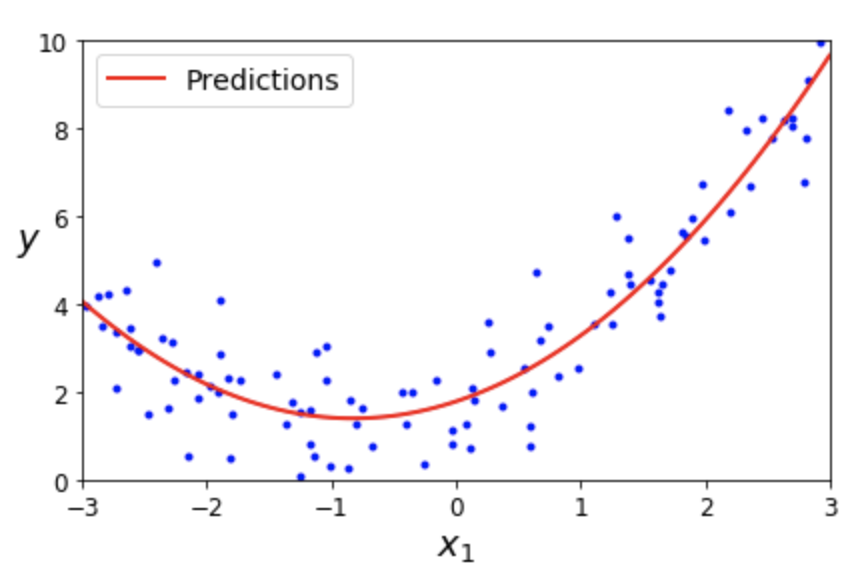
  • 다항 특성 + 선형 회귀(4장): 특성 $x_1$ 하나만 갖는 모델에 새로운 특성 $x_1^2$을 추가한 후 선형회귀 적용

    $$\hat y = \theta_0 + \theta_1\, x_1 + \theta_2\, x_1^{2}$$

  • 예제 2: moons 데이터셋. 마주보는 두 개의 반원 모양으로 두 개의 클래스로 구분되는 데이터
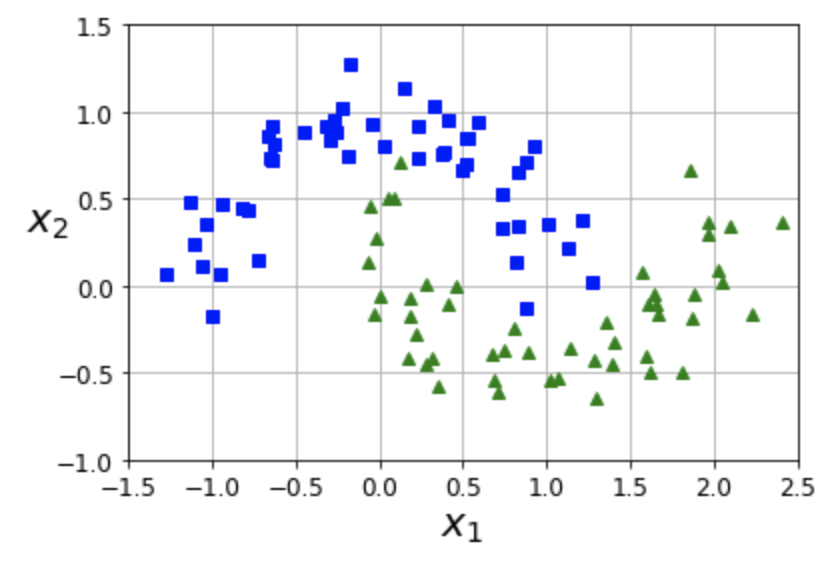
# 3차 항까지 추가
polynomial_svm_clf = Pipeline([
        ("poly_features", PolynomialFeatures(degree=3)),
        ("scaler", StandardScaler()),
        ("svm_clf", LinearSVC(C=10, loss="hinge", random_state=42))
    ])

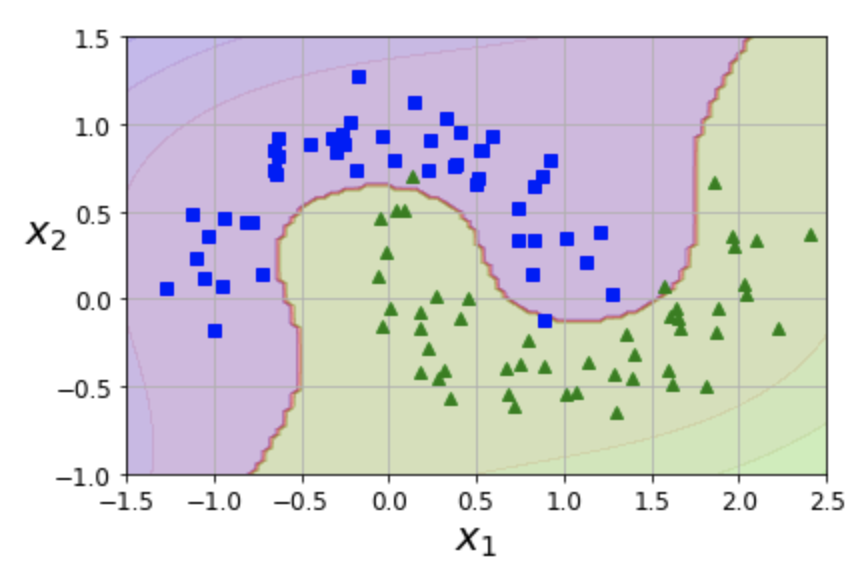
참고 영상: SVM + 다항 커널

  • 3차원의 선형 방정식 그래프 예제:
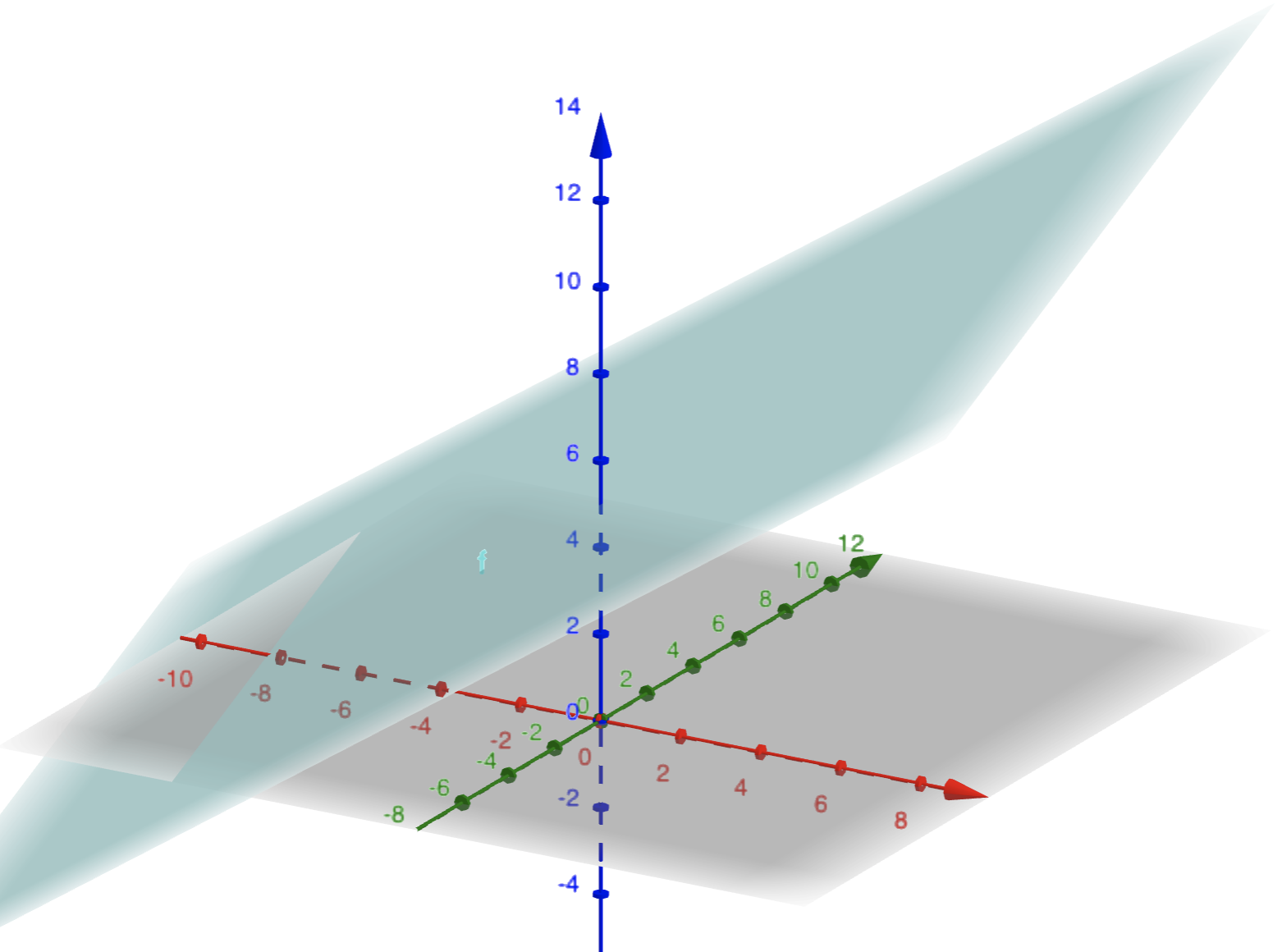
$$z = \frac{3}{5} x + \frac{1}{5}y + 5 \quad\Longleftrightarrow\quad 3x + y - 5z + 25 = 0$$

<그림 출처: 지오지브라(GeoGebra)>

SVC + 다항 커널¶

  • SVM 모델을 훈련시킬 때 다항 특성을 실제로는 추가 하지 않으면서 수학적으로는 추가한 효과를 내는 성질 이용

  • 예제: moons 데이터셋

    poly_kernel_svm_clf = Pipeline([
          ("scaler", StandardScaler()),
          ("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5)) ])
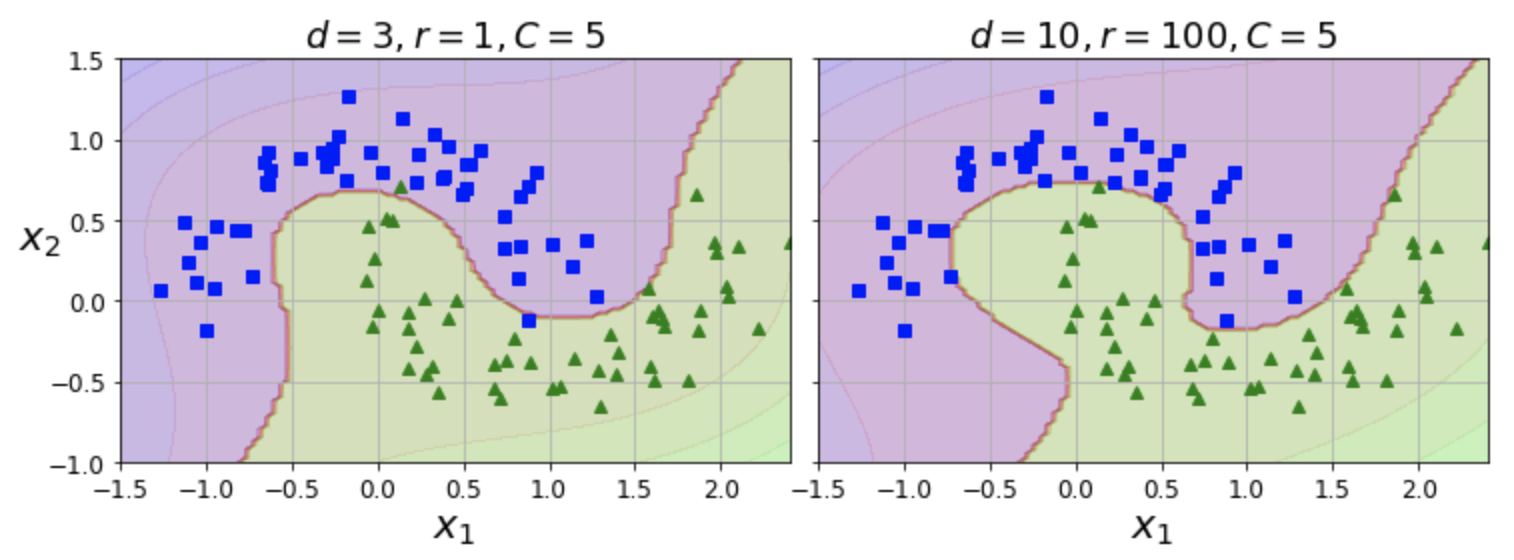
왼편 그래프 오른편 그래프
degree 3차 다항 커널 10차 다항 커널
coef0(r) 높은 차수 강조 조금 높은 차수 강조 많이

적절한 하이퍼파라미터 선택¶

  • 모델이 과대적합이면 차수를 줄여야 함
  • 적절한 하이퍼파라미터는 그리드 탐색 등을 이용하여 찾음
  • 처음에는 그리드의 폭을 크게, 그 다음에는 좀 더 세밀하게 검색
  • 하이퍼파라미터의 역할을 잘 알고 있어야 함

5.2.2 유사도 특성¶

유사도 함수¶

  • 유사도 함수: 랜드마크(landmark)라는 특정 샘플과 각 샘플 사이의 유사도(similarity)를 측정하는 함수

  • 유사도 함수 예제: 가우시안 방사 기저 함수(RBF, radial basis function)

    $$ \phi(\mathbf x, \ell) = \exp(-\gamma\, \lVert \mathbf x - \ell \lVert^2) $$

    • $\ell$: 랜드마크
    • $\gamma$: 랜드마크에서 멀어질 수록 0에 수렴하는 속도를 조절함
    • $\gamma$ 값이 클수록 가까운 샘플 선호, 즉 샘플들 사이의 영향을 보다 적게 고려하여 모델의 자유도를 높이게 되어 과대적합 위험 커짐.
  • 예제
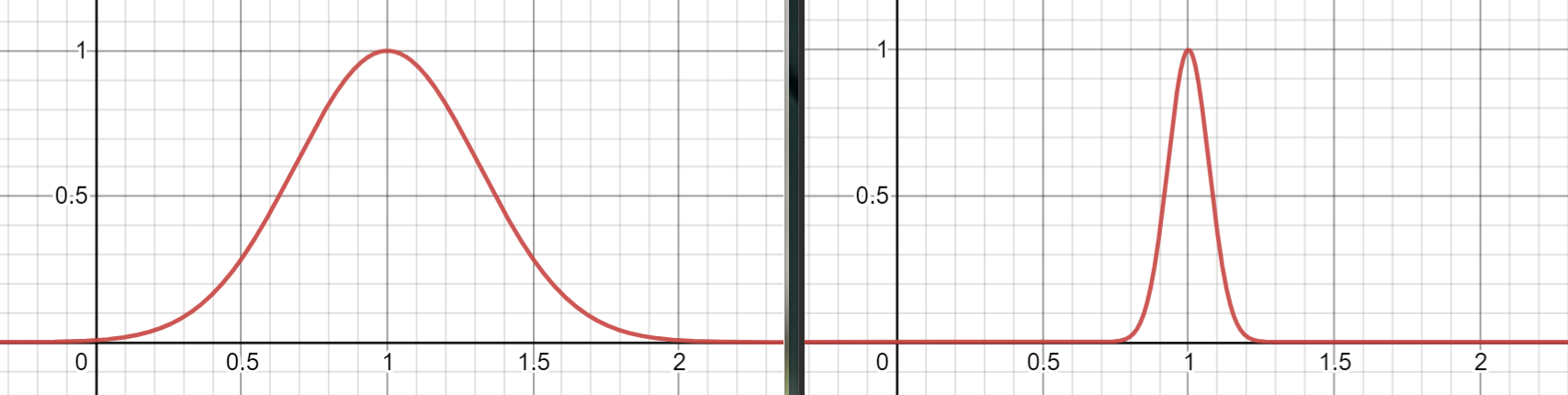
$$ \exp(-5\, \lVert \mathbf x - 1 \lVert^2) \qquad\qquad\qquad \exp(-100\, \lVert \mathbf x - 1 \lVert^2) $$

<그림 출처: 데스모스(desmos)>

유사도 특성 추가 + 선형 SVC¶

  • 모든 샘플을 랜드마크로 지정 후 각 랜드마크에 대한 유사도를 새로운 특성으로 추가하는 방식이 가장 간단함.
  • ($n$ 개의 특성을 가진 $m$ 개의 샘플) $\Rightarrow$ ($n + m$ 개의 특성을 가진 $m$ 개의 샘플)
  • 장점: 차원이 커지면서 선형적으로 구분될 가능성이 높아짐.
  • 단점: 훈련 세트가 매우 클 경우 동일한 크기의 아주 많은 특성이 생성됨.
  • 예제
    • 랜드마크: -2와 1
    • $x_2$와 $x_3$: 각각 -2와 1에 대한 가우시안 RBF 함수로 계산한 유사도 특성
    • 화살표가 가리키는 점: $\mathbf x = -1$

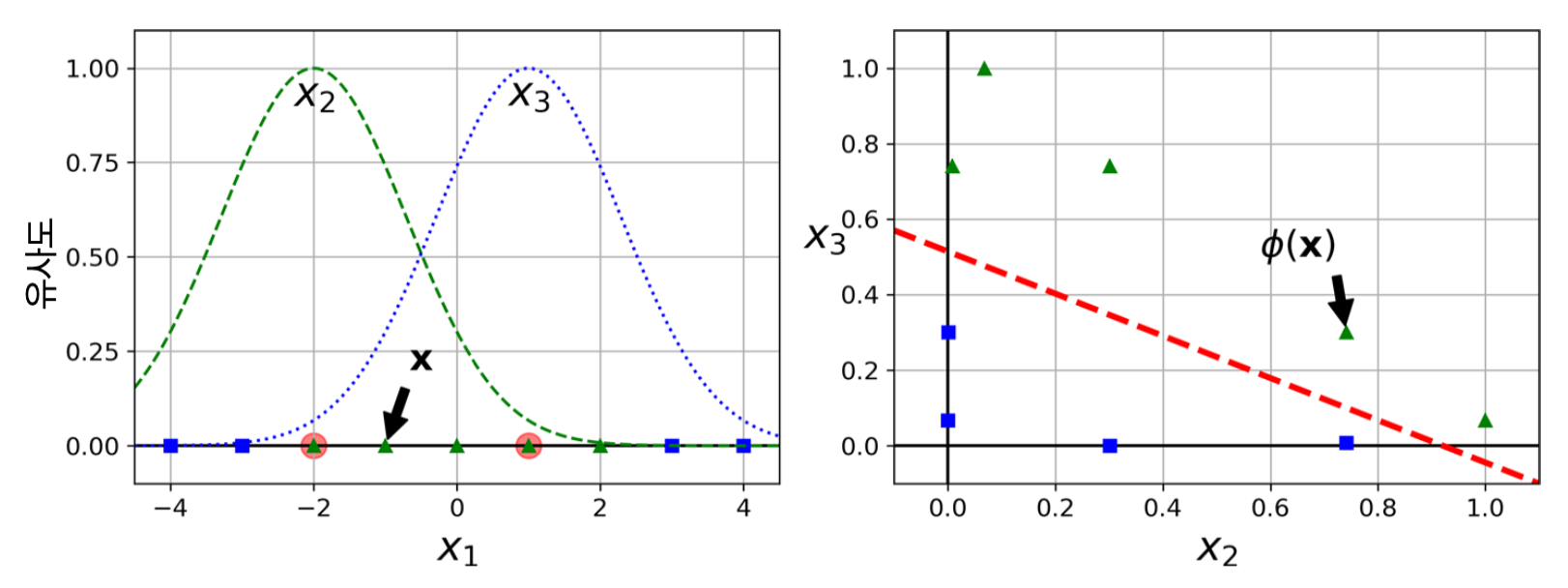
5.2.3 가우시안 RBF 커널¶

  • SVM 모델을 훈련시킬 때 유사도 특성을 실제로는 추가 하지 않으면서 수학적으로는 추가한 효과를 내는 성질 이용
rbf_kernel_svm_clf = Pipeline([
        ("scaler", StandardScaler()),
        ("svm_clf", SVC(kernel="rbf", gamma=0.1, C=0.001)) ])

SVC + RBF 커널 예제: moons 데이터셋¶

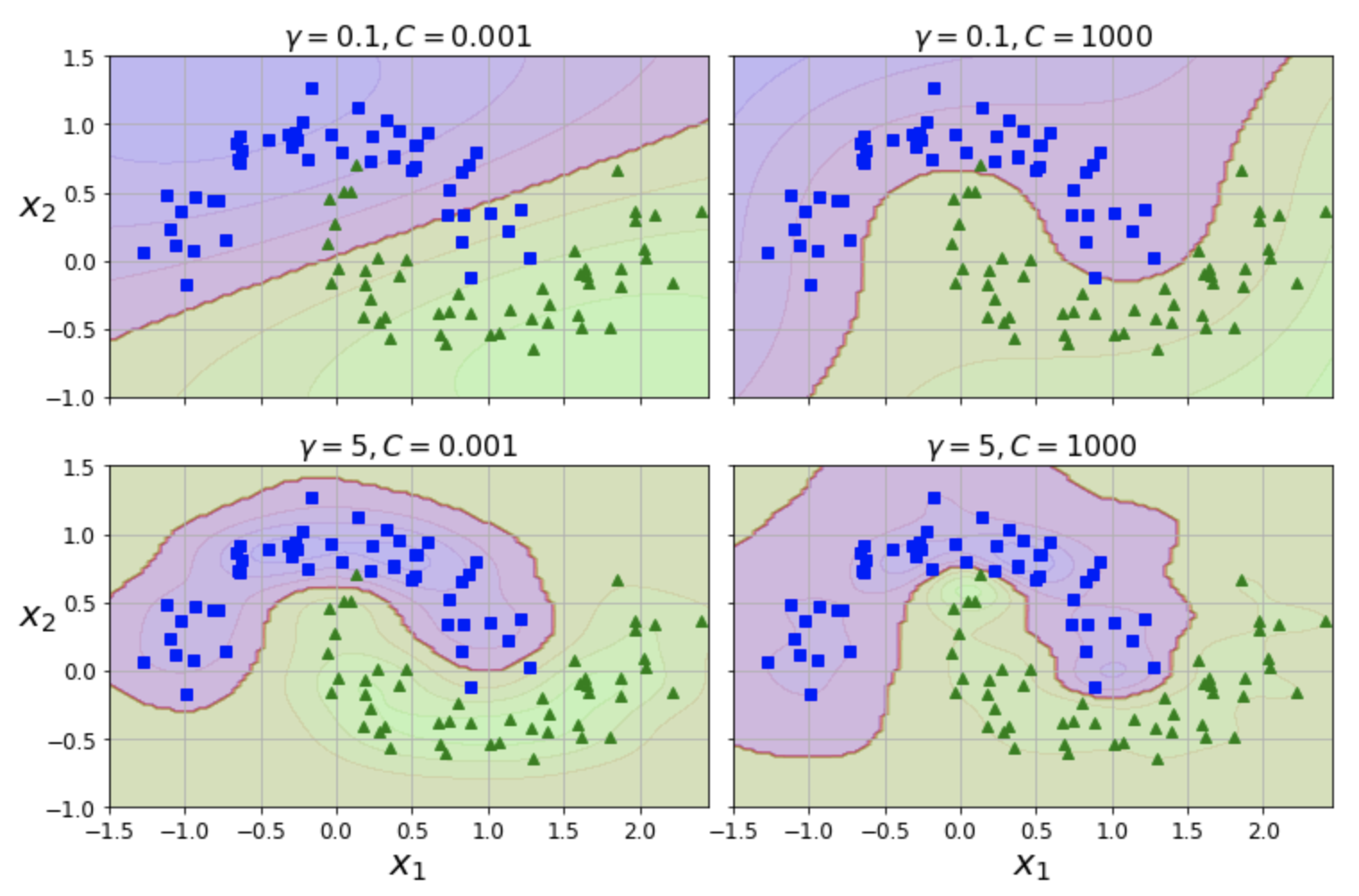
상단 그래프 하단 그래프
gamma 랜드마크에 조금 집중 랜드마크에 많이 집중
왼편 그래프                    오른편 그래프
C 규제 많이 규제 적게

추천 커널¶

  • SVC의 kernel 기본값은 "rbf" => 대부분의 경우 이 커널이 잘 맞음
  • 선형 모델이 예상되는 경우 SVC의 "linear" 커널을 사용할 수 있음 하지만 훈련 세트가 크거나 특성이 아주 많을 경우 LinearSVC가 빠름
  • 시간과 컴퓨팅 성능이 허락한다면 교차 검증, 그리드 탐색을 이용하여 적절한 커널을 찾아볼 수 있음
  • 훈련 세트에 특화된 커널이 알려져 있다면 해당 커널을 사용

5.2.4 계산 복잡도¶

분류기 시간 복잡도(m 샘플 수, n 특성 수) 외부 메모리 학습 스케일 조정 커널 트릭 다중 클래스 분류
LinearSVC $O(m \times n)$ 미지원 필요 미지원 OvR 기본
SGDClassifier $O(m \times n)$ 지원 필요 미지원 지원
SVC $O(m^2 \times n) \sim O(m^3 \times n)$ 미지원 필요 지원 OvR 기본