4장 모델 훈련 2부¶

감사의 글¶

자료를 공개한 저자 오렐리앙 제롱과 강의자료를 지원한 한빛아카데미에게 진심어린 감사를 전합니다.

4.5 규제를 사용하는 선형 모델¶

자유도와 규제¶

  • 자유도(degree of freedom): 학습 모델 결정에 영향을 주는 요소(특성)들의 수
    • 단순 선형 회귀의 경우: 특성 수
    • 다항 선형 회귀 경우: 차수
  • 규제(regularization): 자유도 제한
    • 단순 선형 회귀 모델에 대한 규제: 가중치 역할 제한
    • 다항 선형 회귀 모델에 대한 규제: 차수 줄이기

가중치를 규제하는 선형 회귀 모델¶

  • 릿지 회귀
  • 라쏘 회귀
  • 엘라스틱넷

규제 적용 주의사항¶

규제항은 훈련 과정에만 사용된다. 테스트 과정에는 다른 기준으로 성능을 평가한다.

  • 훈련 과정: 비용 최소화 목표
  • 테스트 과정: 최종 목표에 따른 성능 평가
    • 예제: 분류기의 경우 재현율/정밀도 기준으로 성능 평가

4.5.1 릿지 회귀¶

  • 비용함수
$$J(\theta) = \textrm{MSE}(\theta) + \alpha \, \frac{1}{2} \sum_{i=1}^{n}\theta_i^2$$
  • $\alpha$(알파): 규제 강도 지정. $\alpha=0$이면 규제가 전혀 없는 기본 선형 회귀
  • $\alpha$가 커질 수록 가중치의 역할이 줄어듦. 비용을 줄이기 위해 가중치를 작게 유지하는 방향으로 학습
  • $\theta_0$은 규제하지 않음
  • 주의사항: 특성 스케일링 전처리를 해야 성능이 좋아짐.

4.5.2 라쏘 회귀¶

  • 비용함수
$$J(\theta) = \textrm{MSE}(\theta) + \alpha \, \sum_{i=1}^{n}\mid\theta_i\mid$$
  • $\alpha$(알파): 규제 강도 지정. $\alpha=0$이면 규제가 전혀 없는 기본 선형 회귀
  • $\theta_i$: 덜 중요한 특성을 무시하기 위해 $\mid\theta_i\mid$가 0에 수렴하도록 학습 유도.
  • $\theta_0$은 규제하지 않음

라쏘 회귀 대 릿지 회귀 비교¶

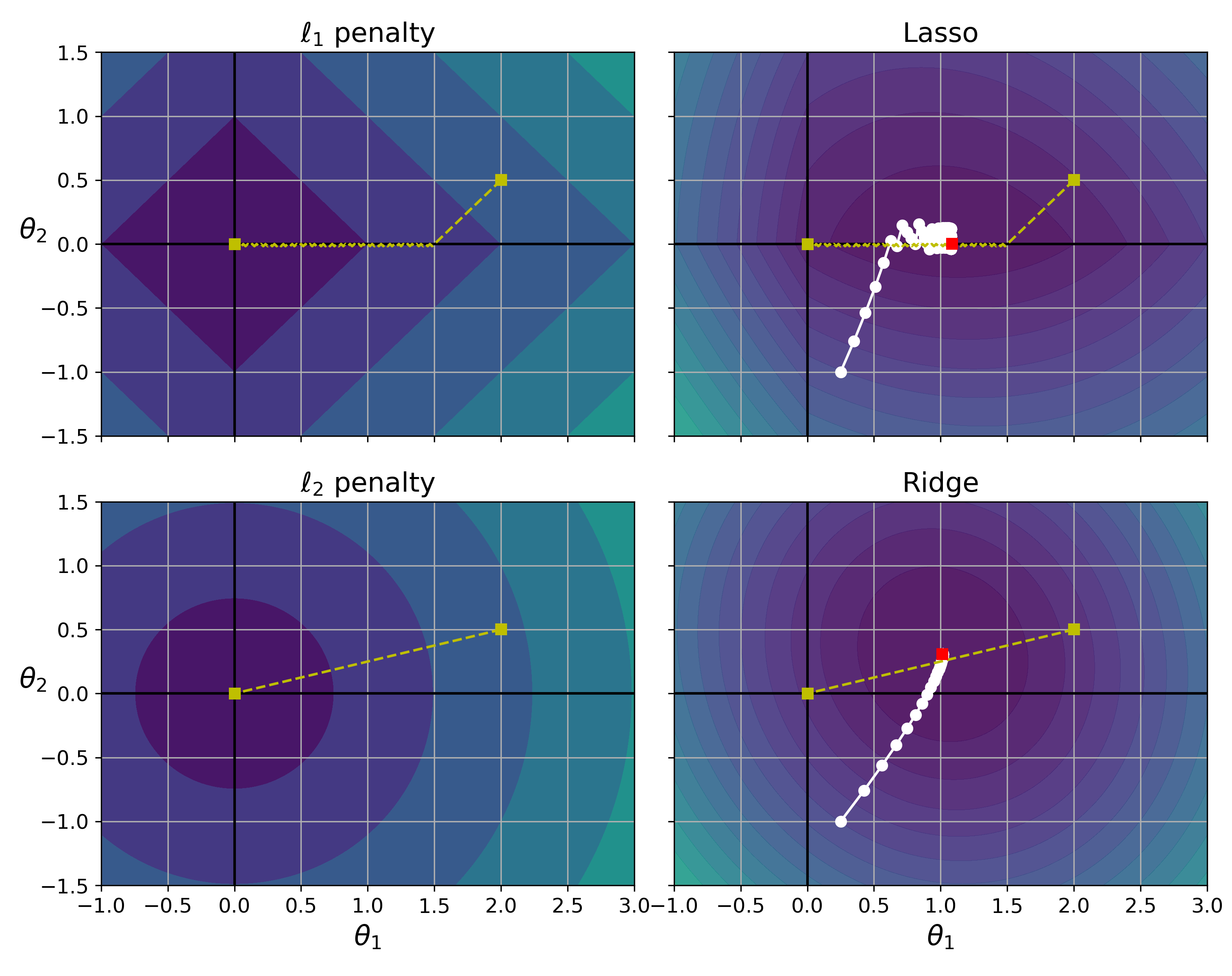
4.5.3 엘라스틱넷¶

  • 비용함수
$$J(\theta) = \textrm{MSE}(\theta) + r\, \alpha \, \sum_{i=1}^{n}\mid\theta_i\mid + \,\frac{1-r}{2}\, \alpha\, \sum_{i=1}^{n}\theta_i^2$$
  • 릿지 회귀와 라쏘 회귀를 절충한 모델
  • 혼합 비율 $r$을 이용하여 릿지 규제와 라쏘 규제를 적절하게 조절

규제 사용 방법¶

  • 대부분의 경우 약간이라도 규제 사용 추천
  • 릿지 규제가 기본
  • 유용한 속성이 많지 않다고 판단되는 경우
    • 라쏘 규제나 엘라스틱넷 활용 추천
    • 불필요한 속성의 가중치를 0으로 만들기 때문
  • 특성 수가 훈련 샘플 수보다 크거나 특성 몇 개가 강하게 연관되어 있는 경우
    • 라쏘 규제는 적절치 않음.
    • 엘라스틱넷 추천

4.5.4 조기 종료¶

  • 모델의 훈련 세트에 대한 과대 적합 방지를 위해 훈련을 적절한 시기에 중단시키기.
  • 조기 종료: 검증 데이터에 대한 손실이 줄어 들다가 다시 커지는 순간 훈련 종료
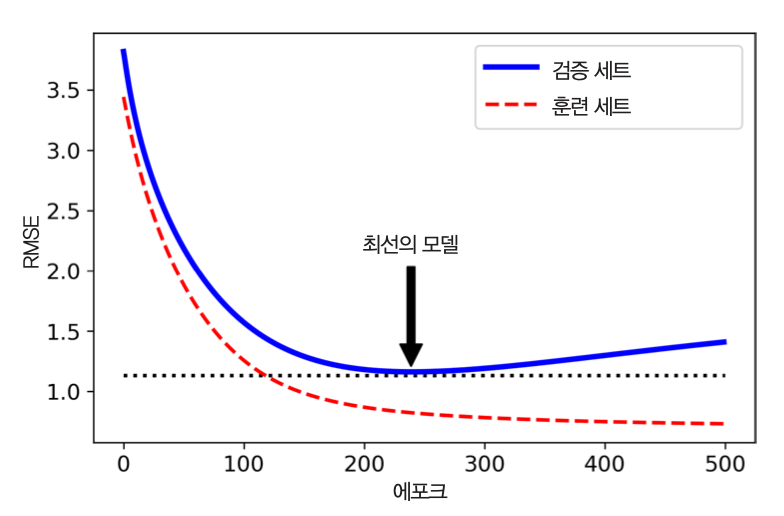
  • 확률적 경사 하강법 등의 경우 손실 곡선의 진동 발생. 검증 손실이 한동안 최솟값보다 높게 유지될 때 훈련 멈춤. 최소 검증 손실 모델 확인.

4.6 로지스틱 회귀¶

회귀 모델을 분류 모델로 활용할 수 있다.

  • 이진 분류: 로지스틱 회귀
  • 다중 클래스 분류: 소프트맥스 회귀

4.6.1 확률 추정¶

  • 시그모이드 함수
$$\sigma(t) = \frac{1}{1 + e^{-t}}$$
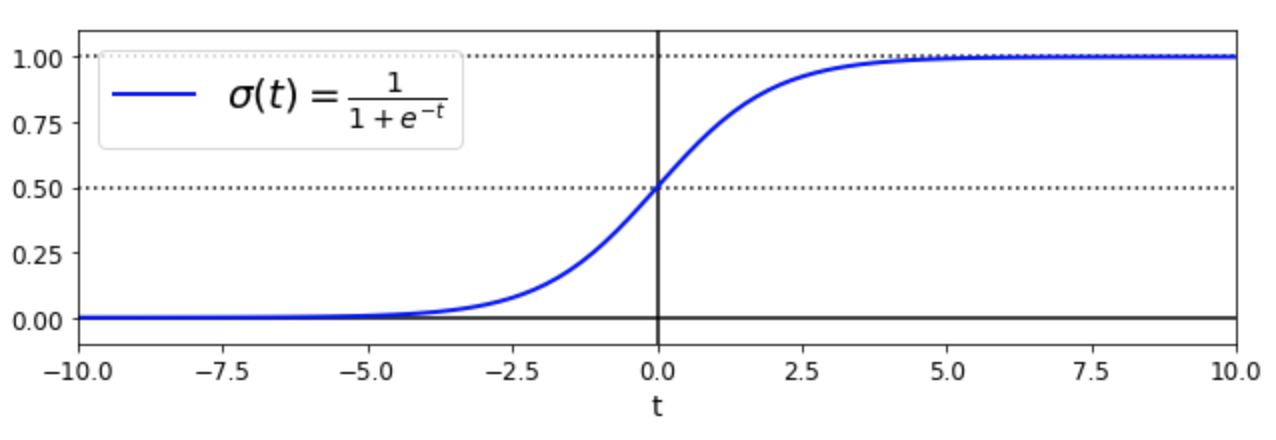
  • 로지스틱 회귀 모델에서 샘플 $\mathbf x$가 양성 클래스에 속할 확률
$$\hat p = h_\theta (\mathbf x) = \sigma(\theta_0 + \theta_1\, x_1 + \cdots + \theta_n\, x_n)$$

예측값¶

$$ \hat y = \begin{cases} 0 & \text{if}\,\, \hat p < 0.5 \\ 1 & \text{if}\,\, \hat p \ge 0.5 \end{cases} $$
  • 양성 클래스인 경우:
$$\theta_0 + \theta_1\, x_1 + \cdots + \theta_n\, x_n \ge 0$$
  • 음성 클래스인 경우:
$$\theta_0 + \theta_1\, x_1 + \cdots + \theta_n\, x_n < 0$$

4.6.2 훈련과 비용함수¶

  • 비용함수: 로그 손실(log loss) 함수 사용
$$ J(\theta) = - \frac{1}{m}\, \sum_{i=1}^{m}\, [y^{(i)}\, \log(\,\hat p^{(i)}\,) + (1-y^{(i)})\, \log(\,1 - \hat p^{(i)}\,)] $$
  • 모델 훈련: 위 비용함수에 대해 경사 하강법 적용

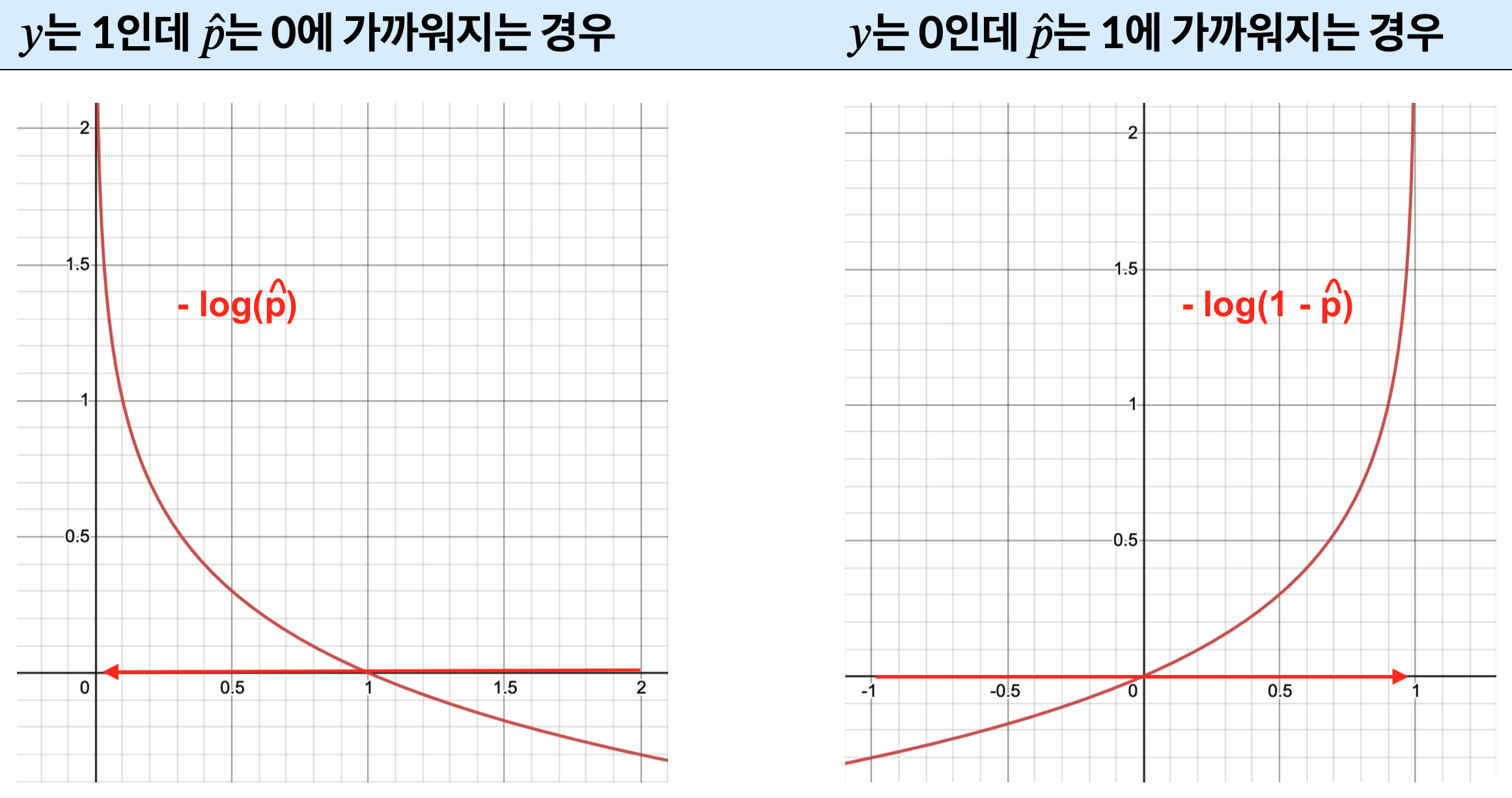
로그 손실 함수 이해¶

  • 틀린 예측을 하면 손실값이 많이 커짐
$$ - [y\, \log(\,\hat p\,) + (1-y)\, \log(\,1 - \hat p\,)] $$

로그 손실 함수의 편도 함수¶

$$ \dfrac{\partial}{\partial \theta_j} \text{J}(\boldsymbol{\theta}) = \dfrac{1}{m}\sum\limits_{i=1}^{m}\left(\mathbf{\sigma(\boldsymbol{\theta}}^T \mathbf{x}^{(i)}) - y^{(i)}\right)\, x_j^{(i)} $$
  • 편도 함수가 선형 회귀의 경우와 매우 비슷한 것에 대한 확률론적 근거가 있음.
  • 참고: 앤드류 응(Andrew Ng) 교수의 Stanford CS229

4.6.3 결정 경계¶

예제: 붓꽃 데이터셋¶

  • 꽃받침(sepal)과 꽃입(petal)과 관련된 4개의 특성 사용
    • 꽃받침 길이
    • 꽃받침 너비
    • 꽃잎 길이
    • 꽃잎 너비
  • 타깃: 세 개의 품종
    • 0: Iris-Setosa(세토사)
    • 1: Iris-Versicolor(버시컬러)
    • 2: Iris-Virginica(버지니카)

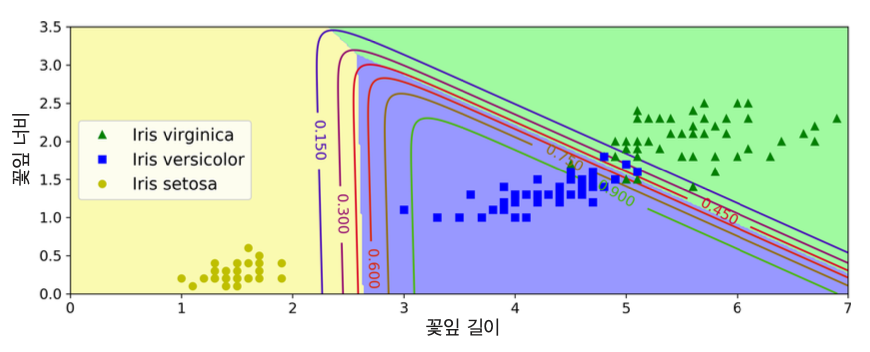
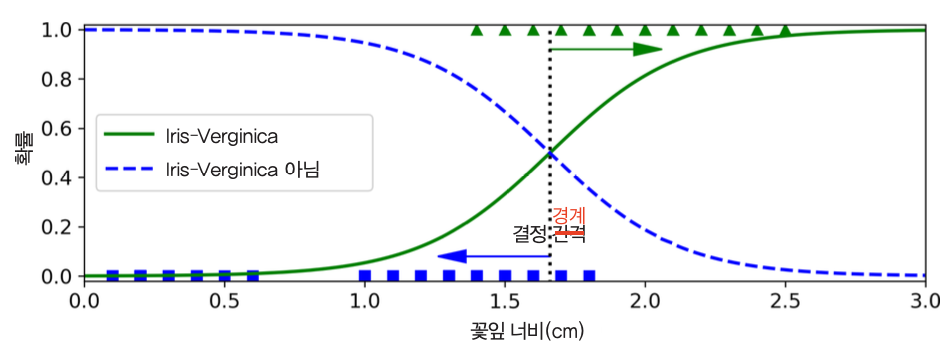
꽃잎의 너비를 기준으로 Iris-Virginica 여부 판정하기¶

  • 결정경계: 약 1.6cm

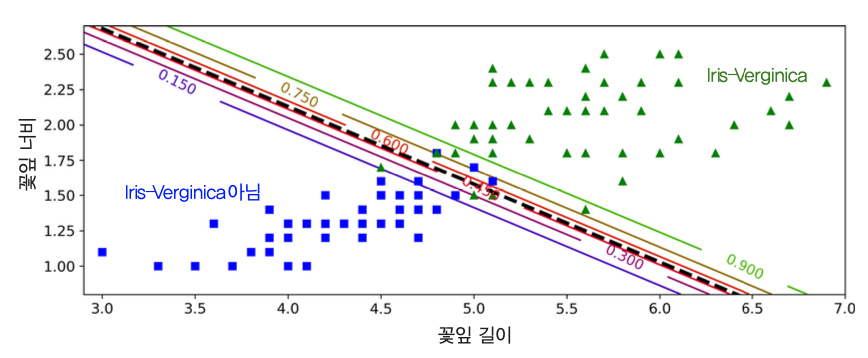
꽃잎의 너비와 길이를 기준으로 Iris-Virginica 여부 판정하기¶

  • 결정경계: 검정 점선

로지스틱 회귀 규제하기¶

  • 하이퍼파라미터 penalty와 C 이용
  • penalty
    • l1, l2, elasticnet 세 개중에 하나 사용.
    • 기본은 l2, 즉, $\ell_2$ 규제를 사용하는 릿지 규제.
    • elasticnet을 선택한 경우 l1_ration 옵션 값을 함께 지정.
  • C
    • 릿지 또는 라쏘 규제 정도를 지정하는 $\alpha$의 역수에 해당.
    • 따라서 0에 가까울 수록 강한 규제 의미.

4.6.4 소프트맥스(softmax) 회귀¶

  • 로지스틱 회귀 모델을 일반화하여 다중 클래스 분류를 지원하도록 한 회귀 모델
  • 다항 로지스틱 회귀 라고도 불림
  • 주의사항: 소프트맥스 회귀는 다중 출력 분류 지원 못함. 예를 들어, 하나의 사진에서 여러 사람의 얼굴 인식 불가능.

소프트맥스 회귀 학습 아이디어¶

  • 샘플 $\mathbf x$가 주어졌을 때 각각의 분류 클래스 $k$ 에 대한 점수 $s_k(\mathbf x)$ 계산. 즉, k*(n+1) 개의 파라미터를 학습시켜야 함.
$$ s_k(\mathbf x) = \theta_0^{(k)} + \theta_1^{(k)}\, x_1 + \cdots + \theta_n^{(k)}\, x_n $$

  • 소프트맥스 함수를 이용하여 각 클래스 $k$에 속할 확률 $\hat p_k$ 계산
$$ \hat p_k = \frac{\exp(s_k(\mathbf x))}{\sum_{j=1}^{K}\exp(s_j(\mathbf x))} $$
  • 추정 확률이 가장 높은 클래스 선택
$$ \hat y = \mathrm{argmax}_k s_k(\mathbf x) $$

소프트맥스 회귀 비용함수¶

  • 각 분류 클래스 $k$에 대한 적절한 가중치 벡터 $\theta_k$를 학습해 나가야 함.
  • 비용함수: 크로스 엔트로피 비용 함수 사용
$$ J(\Theta) = - \frac{1}{m}\, \sum_{i=1}^{m}\sum_{k=1}^{K} y^{(i)}_k\, \log(\hat{p}_k^{(i)}) $$
  • 위 비용함수에 대해 경사 하강법 적용
  • $K=2$이면 로지스틱 회귀의 로그 손실 함수와 정확하게 일치.
  • 주어진 샘플의 타깃 클래스를 제대로 예측할 경우 높은 확률값 계산
  • 크로스 엔트로피 개념은 정보 이론에서 유래함. 자세한 설명은 생략.

다중 클래스 분류 예제¶

  • 사이킷런의 LogisticRegression 예측기 활용
    • multi_class=multinomial로 지정
    • solver=lbfgs: 다중 클래스 분류 사용할 때 반드시 지정
  • 붓꽃 꽃잎의 너비와 길이를 기준으로 품종 분류
    • 결정경계: 배경색으로 구분
    • 곡선: Iris-Versicolor 클래스에 속할 확률