4장 모델 훈련 1부

감사의 글

자료를 공개한 저자 오렐리앙 제롱과 강의자료를 지원한 한빛아카데미에게 진심어린 감사를 전합니다.

1부 주요 내용

• 수학적으로 선형 회귀 모델 구하기

• 경사하강법으로 선형 회귀 모델 구하기

• 경사하강법 종류
  • 배치 경사하강법
  • 미니배치 경사하강법
  • 확률적 경사하강법(SGD)

• 다항 회귀: 비선형 모델 훈련법

• 학습 곡선: 과소, 과대 적합 감지

2부 주요 내용

• 규제 선형 모델
  • 과대적합 위험 감소시키기

• 로지스틱 회귀와 소프트맥스 회귀
  • 회귀 모델을 분류기로 활용하기

4.1 선형 회귀

선형 회귀 모델 함수

• 한 개의 특성 $x_1$을 사용하는 $i$ 번째 훈련 샘플에 대한 예측값

$$\hat y^{(i)} = \theta_0 + \theta_1\, x_1^{(i)}$$

• $n\ge 1$ 개의 특성을 사용하는 $i$번째 훈련 샘플에 대한 예측값

  • 예제: 캘리포니아 주택 가격 예측 모델

    $$\hat y^{(i)} = \theta_0 + \theta_1\, x_1^{(i)} + \cdots + \theta_{16}\, x_{16}^{(i)}$$

  • $\hat y^{(i)}$: $i$ 번째 훈련 샘플에 대한 예측값
  • $x_k^{(i)}$: $i$ 번째 훈련 샘플의 $k$ 번째 특성값
  • $\theta_k$: 편향($\theta_0$) 및 $k$ 번째 특성에 대한 가중치 파라미터

예측 함수

$$ \begin{align*} \hat y^{(i)} & = \theta_0 + \theta_1\, x_1^{(i)} + \cdots + \theta_n\, x_n^{(i)}\\ & = \theta^T\, \mathbf{x}^{(i)} \\ & = h_\theta (\mathbf{x}^{(i)}) \end{align*} $$

• $\mathbf{x}^{(i)} = [1, x_1^{(i)}, \dots, x_n^{(i)}]^T$.
  • $n$은 특성 개수
  • 1이 추가됨에 주의할 것.
• $\theta = [\theta_0, \theta_1, \dots, \theta_n]^T$
• $h_\theta(\cdot)$: 예측 함수, 즉 모델의 predict() 메서드를 가리킴.

선형 회귀 모델의 행렬 연산 표기법

• $\mathbf{X}$: 전체 훈련 세트, 즉 모든 훈련 샘플을 모아놓은 행렬.
  • $m$은 훈련 세트의 크기.
  • $\mathbf{X}$는 $(m, n+1)$ 모양의 행렬

$$ \mathbf{X}= \begin{bmatrix} (\mathbf{x}^{(1)})^T \\ \vdots \\ (x_n^{(m)})^T \end{bmatrix} $$

• 넘파이 2차원 어레이 표현

데이터	어레이 기호	어레이 모양(shape)
레이블, 예측값	$\mathbf y$, $\hat{\mathbf y}$	$(m, 1)$
가중치	$\theta$	$(n+1, 1)$
훈련 세트	$\mathbf X$	$(m, n+1)$

비용함수: 평균 제곱 오차(MSE)

• MSE를 활용한 선형 회귀 모델 성능 평가

$$ \mathrm{MSE}(\theta) := \mathrm{MSE}(\mathbf X, h_\theta) = \frac 1 m \sum_{i=1}^{m} \big(\theta^{T}\, \mathbf{x^{(i)}} - y^{(i)}\big)^2 $$

• 목표: $\mathrm{MSE}(\theta)$가 최소가 되도록 하는 $\theta$ 찾기

• 참고: $m, \mathbf{x}^{(i)}, y^{(i)}$은 모두 주어졌음.

• 방식 1: 정규방정식 또는 특이값 분해(SVD) 활용
  • 드물지만 수학적으로 비용함수를 최소화하는 $\theta$ 값을 직접 계산할 수 있는 경우 활용
  • 계산복잡도가 $O(n^2)$ 이상인 행렬 연산을 수행해야 함.
  • 따라서 특성 수($n$)이 큰 경우 메모리 관리 및 시간복잡도 문제때문에 비효율적임.

• 방식 2: 경사하강법
  • 특성 수가 매우 크거나 훈련 샘플이 너무 많아 메모리에 한꺼번에 담을 수 없을 때 적합
  • 일반적으로 선형 회귀 모델 훈련에 적용되는 기법

4.1.1 정규 방정식

정규 방정식을 이용하여 비용함수를 최소화 하는 $\theta$를 아래와 같이 구할 수 있음:

$$ \hat \theta = (\mathbf{X}^T\, \mathbf{X})^{-1}\, \mathbf{X}^T\, \mathbf{y} $$

SVD(특잇값 분해) 활용

• 행렬 연산과 역행렬 계산은 계산 복잡도가 $O(n^{2.4})$ 이상이고 항상 역행렬 계산이 가능한 것도 아님.

• 반면에, 특잇값 분해를 활용하여 얻어지는 무어-펜로즈(Moore-Penrose) 유사 역행렬 $\mathbf{X}^+$ 계산이 보다 효율적임. 계산 복잡도는 $O(n^2)$.

$$ \hat \theta = \mathbf{X}^+\, \mathbf{y} $$

4.2 경사 하강법

기본 아이디어

• 훈련 세트를 이용한 훈련 과정 중에 가중치 등과 같은 파라미터를 조금씩 반복적으로 조정하기

• 조정 기준: 비용 함수의 크기 줄이기

경사 하강법 관련 주요 개념

최적 학습 모델

• 비용함수를 최소화하는 또는 효용함수를 최대화하는 파라미터를 사용하는 모델

파라미터

• 예측값을 생성하는 함수로 구현되는 학습 모델에 사용되는 파라미터
• 예제: 선형 회귀 모델에 사용되는 편향과 가중치 파라미터

$$\theta = \theta_0,\theta_1, \dots, \theta_n$$

비용함수

• 모델이 얼마나 나쁜지를 계산해주는 함수
• 예제: 선형 회귀 모델의 평균 제곱 오차(MSE)

$$ \mathrm{MSE}(\theta) = \frac 1 m \sum_{i=1}^{m} \big(\theta^{T}\, \mathbf{x^{(i)}} - y^{(i)}\big)^2 $$

전역 최솟값

• 비용함수가 가질 수 있는 최솟값
• 예제: 선형 회귀 모델의 평균 제곱 오차(MSE) 함수가 갖는 최솟값

그레이디언트 벡터

• 다변수 함수의 미분값.

• (그레이디언트) 벡터는 방향과 크기에 대한 정보 제공

• 그레이디언트가 가리키는 방향의 반대 방향으로 움직여야 가장 빠르게 전역 최솟값에 접근

• 예제: 선형 회귀 MSE의 그레이디언트 벡터 $\nabla_\theta \textrm{MSE}(\theta)$

$$ \nabla_\theta \textrm{MSE}(\theta) = \begin{bmatrix} \frac{\partial}{\partial \theta_0} \textrm{MSE}(\theta) \\ \frac{\partial}{\partial \theta_1} \textrm{MSE}(\theta) \\ \vdots \\ \frac{\partial}{\partial \theta_n} \textrm{MSE}(\theta) \end{bmatrix} = \frac{2}{m}\, \mathbf{X}^T\, (\mathbf{X}\, \theta^T - \mathbf y) $$

학습률

• 훈련 과정에서의 비용함수 파라미터 조정 비율

예제: 선형회귀 모델 파라미터 조정 과정

• $\theta$를 임의의 값으로 지정한 후 훈련 시작

• 아래 단계를 $\theta$가 특정 값에 지정된 오차범위 내로 수렴할 때까지 반복
  1. (배치 크기로) 지정된 수의 훈련 샘플을 이용하여 학습.
  2. 학습 후 $\mathrm{MSE}(\theta)$ 계산.
  3. 이전 $\theta$에서 $\nabla_\theta \textrm{MSE}(\theta)$과 학습률 $\eta$를 곱한 값 빼기.

$$\theta^{(\text{new})} = \theta^{(\text{old})}\, -\, \eta\cdot \nabla_\theta \textrm{MSE}(\theta^{(\text{old})})$$

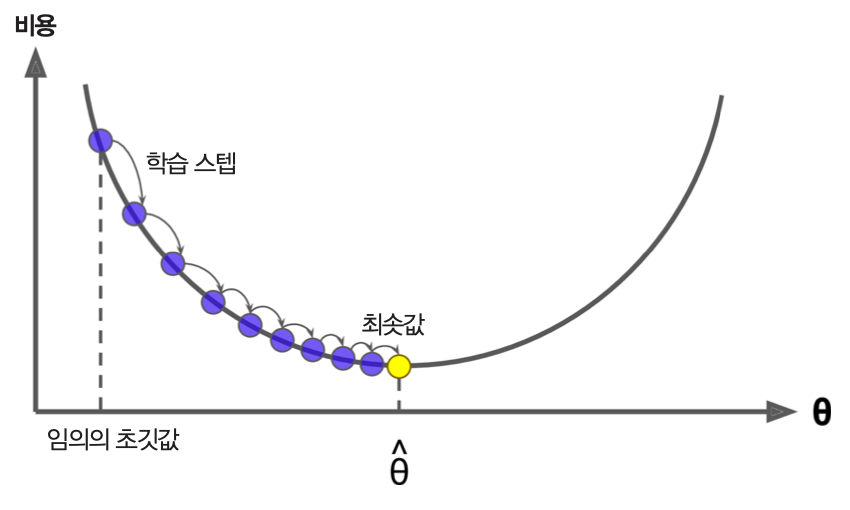
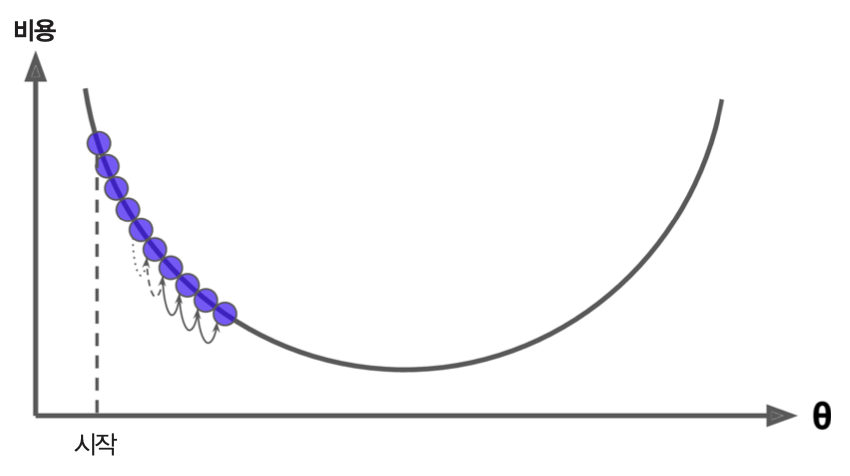
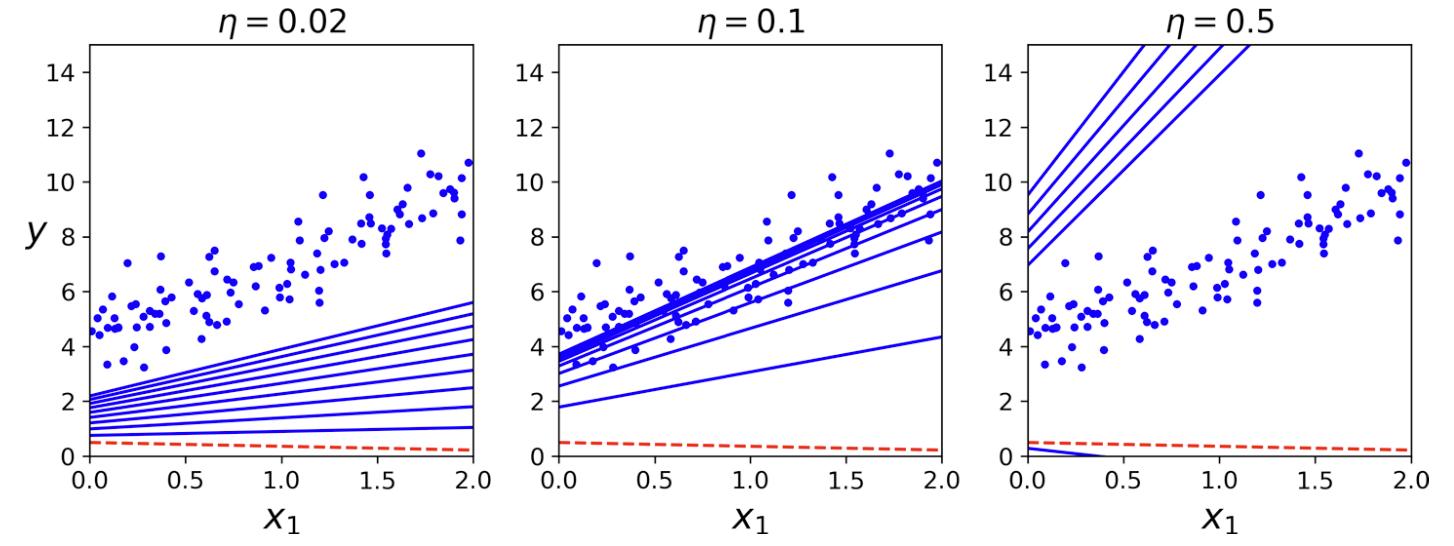
• 학습률이 너무 작은 경우: 비용 함수가 전역 최소값에 너무 느리게 수렴.

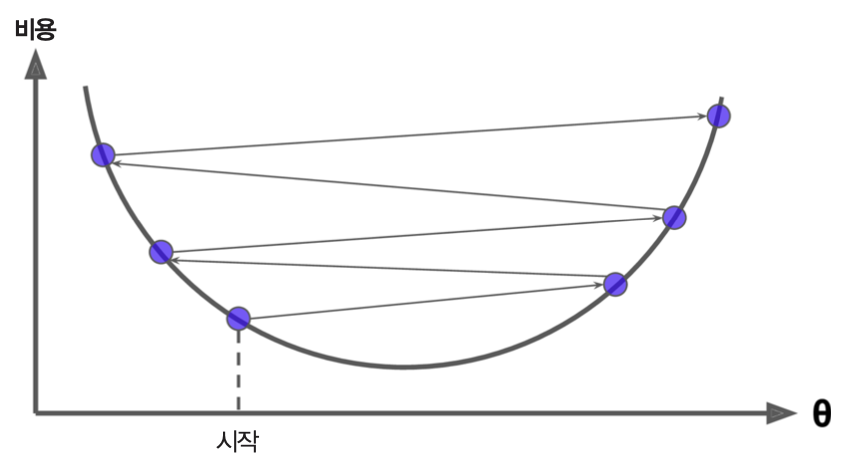
• 학습률이 너무 큰 경우: 비용 함수가 수렴하지 않음.

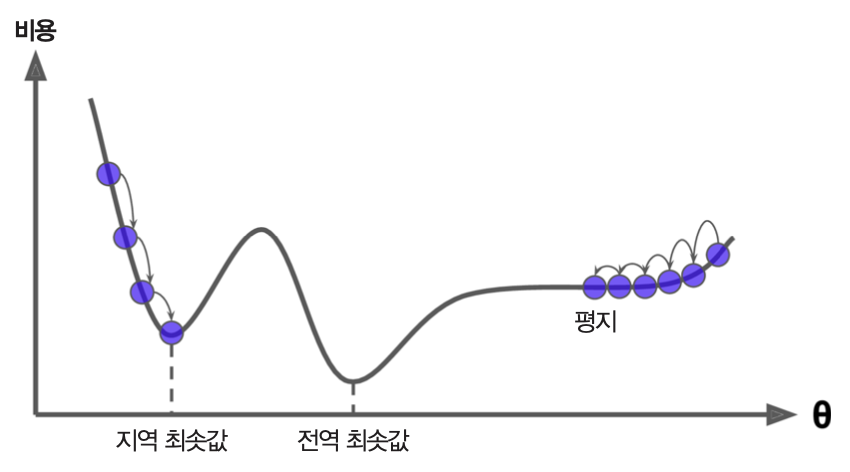
• (선형 회귀가 아닌 경우에) 시작점에 따라 지역 최솟값에 수렴하지 못할 수도 있음.

• 선형 회귀와 학습률

  • 비용함수(MSE)가 볼록 함수. 즉, 지역 최솟값을 갖지 않음
  • 따라서 학습률이 너무 크지 않으면 언젠가는 전역 최솟값에 수렴

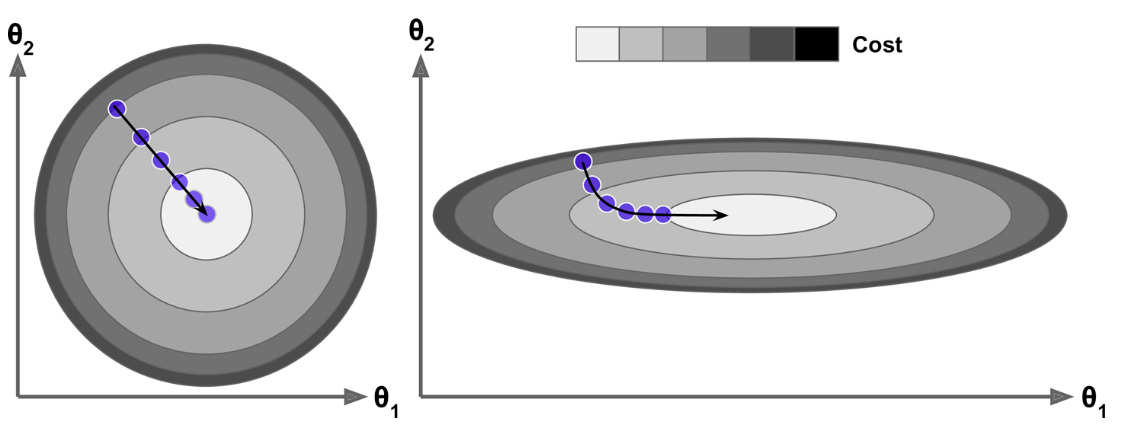
특성 스케일링

• 특성들의 스켈일을 통일시키면 보다 빠른 학습 이루어짐.

하이퍼파라미터(hyperparameter)

• 학습 모델을 지정할 때 사용되는 값. 학습률, 배치 크기, 에포크, 허용오차, 스텝 크기 등

• 에포크(epoch): 훈련 세트 크기만큼의 샘플을 훈련하는 단계
  • 에포크 수: 에포크 반복 횟수

• 배치(batch) 크기: 파라미터를 업데이트하기 위해, 즉 그레이디언트 벡터를 계산하기 위해 사용되는 훈련 샘플 수.

• 허용오차(tolerance): 비용함수의 그레이디언트 벡터의 크기가 허용오차보다 작아지면 학습 종료

• 스텝(step): 지정된 배치 크기의 샘플을 학습한 후에 파라미터를 조정하는 단계
  • 스텝 크기 = (훈련 샘플 수) / (배치 크기)
  • 예제: 훈련 세트의 크기가 1,000이고 배치 크기가 10이면, 하나의 에포크 기간동안 총 100번의 스텝이 실행됨.

경사 하강법 종류

배치 경사 하강법

• 전체 훈련 샘플을 대상으로 훈련한 후에, 즉 에포크마다 그레이디언트를 계산하여 파라미터 조정
• 주의: 여기서 사용되는 '배치'의 의미가 '배치 크기'의 '배치'와 다른 의미

확률적 경사 하강법

• 배치 크기: 1
• 즉, 하나의 훈련 샘플을 학습할 때마다 그레이디언트를 계산해서 파라미터 조정

미니배치 경사 하강법

• 배치 크기: 2에서 수백 사이
• 최적 배치 크기: 경우에 따라 다름. 여러 논문이 32 이하 추천

4.2.1 배치 경사 하강법

• 에포크와 허용오차

  • 에포크 수는 크게 설정한 후 허용오차를 지정하여 학습 시간 제한 필요. 이유는 포물선의 최솟점에 가까워질 수록 그레이디언트 벡터의 크기가 0에 수렴하기 때문임.

  • 허용오차와 에포크 수는 서로 반비례의 관계임. 즉, 오차를 1/10로 줄이려면 에포크 수를 10배 늘려야함.

• 단점

  • 훈련 세트가 크면 그레이디언트를 계산하는 데에 많은 시간 필요
  • 아주 많은 데이터를 저장해야 하는 메모리 문제도 발생 가능

• 주의사항

  • 사이킷런은 배치 경사 하강법을 활용한 선형 회귀 지원하지 않음. (책 176쪽, 표 4-1에서 사이킷런의 SGDRegressor가 배치 경사 하강법을 지원한다고 잘못 명시됨.)

학습율과 경사 하강법의 관계

4.2.2 확률적 경사 하강법

• 장점

  • 매우 큰 훈련 세트를 다룰 수 있음. 예를 들어, 외부 메모리(out-of-core) 학습을 활용할 수 있음
  • 학습 과정이 매우 빠르며 파라미터 조정이 불안정 할 수 있기 때문에 지역 최솟값에 상대적으로 덜 민감

• 단점: 학습 과정에서 파라미터의 동요가 심해서 경우에 따라 전역 최솟값에 수렴하지 못하고 계속해서 발산할 가능성도 높음

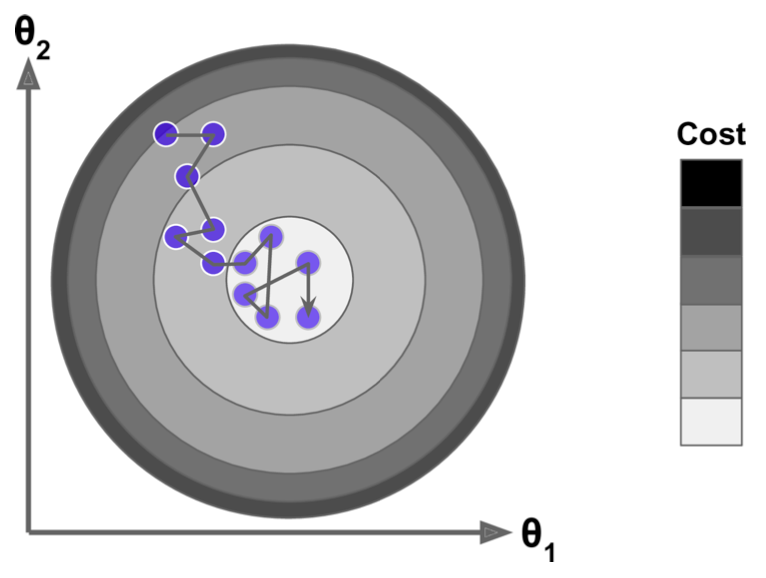
처음 20 단계 동안의 SGD 학습 내용: 모델이 수렴하지 못함을 확인할 수 있음.

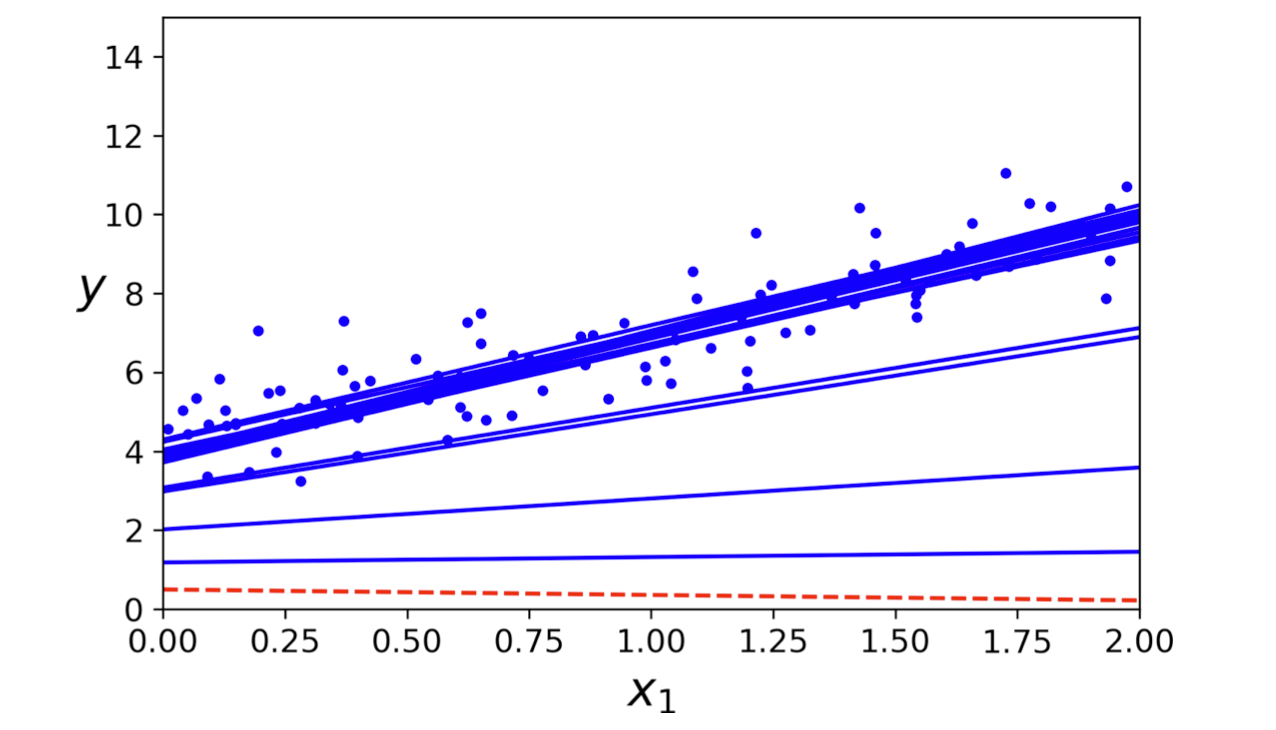
학습 스케줄

• 요동치는 파라미터를 제어하기 위해 학습률을 학습 과정 동안 천천히 줄어들게 만들 수 있음

• 주의사항
  • 학습률이 너무 빨리 줄어들면, 지역 최솟값에 갇힐 수 있음
  • 학습률이 너무 느리게 줄어들면 전역 최솟값에 제대로 수렴하지 못하고 맴돌 수 있음

• 학습 스케줄(learning schedule)
  • 훈련이 지속될 수록 학습률을 조금씩 줄이는 기법
  • 에포크, 훈련 샘플 수, 학습되는 샘플의 인덱스에 따른 학습률 지정

사이킷런의 SGDRegressor

• 경사 하강법 사용

• 사용되는 하이퍼파라미터

  • max_iter=1000: 에포크 수 제한
  • tol=1e-3: 하나의 에포크가 지날 때마다 0.001보다 적게 손실이 줄어들 때까지 훈련.
  • eta0=0.1: 학습 스케줄 함수에 사용되는 매개 변수. 일종의 학습률.
  • penalty=l2: 규제 사용 여부 결정 (추후 설명)

4.2.3 미니배치 경사 하강법

• 장점

  • 배치 크기를 어느 정도 크게 하면 확률적 경사 하강법(SGD) 보다 파라미터의 움직임이 덜 불규칙적이 됨
  • 반면에 배치 경사 하강법보다 빠르게 학습
  • 학습 스케줄 잘 활용하면 최솟값에 수렴함.

• 단점

  • SGD에 비해 지역 최솟값에 수렴할 위험도가 보다 커짐.

경사 하강법 비교

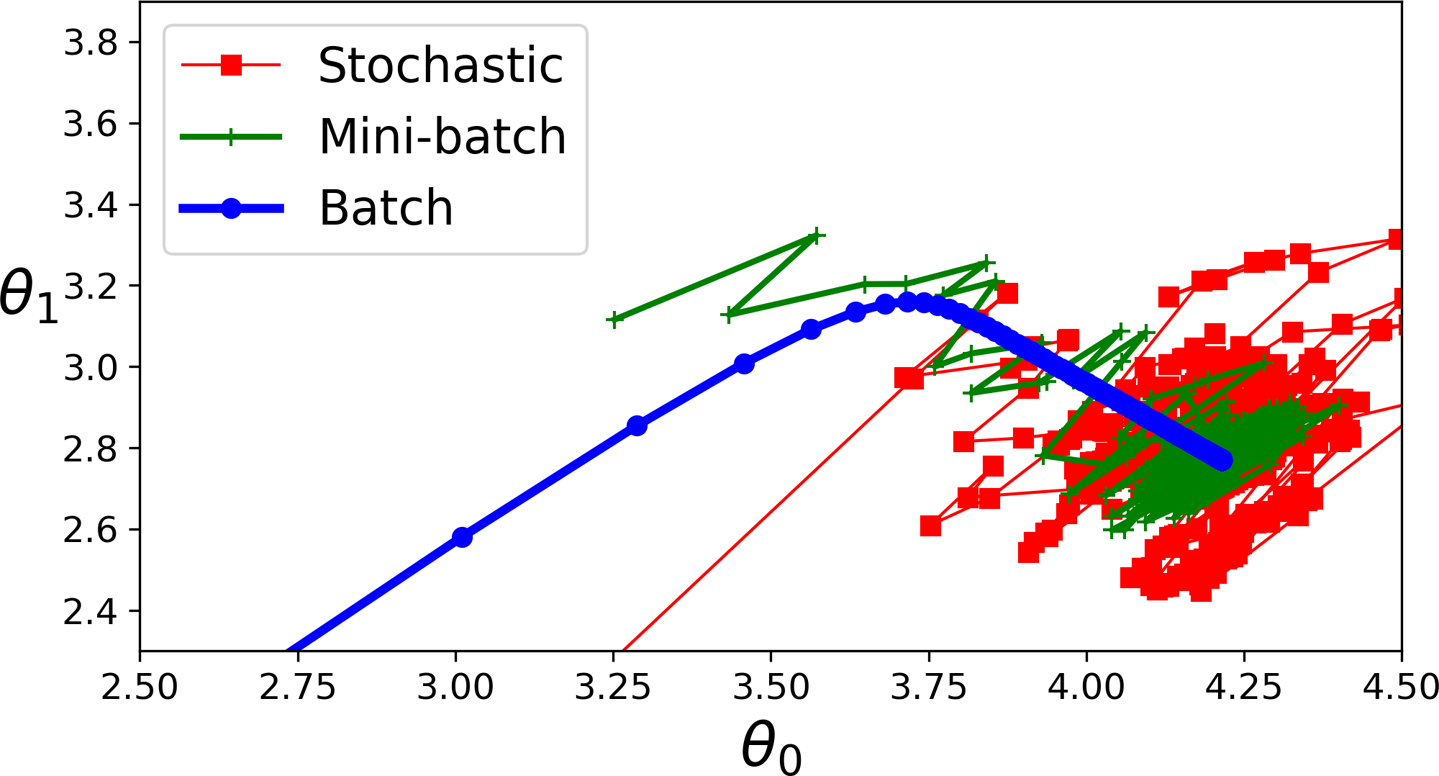
선형 회귀 알고리즘 비교

알고리즘	많은 샘플 수	외부 메모리 학습	많은 특성 수	하이퍼 파라미터 수	스케일 조정	사이킷런 지원
정규방정식	빠름	지원 안됨	느림	0	불필요	지원 없음
SVD	빠름	지원 안됨	느림	0	불필요	LinearRegression
배치 GD	느림	지원 안됨	빠름	2	필요	LogisticRegression
SGD	빠름	지원	빠름	>= 2	필요	SGDRegressor
미니배치 GD	빠름	지원	빠름	>=2	필요	지원 없음

4.3 다항 회귀

• 다항 회귀(polynomial regression)란?
  • 선형 회귀를 이용하여 비선형 데이터를 학습하는 기법
  • 즉, 비선형 데이터를 학습하는 데 선형 모델 사용을 가능하게 함.

• 기본 아이디어
  • 특성들의 조합 활용
  • 특성 변수들의 다항식을 조합 특성으로 추가

선형 회귀 vs. 다항 회귀

선형 회귀: 1차 선형 모델

$$\hat y = \theta_0 + \theta_1\, x_1$$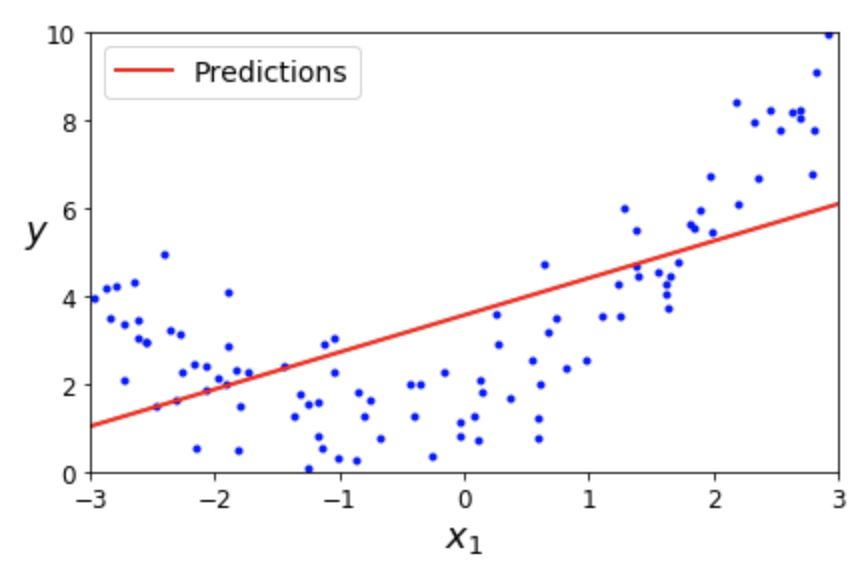

다항 회귀: 2차 다항식 모델

$$\hat y = \theta_0 + \theta_1\, x_1 + \theta_2\, x_1^{2}$$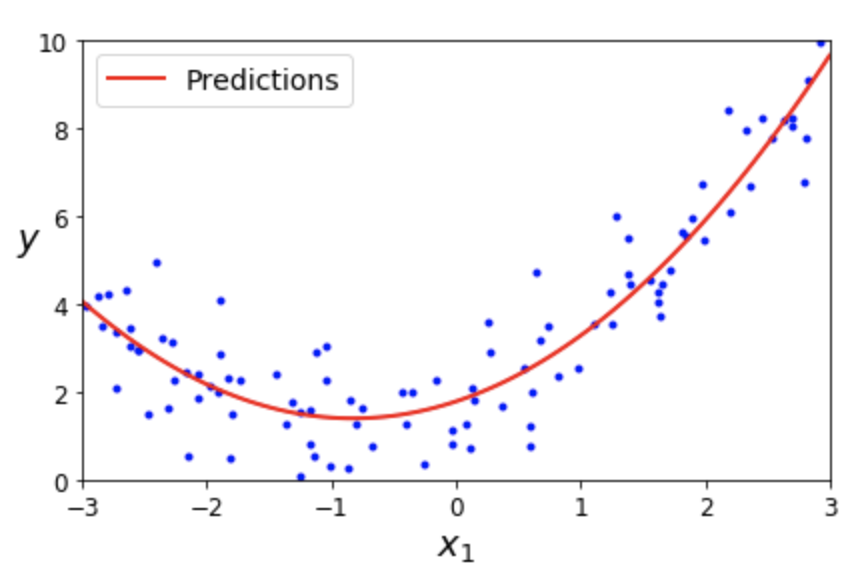

사이킷런의 PolynomialFeatures 변환기

• 주어진 특성들의 거듭제곱과 특성들 사이의 곱셈을 실행하여 특성을 추가하는 기능 제공

• degree=d: 몇 차 다항식을 활용할지 지정하는 하이퍼파라미터

  • 이전 예제: $d=2$으로 지정하여 $x_1^2$에 대한 특성 변수가 추가됨.

• 예제: $n=2, d=3$인 경우에 $(x_1+x_2)^2$과 $(x_1+x_2)^3$의 항목에 해당하는 7개 특성 추가

$$x_1^2,\,\, x_1 x_2,\,\, x_2^2,\,\, x_1^3,\,\, x_1^2 x_2,\,\, x_1 x_2^2,\,\, x_2^3$$

4.4 학습 곡선

과소적합/과대적합 판정

• 예제: 선형 모델, 2차 다항 회귀 모델, 300차 다항 회귀 모델 비교

• 다항 회귀 모델의 차수에 따라 훈련된 모델이 훈련 세트에 과소 또는 과대 적합할 수 있음.

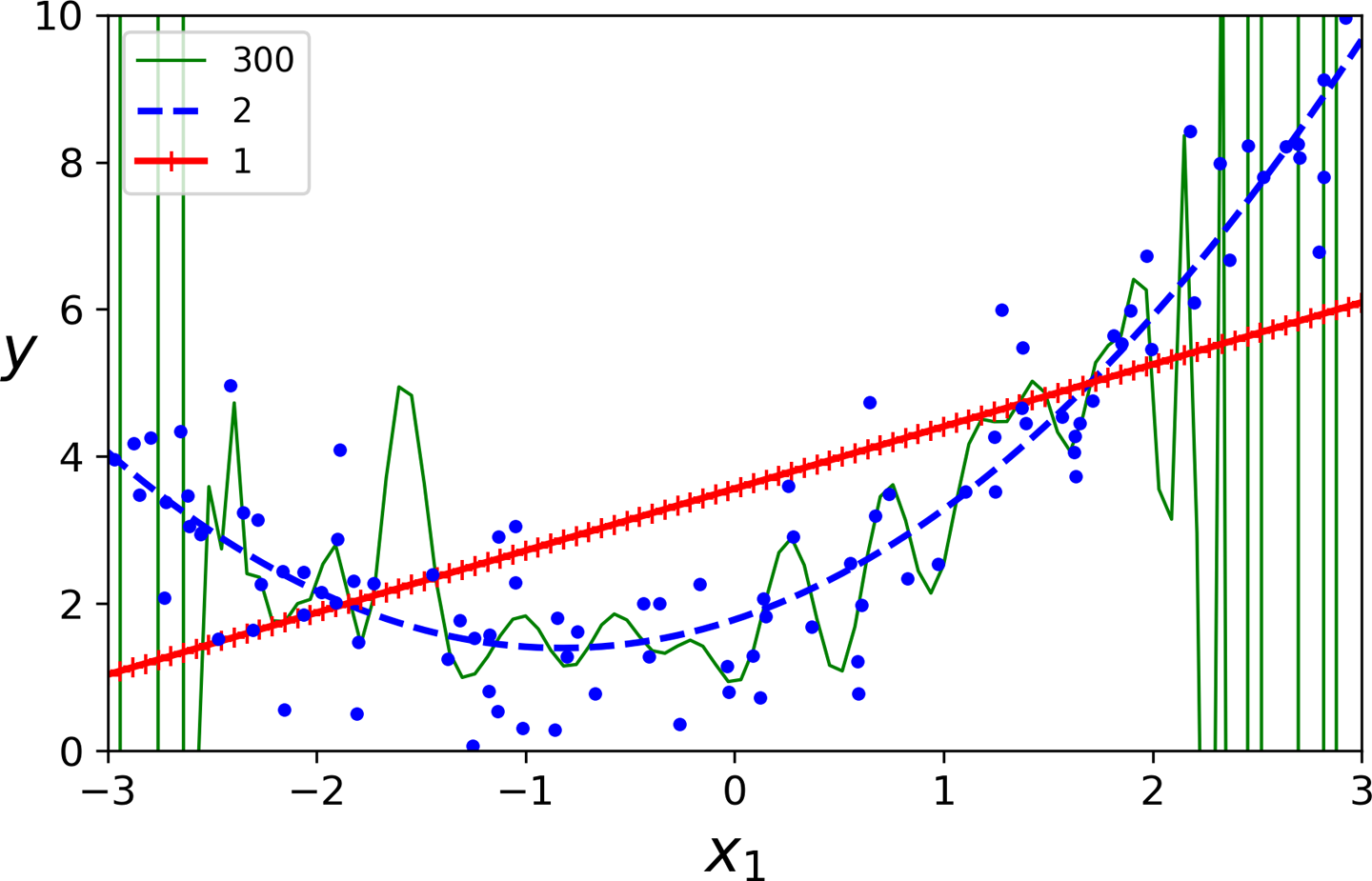
교차 검증 vs. 학습 곡선

• 교차 검증(2장)
  • 과소적합: 훈련 세트와 교차 검증 점수 모두 낮은 경우
  • 과대적합: 훈련 세트에 대한 검증은 우수하지만 교차 검증 점수가 낮은 경우

• 학습 곡선 살피기
  • 학습 곡선: 훈련 세트와 검증 세트에 대한 모델 성능을 비교하는 그래프
  • 학습 곡선의 모양에 따라 과소적합/과대적합 판정 가능

과소적합 모델의 학습 곡선 특징

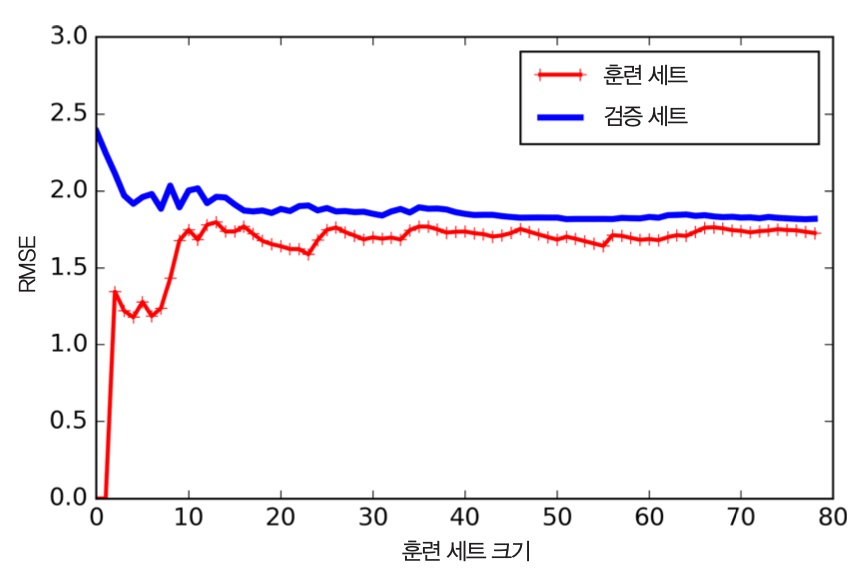
• 훈련 데이터(빨강)에 대한 성능
  • 훈련 세트가 커지면서 RMSE(평균 제곱근 오차)가 커짐
  • 훈련 세트가 어느 정도 커지면 더 이상 RMSE가 변하지 않음

• 검증 데이터(파랑)에 대한 성능
  • 검증 세트에 대한 성능이 훈련 세트에 대한 성능과 거의 비슷해짐

과대적합 모델의 학습 곡선 특징

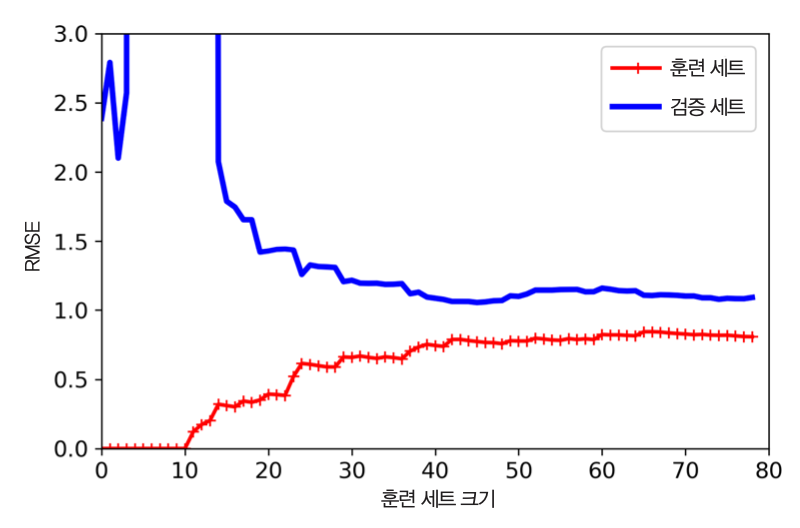
• 훈련 데이터(빨강)에 대한 성능: 훈련 데이터에 대한 평균 제곱근 오차가 매우 낮음.

• 검증 데이터(파랑)에 대한 성능: 훈련 데이터에 대한 성능과 차이가 크게 벌어짐.

• 과대적합 모델 개선법: 훈련 데이터 추가

편향 vs 분산

• 편향(bias)
  • 실제로는 2차원 모델인데 1차원 모델을 사용하는 경우처럼 잘못된 가정으로 인해 발생.
  • 과소적합 발생 가능성 높음.

• 분산(variance)
  • 모델이 훈련 데이터에 민감하게 반응하는 정도
  • 고차 다항 회귀 모델의 경우 분산이 높아질 수 있음.
  • 과대적합 발생 가능성 높음.

• 편향과 분산의 트레이드 오프
  • 복잡한 모델일 수록 편향을 줄어들지만 분산을 커짐.

모델 일반화 오차

• 훈련 후에 새로운 데이터 대한 예측에서 발생하는 오차를 가리키며 세 종류의 오차가 있음.

• 편향

• 분산

• 줄일 수 없는 오차
  • 데이터 자체가 갖고 있는 잡음(noise) 때문에 발생.
  • 잡음을 제거해야 오차를 줄일 수 있음.