3장 분류 (1부)¶

감사의 글¶

자료를 공개한 저자 오렐리앙 제롱과 강의자료를 지원한 한빛아카데미에게 진심어린 감사를 전합니다.

주요내용¶

MNIST

이진 분류기 훈련

분류기 성능 측정

3.1 MNIST¶

MNIST 데이터셋¶

미국 고등학생과 인구조사국 직원들이 손으로 쓴 70,000개의 숫자 이미지로 구성된 데이터셋

사용된 0부터 9까지의 숫자는 각각 28x28= 784크기의 픽셀로 구성된 이미지 데이터
- 2차원 어레이가 아닌 길이가 784인 1차원 어레이로 제공

레이블: 총 70,000개의 사진 샘플이 표현하는 값

문제 정의¶

지도학습: 각 이미지가 담고 있는 숫자가 레이블로 지정됨.

분류: 이미지 데이터를 분석하여 0부터 9까지의 숫자로 분류
- 이미지 그림을 총 10개의 클래스로 분류하는 다중 클래스 분류(multiclass classification) 다항 분류(multinomial classification)라고도 불림

배치 또는 온라인 학습: 둘 다 가능
- 모델에 따라 처리 방법이 다름
  - 확률적 경사하강법(stochastic gradient descent, SGD): 배치와 온라인 학습 모두 지원
  - 랜덤 포레스트 분류기: 배치 학습

훈련 셋과 데이터 셋 나누기¶

MNIST 데이터셋 이미 6:1 분류되어 있음

훈련 세트: 앞쪽 60,000개 이미지

테스트 세트: 나머지 10,000개의 이미지

3.2 이진 분류기 훈련¶

예제: 숫자 5-감지기¶

이미지 샘플이 숫자 5를 표현하는지 여부를 판단하는 이진 분류기

모든 레이블을 0 또는 1로 수정해야 함
- 0: 숫자 5 이외의 수를 가리키는 이미지 레이블
- 1: 숫자 5를 가리키는 이미지 레이블
- 결과: y_train_5

SGD 분류기 활용 학습¶

SGDClassifier(SGD 분류기)
- 확률적 경사 하강법(stochastic gradient descent) 분류기라고 불림.
- 한 번에 하나씩 훈련 샘플 처리 후 파라미터 조정
- 매우 큰 데이터셋 처리에 효율적이며 온라인 학습에도 적합함.

훈련: fit() 메서드 호출

from sklearn.linear_model import SGDClassifier

  sgd_clf = SGDClassifier(max_iter=1000, tol=1e-3, random_state=42)
  sgd_clf.fit(X_train, y_train_5)

3.3 성능 측정¶

성능 측정 세가지 방법¶

교차 검증을 활용한 정확도 측정

정밀도/재현율 조율

AUC 측정

3.3.1 교차 검증을 사용한 정확도 측정¶

2장에서 배운 교차검증 기술을 이용하여 SGD 분류기의 성능을 측정

성능 측정 기준: 정확도

예제: 숫자 5를 표현하는 이미지를 정확하게 예측한 비율. cross_val_score 모델의 scoring="accuracy" 키워드 인자 지정
```
from sklearn.model_selection import cross_val_score

  cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")
```

3.3.2 오차 행렬¶

교차 검증 결과가 95% 이상으로 매우 우수한 것으로 나옴.
- 하지만 무조건 '5 아님'이라고 찍는 분류기도 90%의 정확도를 보임.
- 훈련 세트의 샘플이 불균형적으로 구성되었다면, 정확도를 분류기의 성능 측정 기준으로 사용하는 것은 피해야 함

오차 행렬을 조사하여 분류기의 성능을 다르게 평가할 수 있음

오차 행렬: 클래스별 예측 결과를 정리한 행렬

오차 행렬의 행은 실제 클래스를, 열은 예측된 클래스를 가리킴
- 클래스 A의 샘플이 클래스 B의 샘플로 분류된 횟수를 알고자 하면 A행 B열의 값을 확인

예제: 숫자 5의 이미지 샘플을 3으로 잘못 예측한 횟수를 알고 싶다면?
- 6행 4열, 즉, (6,4) 인덱스에 위치한 값을 확인 (0부터 9까지의 숫자임에 주의)

예제: '숫자 5-감지기'에 대한 오차 행렬은 (2, 2) 모양의 2차원 (넘파이) 어레이로 생성됨.
- 레이블의 값이 0과 1 두 개의 값으로 구성되기 때문

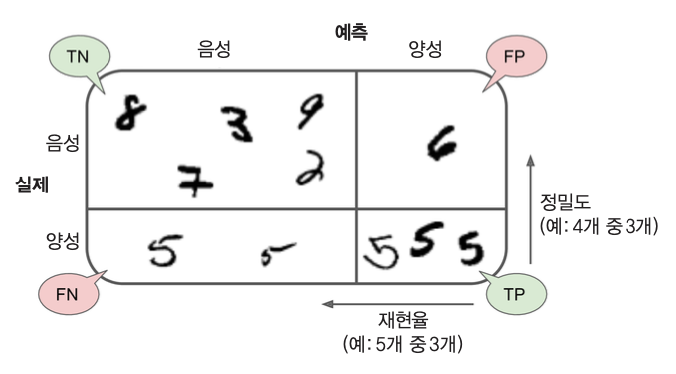
3.3.3 정밀도와 재현율¶

정밀도(precision)¶

책 134쪽의 오차 행렬

  array([[53057, 1522],
         [ 1325, 4096]])

양성 예측의 정확도

여기서는 숫자 5라고 예측된 값들 중에서 진짜로 5인 숫자들의 비율

$$\text{precision} = \frac{TP}{TP+FP} = \frac{4096}{4096 + 1522} = 0.729$$

재현율(recall)¶

정밀도 하나만으로 분류기의 성능을 평가할 수는 없음
- 숫자 5를 가리키는 이미지 중에 숫자 5라고 판명한 비율인 재현율을 고려하지 않기 때문

양성 샘플에 대한 정확도, 즉, 분류기가 정확하게 감지한 양성 샘플의 비율

재현율을 민감도(sensitivity) 또는 참 양성 비율(true positive rate)로도 부름

$$\text{recall} = \frac{TP}{TP+FN} = \frac{4096}{4096 + 1325} = 0.756$$

F₁ 점수¶

정밀도와 재현율의 조화 평균인 F₁ 점수를 이용하여 분류기의 성능을 평가하기도 함.

$$\text{F}_1 = \frac{2}{\frac{1}{\text{정밀도}} + \frac{1}{\text{재현율}}}$$

F₁ 점수가 높을 수록 분류기의 성능을 좋게 평가하지만 경우에 따라 재현율과 정밀도 둘 중의 하나에 높은 가중치를 두어야 할 때가 있음.
- 앞서 정의된 F₁ 점수는 재현율과 정밀도의 중요도가 동일하다고 가정하였음.

정밀도 대 재현율¶

모델 사용의 목적에 따라 정밀도와 재현율의 중요도가 다를 수 있음.

재현율이 보다 중요한 경우: 암 진단 기준
- 정밀도: 양성으로 진단된 경우 중에 실제로도 양성인 경우의 비율
- 재현율: 실제로 양성인 경우 중에서 양성으로 진단하는 경우의 비율

정밀도가 보다 중요한 경우: 아이에게 보여줄 안전한 동영상 선택 기준
- 정밀도: 안전하다고 판단된 동영상 중에서 실제로도 안전한 동영상의 비율
- 재현율: 실제로 좋은 동영상 중에서 좋은 동영상이라고 판단되는 동영상 비율

3.3.4 정밀도/재현율 트레이드오프¶

정밀도와 재현율은 상호 반비례 관계임.

정밀도와 재현율 사이의 적절한 비율을 유지하는 분류기를 찾아야 함.

적절한 결정 임곗값을 지정해야 함.

결정 함수와 결정 임곗값¶

결정 함수(decision function): 분류기가 각 샘플의 점수를 계산할 때 사용

결정 임계값(decision threshold): 결정 함수가 양성 클래스 또는 음성 클래스로 분류하는 데에 사용하는 기준값

임곗값이 커질 수록 정밀도는 올라가지만 재현율은 떨어짐.

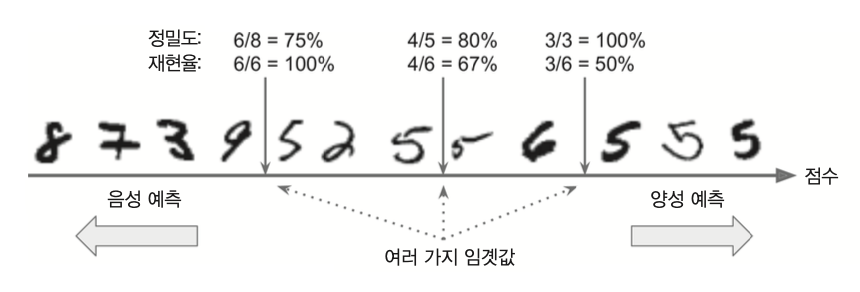
임곗값, 재현율, 정밀도

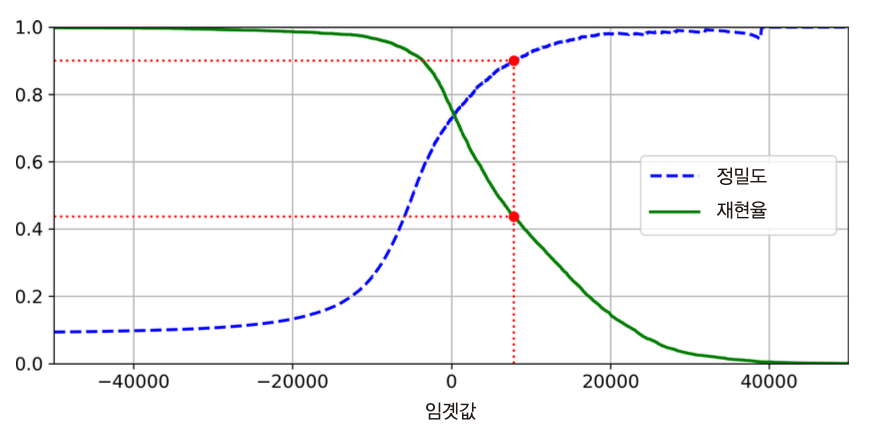
재현율 대 정밀도

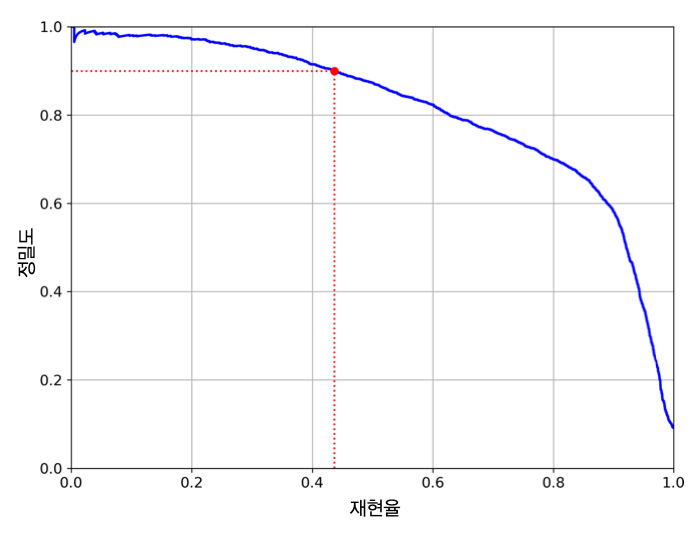
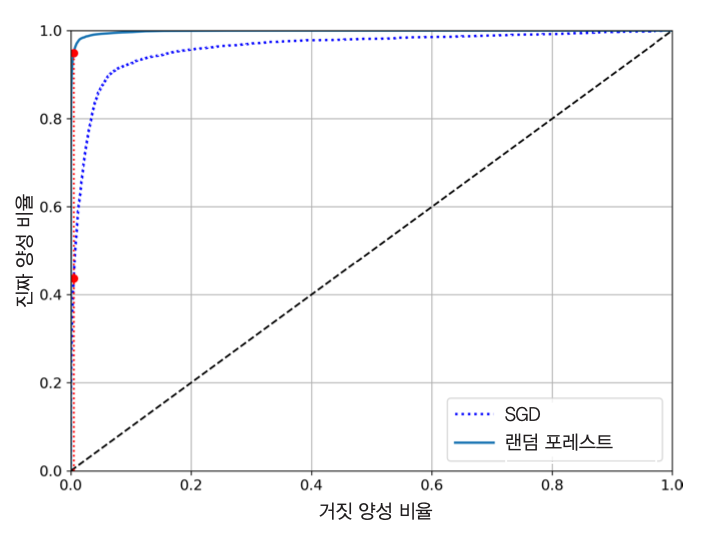
3.3.5 ROC 곡선과 AUC 점수¶

수신기 조작 특성(receiver operating characteristic, ROC) 곡선을 활용하여 이진 분류기의 성능 측정 가능

ROC 곡선: 거짓 양성 비율(false positive rate, FPR)에 대한 참 양성 비율(true positive rate, TPR)의 관계를 나타내는 곡선
- 결정 임곗값에 따른 두 비율의 변화를 곡선으로 보여줌.
- 참 양성 비율: 재현율

거짓 양성 비율: 원래 음성인 샘플 중에서 양성이라고 잘못 분류된 샘플들의 비율. 예를 들어, 5가 아닌 숫자중에서 5로 잘못 예측된 숫자의 비율

$$\text{FPR} = \frac{FP}{FP+TN}$$

TPR 대 FPR

AUC와 분류기 성능¶

재현율(TPR)과 거짓 양성 비율(FPR) 사이에도 서로 상쇄하는 기능이 있다는 것을 확인 가능
- 재현율(TPR)을 높이고자 하면 거짓 양성 비율(FPR)도 함께 증가

따라서 좋은 분류기는 재현율은 높으면서 거짓 양성 비율은 최대한 낮게 유지해야함

ROC 곡선이 y축에 최대한 근접하는 결과가 나오도록 해야함.

AUC(ROC 곡선 아래의 면적)가 1에 가까울 수록 성능이 좋은 분류기로 평가됨.

SGD와 랜덤 포레스트의 AUC 비교