2장 머신러닝 프로젝트 처음부터 끝까지 (1부)¶

감사의 글¶

자료를 공개한 저자 오렐리앙 제롱과 강의자료를 지원한 한빛아카데미에게 진심어린 감사를 전합니다.

주요 내용¶

  • 주택 가격을 예측하는 회귀 작업을 살펴보면서 선형 회귀, 결정 트리, 랜덤 포레스트 등 여러 알고리즘의 기본 사용법 소개
  • 머신러닝 시스템 전체 훈련 과정 살펴보기

2.1 실제 데이터로 작업하기¶

  • 유명한 공개 데이터 저장소
    • UC 얼바인(UC Irvine) 대학교 머신러닝 저장소
    • 캐글(Kaggle) 데이터셋
    • 아마존 AWS 데이터셋
  • 메타 포털(공개 데이터 저장소가 나열)
    • 데이터 포털(Data Portals)
    • 오픈 데이터 모니터(Open Data Monitor)
    • 퀀들(Quandl)
  • 인기 있는 공개 데이터 저장소가 나열되어 있는 다른 페이지
    • 위키백과 머신러닝 데이터셋 목록
    • Quora.com
    • 데이터셋 서브레딧(subreddit)

2.2 큰 그림 보기¶

주어진 데이터¶

  • 미국 캘리포니아 주의 20,640개 지역별 인구조사 데이터
  • 특성 10개: 경도, 위도, 중간 주택 연도, 방의 총 개수, 침실 총 개수, 인구, 가구 수, 중간 소득, 중간 주택 가격, 해안 근접도
  • 목표: 구역별 중간 주택 가격 예측 시스템(모델) 구현하기
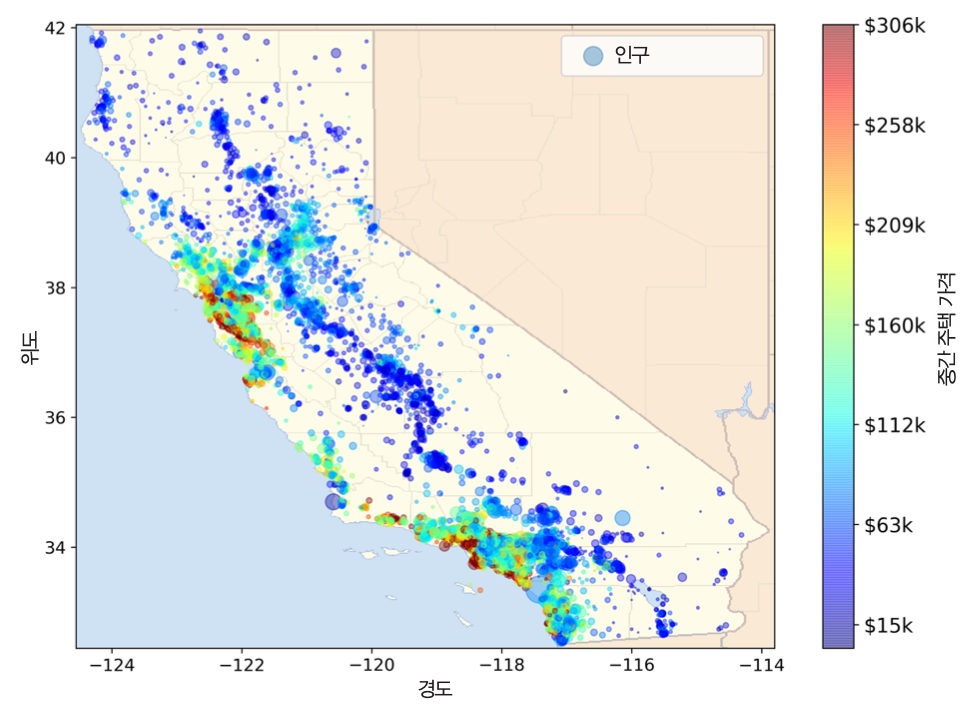
  • 미국 캘리포니아 지도

2.2.1 문제 정의¶

  • 지도 학습(supervised learning)
    • 레이블: 구역별 중간 주택 가격
  • 회귀(regression): 중간 주택 가격 예측
    • 다중 회귀(multiple regression): 여러 특성을 활용한 예측
    • 단변량 회귀(univariate regression): 구역마다 하나의 가격만 예측
  • 배치 학습(batch learning): 빠르게 변하는 데이터에 적응할 필요가 없음

2.2.2 성능 측정 지표 선택¶

사용하는 모델에 따라 모델 성능 측정 기준(norm)을 다르게 선택한다. 선형 회귀 모델의 경우 일반적으로 아래 두 기준 중 하나를 사용한다.

  • 평균 제곱근 오차(RMSE)
  • 평균 절대 오차(MAE)

평균 제곱근 오차(root mean square error, RMSE)¶

  • 유클리디안 노름(Euclidean norm) 또는 $\ell_2$ 노름(norm)으로도 불림
  • 참고: 노름(norm)은 거리 측정 기준을 나타냄.
$$\text{RMSE}(\mathbf X, h) = \sqrt{\frac 1 m \sum_{i=1}^{m} (h(\mathbf x^{(i)}) - y^{(i)})^2}$$
  • 기호 설명
    • $\mathbf X$: 훈련 데이터셋 전체 샘플들의 특성값들로 구성된 행렬, 레이블(타겟) 제외.
    • $\mathbf x^{(i)}$: $i$ 번째 샘플의 전체 특성값 벡터. 레이블(타겟) 제외.
    • $y^{(i)}$: $i$ 번째 샘플의 레이블
    • $h$: 예측 함수
    • $\hat y^{(i)} = h(\mathbf x^{(i)})$: $i$번째 샘플에 대한 예측 값

평균 절대 오차(mean absolute error, MAE)¶

  • MAE는 맨해튼 노름 또는 $\ell_1$ 노름으로도 불림
$$\text{MAE}(\mathbf X, h) = \frac 1 m \sum_{i=1}^{m} \mid h(\mathbf x^{(i)}) - y^{(i)} \mid$$
  • 이상치가 많은 경우 활용
  • $\ell_1$ 노름과 $\ell_2$ 노름을 일반해서 $\ell_n$ 노름을 정의할 수도 있음
  • RMSE가 MAE보다 이상치에 더 민감하지만, 이상치가 많지 않을 경우 일반적으로 RMSE 사용

2.3 데이터 가져오기¶

참고¶

  • 여기서부터 코랩 노트북 함께 참조

2.3.2 데이터 다운로드¶

  • 저자의 깃허브 저장소에 있는 압축파일 다운로드
  • 압축파일을 풀어 csv 파일로 저장

2.3.3 데이터 구조 훑어보기¶

데이터셋 기본 정보 확인¶

  • pandas의 데이터프레임 활용
    • head(), info(), describe(), hist() 등을 사용하여 데이터 구조 훑어보기

head() 메서드 활용 결과¶

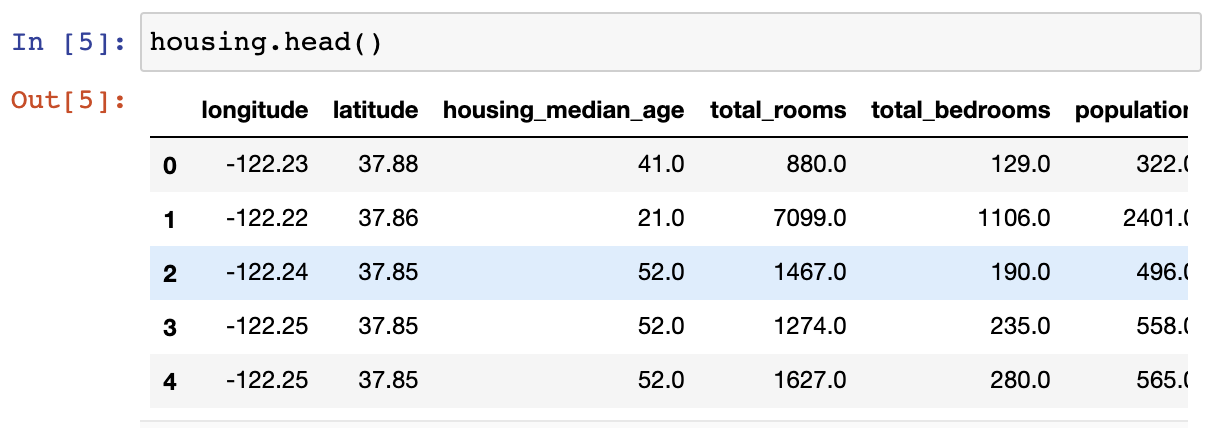
info() 메서드 활용 결과¶

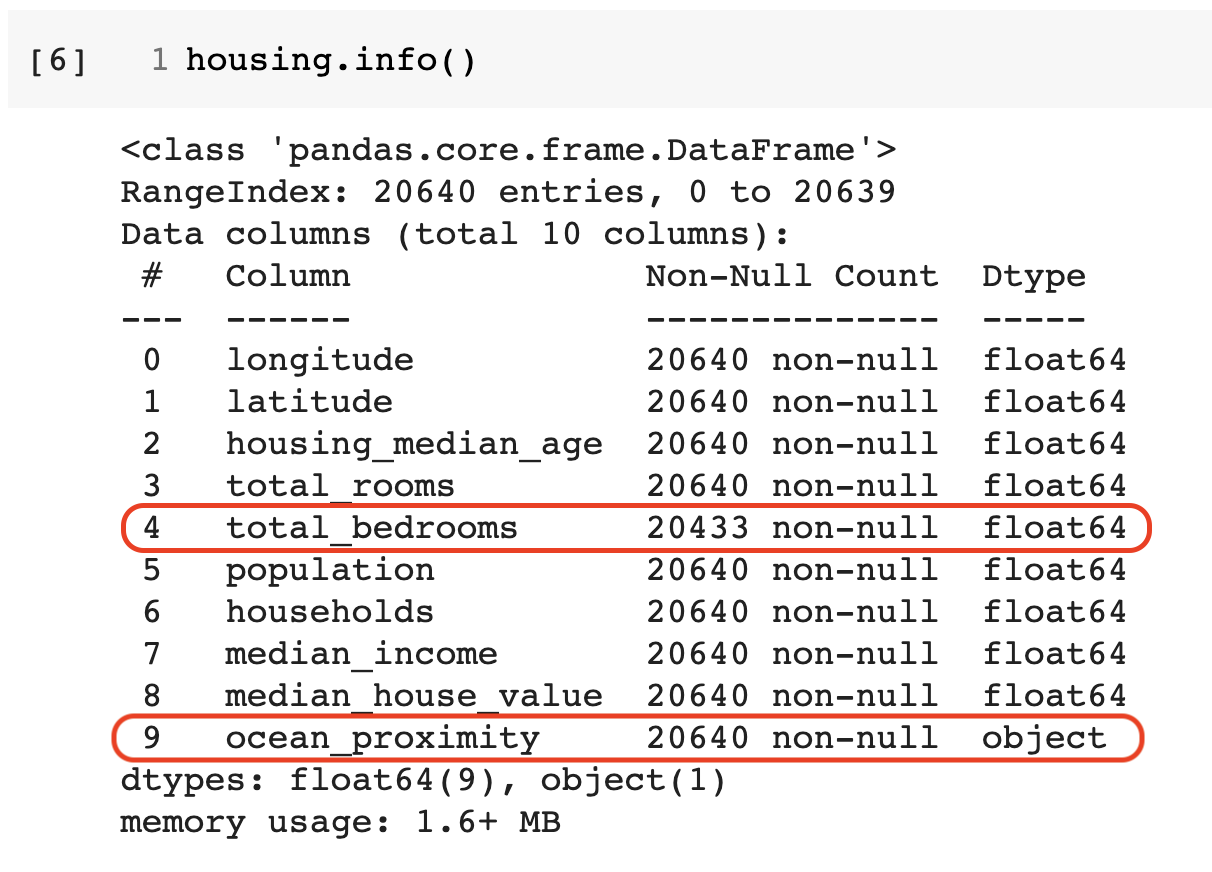
  • 구역 수: 20,640개

  • 구역별로 경도, 위도, 중간 주택 연도, 해안 근접도 등 총 10개의 조사 항목

    • '해안 근접도'는 범주형 특성이고 나머지는 수치형 특성.

  • '방의 총 개수'의 경우 누락된 데이터인 207개의 null 값 존재

범주형 특성 탐색¶

  • '해안 근접도'는 5개의 범주로 구분
특성값 설명
<1H OCEAN 해안에서 1시간 이내
INLAND 내륙
NEAR OCEAN 해안 근처
NEAR BAY 샌프란시스코의 Bay Area 지역
ISLAND 섬

수치형 특성 탐색¶

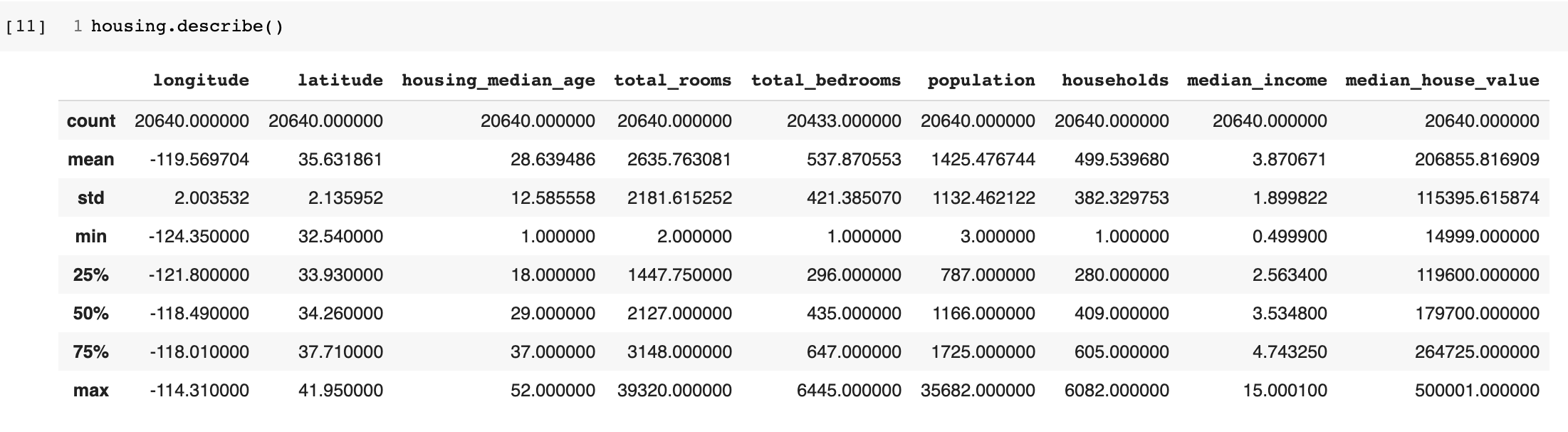
수치형 특성별 히스토그램¶

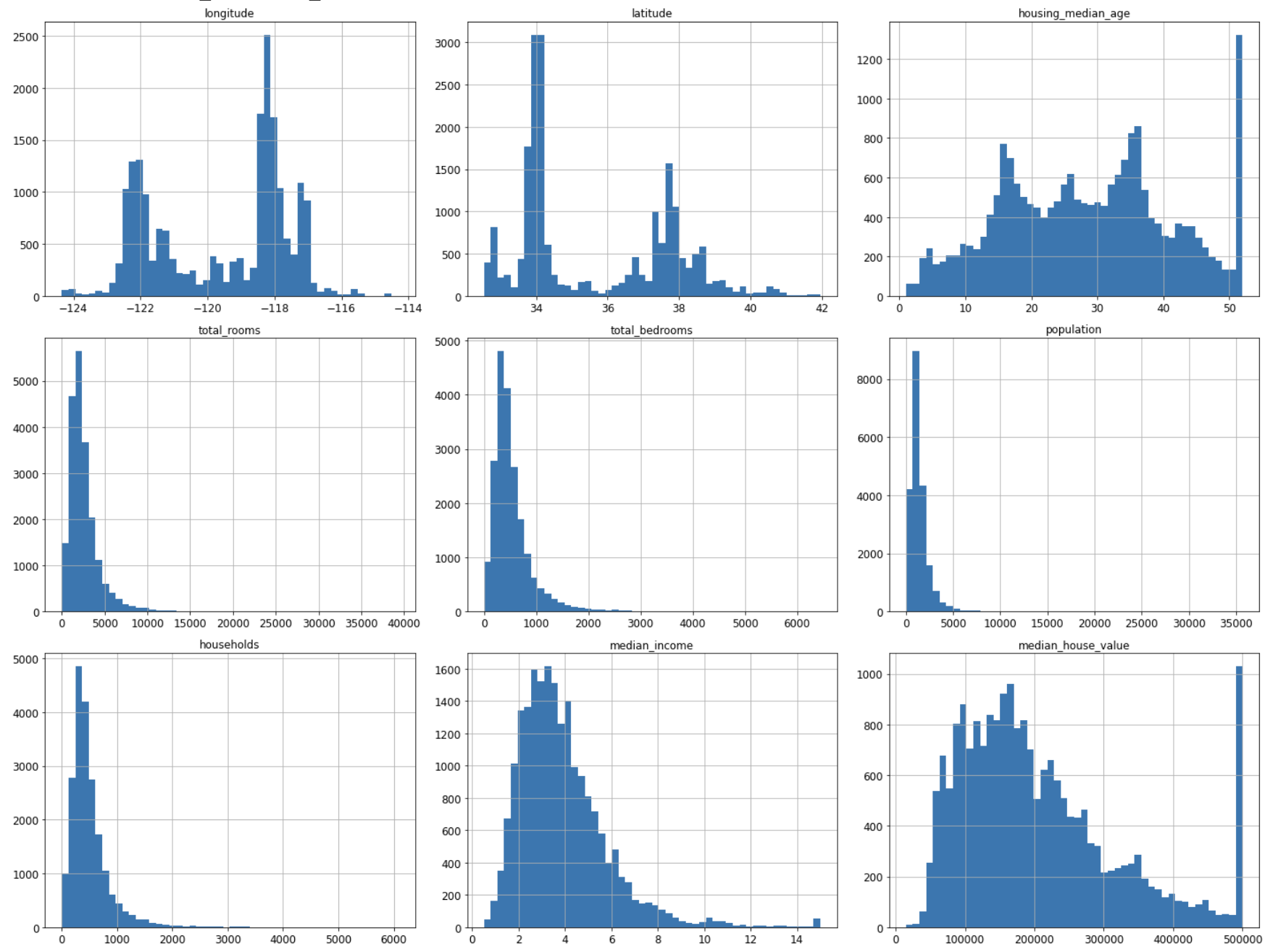
2.3.4 테스트 세트 만들기¶

  • 모델 학습 시작 이전에 준비된 데이터셋을 훈련 세트과 테스트 세트로 구분
    • 테스트 세트 크기: 전체 데이터 셋의 20%
  • 테스트 세트에 포함된 데이터는 미리 분석하지 말 것.
    • 미리 분석 시 데이터 스누핑 편향을 범할 가능성이 높아짐
    • 미리 보면서 알아낸 직관이 학습 모델 설정에 영향을 미칠 수 있음
  • 훈련 세트와 데이터 세트를 구분하는 방식에 따라 결과가 조금씩 달라짐
    • 무작위 샘플링 vs. 계층적 샘플링
  • 여기서는 계층적 샘플링 활용

계층적 샘플링¶

  • 계층: 동질 그룹
    • 예제: 소득별 계층
  • 테스트 세트: 전체 계층을 대표하도록 각 계층별로 적절한 샘플 추출
  • 예제: 소득 범주
    • 계층별로 충분한 크기의 샘플이 포함되도록 지정해야 학습 과정에서 편향이 발생하지 않음
    • 특정 소득 구간에 포함된 샘플이 과하게 적거나 많으면 해당 계층의 중요도가 과대 혹은 과소 평가됨
  • 전체 데이터셋의 중간 소득 히스토그램 활용
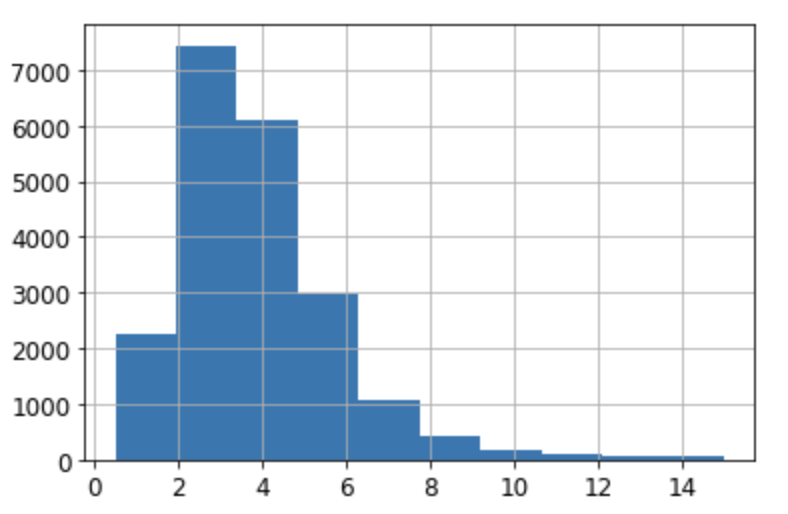
  • 대부분 구역의 중간 소득이 1.5~6.0(15,000~60,000$) 사이

  • 소득 구간을 아래 숫자를 기준으로 5개로 구분

    [0, 1.5, 3.0, 4.6, 6.0, np,inf]

계층 샘플링과 무작위 샘플링 비교¶

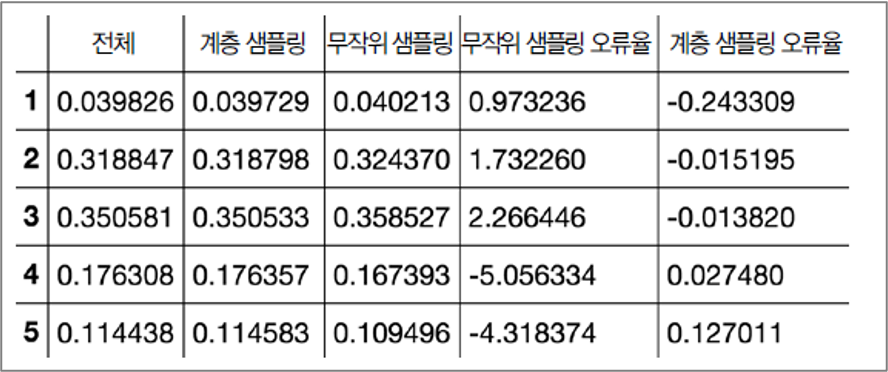
2.4 데이터 이해를 위한 탐색과 시각화¶

주의 사항¶

  • 테스트 세트를 제외한 훈련 세트에 대해서만 시각화를 이용하여 탐색
  • 데이터 스누핑 편향 방지 용도

2.4.1 지리적 데이터 시각화¶

  • 구역이 집결된 지역과 그렇지 않은 지역 구분 가능
  • 샌프란시스코의 베이 에어리어, LA, 샌디에고 등 밀집된 지역 확인 가능
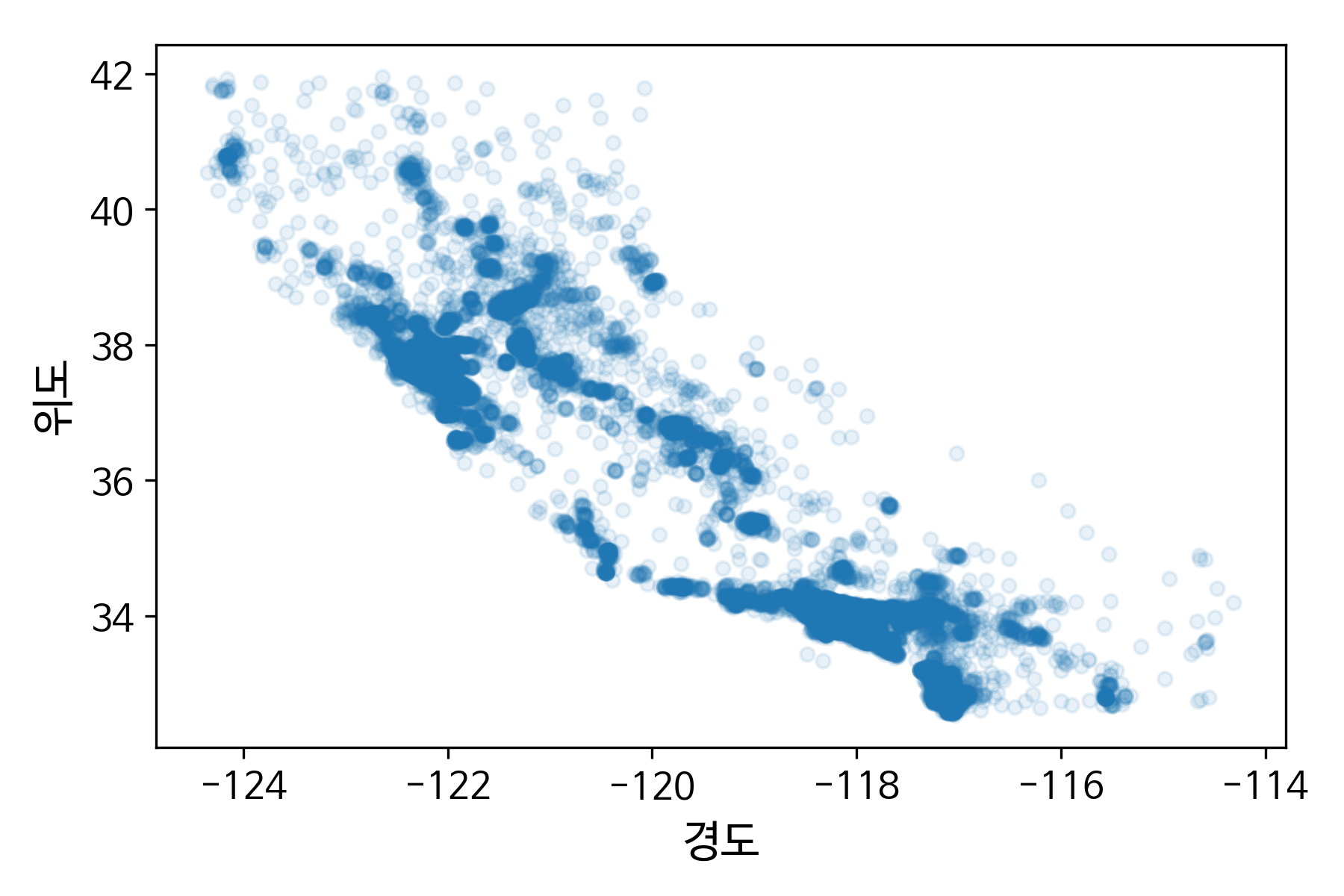
  • 주택 가격이 해안 근접도 또는 인구 밀도와 관련이 큼
  • 해안 근접도: 위치에 따라 다르게 작용
    • 대도시 근처: 해안 근처 주택 가격이 상대적 높음
    • 북부 캘리포니아 지역: 높지 않음

2.4.2 상관관계 조사¶

  • 중간 주택 가격 특성과 다른 특성 사이의 상관관계: 상관계수 활용

상관계수의 특징¶

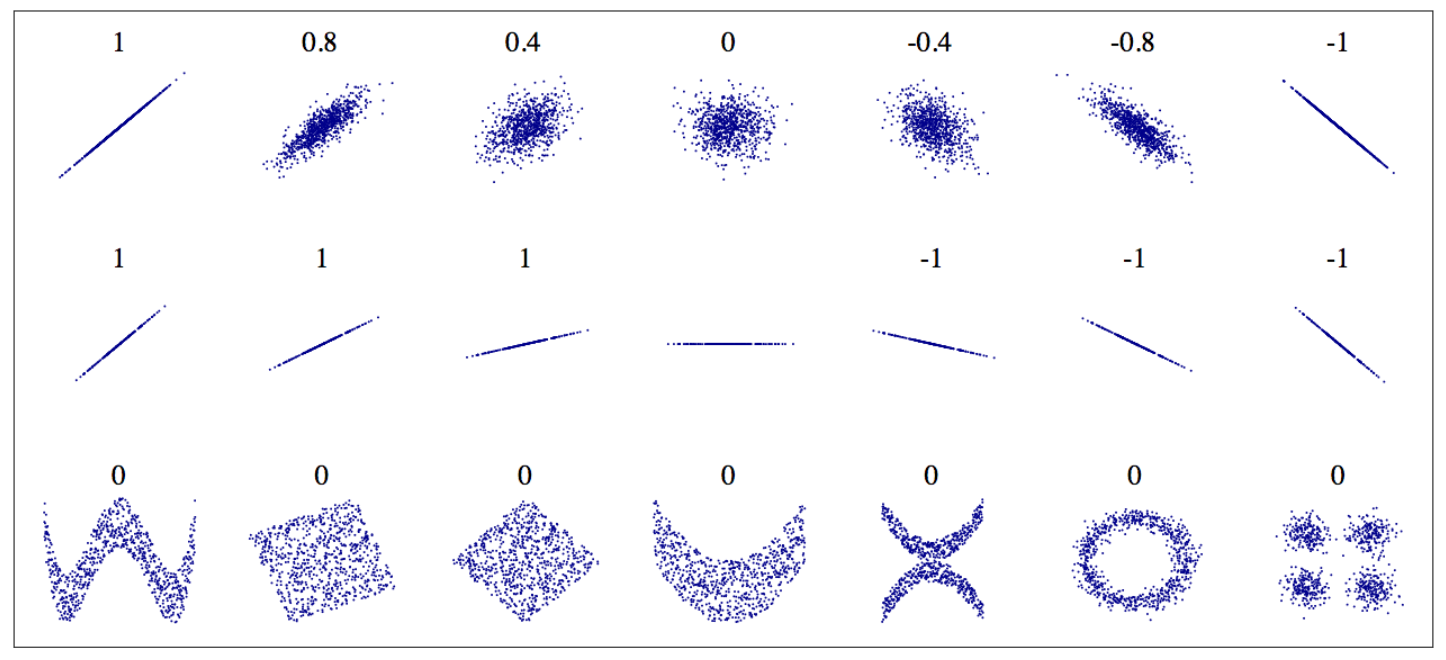
<그림 출처: 위키백과>

  • 상관계수: $[-1, 1]$ 구간의 값

  • 1에 가까울 수록: 강한 양의 선형 상관관계

  • -1에 가까울 수록: 강한 음의 선형 상관관계

  • 0에 가까울 수록: 매우 약한 선형 상관관계

주의사항¶

  • 상관계수가 0에 가까울 때: 선형 관계가 거의 없다는 의미이지, 아무런 관계가 없다는 의미는 아님
  • 상관계수는 기울기와 아무 연관 없음

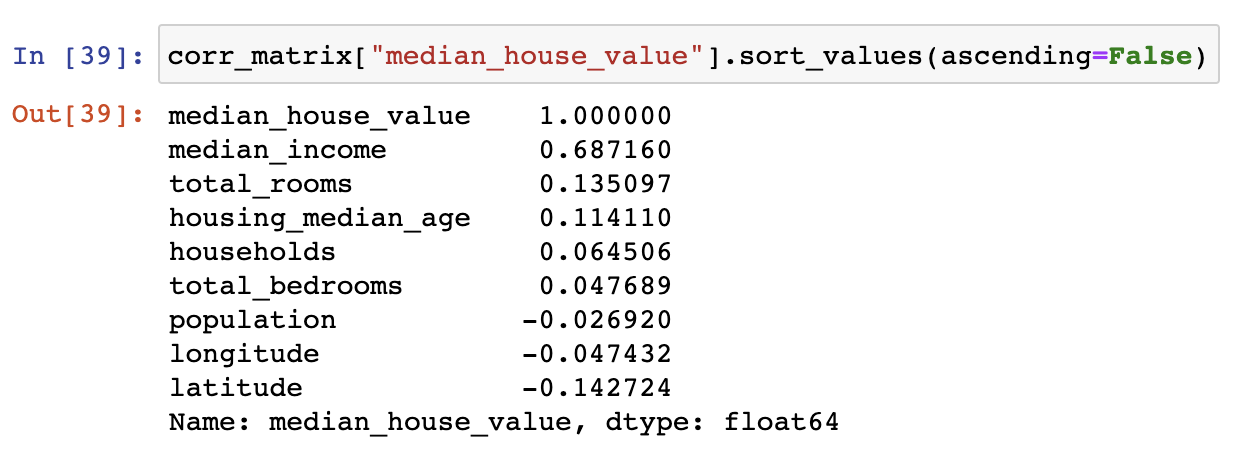
상관계수를 통해 확인할 수 있는 정보¶

  • 중간 주택 가격과 중간 소득의 상관계수가 0.68로 가장 높음
    • 중간 소득이 올라가면 중간 주택 가격도 상승하는 경향이 있음
    • 점들이 너무 넓게 퍼져 있음. 완벽한 선형관계와 거리 멂.
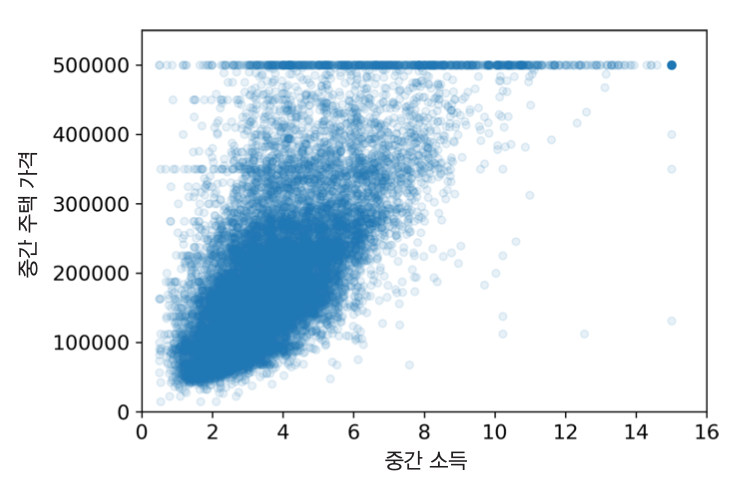
  • 50만 달러 수평선: 가격 제한 결과로 보임
    • 45만, 35만, 28만, 그 아래 정도에서도 수평선 존재. 이유는 알려지지 않음.
    • 이상한 형태를 학습하지 않도록 해당 구역을 제거하는 것이 좋음. (여기서는 그대로 두고 사용)

2.4.3 특성 조합으로 실험¶

  • 구역별 방의 총 개수와 침실의 총 개수 대신 아래 특성이 보다 유용함
    • 가구당 방 개수(rooms for household)
    • 방 하나당 침실 개수(bedrooms for room)
    • 가구당 인원(population per household)
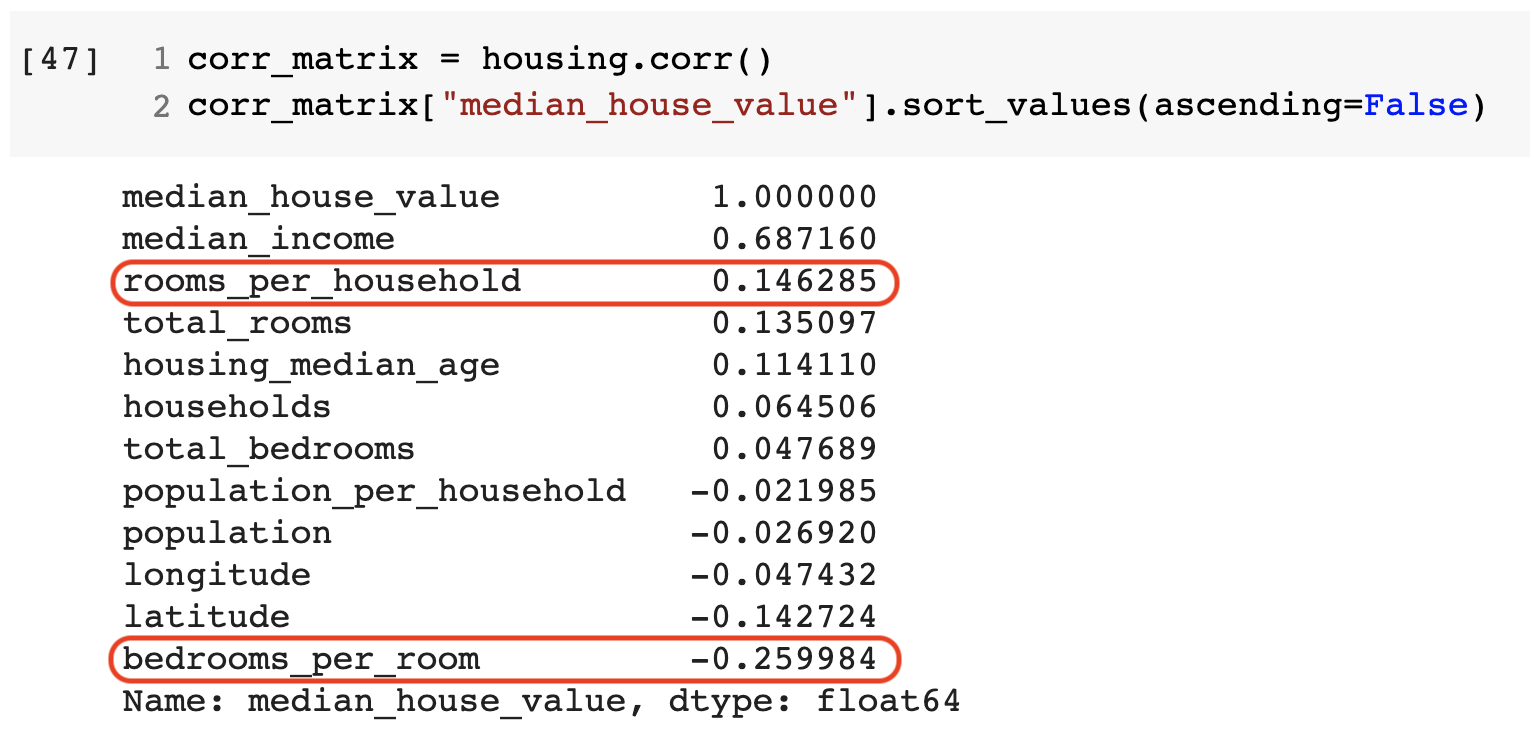
  • 중간 주택 가격과 방 하나당 침실 개수의 연관성 다소 있음
  • 가구당 방 개수의 역할은 여전히 미미함